No caso de termos um sistema com vários corpos, o momento linear do sistema é igual à soma (vetorial) dos momentos lineares de cada corpo. O momento linear do sistema é igual ao momento linear do centro de massa do mesmo.

Por vezes é mais útil considerar esta quantidade do que a velocidade do centro de massa de um sistema de corpos na descrição do seu movimento. De facto, na situação em que a resultante das forças exteriores aplicadas ao sistema é nula, como numa colisão em plano horizontal sem atrito, numa explosão, ou na situação de um sistema com massa variável, o momento linear total conserva-se.¹

Conservação do momento linear total

Consideremos um choque entre dois corpos em translação, com massas \(m_1\) e \(m_2\) , e com velocidades iniciais \(\vec v_1\) e \(\vec v_2\), como está ilustrado na figura seguinte.

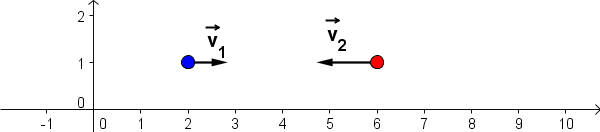
Antes, durante e depois da colisão, a resultante das forças externas que atuam nos corpos é nula. Na colisão apenas intervêm forças internas. Consideremos no que se segue que as forças internas satisfazem a lei do par ação-reação de Newton. Assim, durante a colisão, a força que atua sobre o corpo 1, que é exercida pelo corpo 2, \(\vec F_1\), é simétrica da força que atua no corpo 2 devido à ação do corpo 1. Embora aplicadas em corpos diferentes, a resultante deste par de forças no sistema é nula:

\(\vec F_1 + \vec F_2 = \vec 0\)

Utilizando agora a segunda lei de Newton, pode escrever-se:

\( m_1 \frac{\mathrm{d}\vec v_1}{\mathrm{dt}} + m_2 \frac{\mathrm{d}\vec v_2}{\mathrm{dt}} = \vec 0\)

\(\frac{\mathrm{d}}{\mathrm{dt}}(m_1 \vec v_1 + m_2 \vec v_2) = \vec 0\)

\(\frac{\mathrm{d}}{\mathrm{dt}}(\vec p_1 + \vec p_2) = \vec 0\)

\(\vec p_1 + \vec p_2 = \vec P = constante\)

A última igualdade traduz a conservação do momento linear do sistema. Na condição em que a resultante das forças externas que atuam no sistema é nula, o momento linear do sistema é o mesmo antes e depois da colisão:

\(\vec P = \vec p_1^i + \vec p_2^i = \vec p_1^f + \vec p_2^f\)

É importante salientar que a quantidade de movimento é diretamente proporcional à velocidade a à massa inercial. Imaginemos que temos dois corpos em translação, com velocidades iguais, mas com massas \(m_1\) > \(m_2\). Se quisermos parar os corpos, no mesmo intervalo de tempo, por aplicação de uma força constante na direção do movimento e sentido oposto, o seu módulo deverá ser, para o corpo 1:

\(F_1 = \frac{\mathrm{d}}{\mathrm{dt}}(m_1 v)\)

\(F_1 = m_1 \frac{v_f - v_i}{\Delta t}\)

\(F_1 = m_1 \frac{-v}{\Delta t}\)

e para o corpo 2:

\(F_2 = \frac{\mathrm{d}}{\mathrm{dt}}(m_2 v)\)

\(F_2 = m_2 \frac{v_f - v_i}{\Delta t}\)

\(F_2 = m_2 \frac{-v}{\Delta t}\)

Como \(m_1\) > \(m_2\), temos que \(F_1\) > \(F_2\). É também daqui óbvio que se os dois corpos estivessem inicialmente em repouso, e lhes fosse aplicada uma força constante durante o mesmo intervalo de tempo, o corpo com maior massa atingiria uma velocidade menor.

Sistema de massa variável

Outra ilustração da importância do fator de inércia (massa do corpo) na definição de momento linear, é considerar um sistema que vai perdendo massa ao longo do tempo, mas cuja força exterior resultante seja nula. Consideremos, por exemplo, um foguetão que se move num plano horizontal sem atrito. O foguetão tem inicialmente momento linear total nulo - o foguetão está em repouso - , e massa total M₀. O foguetão é posto em movimento pela expulsão de gases propulsores a uma taxa constante \(R=\frac{\mathrm{d}m}{\mathrm{dt}}\), e ejetados com velocidade \(\vec u\) constante em relação ao foguetão (isto é, tem velocidade \(\vec u - \vec v\) para um observador em repouso). Num instante de tempo t>0, a massa do foguetão é M(t) e do gás expelido é m(t). Como não há forças externas a atuar no sistema gases+foguetão, e considerando o movimento unidimensional, podemos escrever para um instante t>0:

\(\frac{\mathrm{d}}{\mathrm{dt}}(p_{f} + p_{g} )= 0\)

\(\frac{\mathrm{d}}{\mathrm{dt}}(M(t)v - m(t)(u - v)) = 0\)

\(v \frac{\mathrm{d} M(t)}{\mathrm{dt}} + M(t) \frac{\mathrm{d} v}{\mathrm{dt}} - (u - v) \frac{\mathrm{d} m(t)}{\mathrm{dt}} + m(t) \frac{\mathrm{d} v}{\mathrm{dt}} = 0\)

\((M(t)+m(t)) \frac{\mathrm{d}v}{\mathrm{dt}} + v \frac{\mathrm{d} M(t)}{\mathrm{dt}} -(u-v) \frac{\mathrm{d}m(t)}{\mathrm{dt}} = 0\)

Note-se agora que a massa total do sistema M₀ é constante, e M₀ = M(t) + m(t), então \(\frac{\mathrm{d}M(t)}{\mathrm{dt}} = - \frac{\mathrm{d}m(t)}{\mathrm{dt}}\)

\(M_0 \frac{\mathrm{d}v}{\mathrm{dt}} - v \frac{\mathrm{d}m(t)}{\mathrm{dt}} - (u-v) \frac{\mathrm{d}m(t)}{\mathrm{dt}} = 0\)

\(M_0 \frac{\mathrm{d}v}{\mathrm{dt}} - u \frac{\mathrm{d}m(t)}{\mathrm{dt}} = 0\)

\(\frac{\mathrm{d}v}{\mathrm{dt}} = \frac{uR}{M_0}\)

Podemos concluir que a velocidade do foguetão vai aumentar ao longo do tempo, atingindo o valor máximo quando acabar o combustível.

Este problema é resolvido muitas vezes não por conservação do momento linear, mas considerando que os gases propulsores exercem uma força efetiva \(\vec T = R\vec u\) no foguetão, chamada thrust². Chegamos imediatamente à equação:

\(M_0 \frac{\mathrm{d}\vec v}{\mathrm{dt}} = \vec T = R \vec u\)

No entanto, para chegar à expressão desta força é necessário fazer previamente a análise acima da conservação do momento linear.