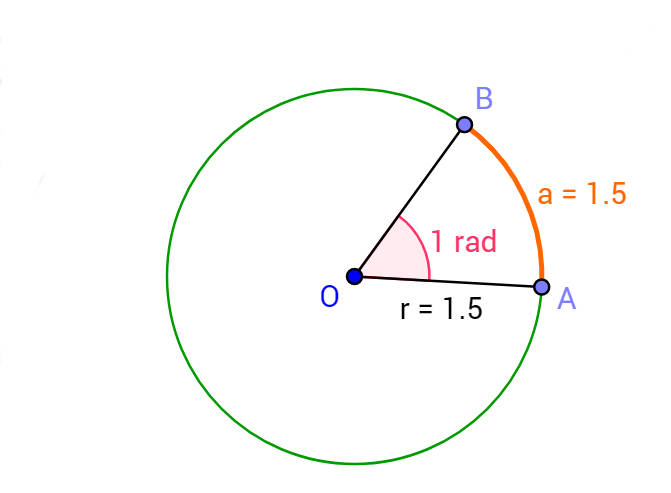
Considere um ângulo ao centro $\displaystyle\theta$, numa circunferência de raio r (veja a figura). Este ângulo ao centro determina um arco $\displaystyle\widehat{AB}$ de comprimento $a$ (medido por exemplo em cm). Por definição, a medida do ângulo $\displaystyle\theta$ em radianos é dada por

$\theta=\displaystyle\frac{\hbox{comprimento do arco}\ \ a}{\hbox{raio} \ \ r}\, rad$

Na FIGURA pode variar os pontos A e B, mudando o arco a. Para um ângulo fixo, pode ainda fazer variar o raio r e constatar que a medida de $\theta$ em radianos se mantem inalterada.

Como converto graus em radianos e vice-versa?

Sabendo que $360^o$ corresponde a $2\pi$ radianos, basta usar uma proporcionalidade direta. Por exemplo:

enquanto que:

isto é:

$45º=\displaystyle\frac{\pi}{4}\,\hbox{rad}, \ \ \ \ \displaystyle\frac{\pi}{6}\,\hbox{rad}=30^o$

Quais as vantagens de usar a medida de ângulos em radianos?

A medida em radianos é adimensional, isto é, não depende da unidade de medida com a qual se medem comprimentos de arco. Recorde que radiano define-se através do quociente entre dois comprimentos - o de um arco e o de um raio de uma circunferência. É indiferente a medida com a qual se medem estes comprimentos. Pode ser em mm, cm, metros, etc.

Em geral, os matemáticos, os físicos, etc., preferem usar a medida dos ângulos em radianos, pois as fórmulas do Cálculo são mais simples quando a variável independente x nas funções trigonométricas tais como $\sin x$, $\cos x$, etc. é expressa em radianos. Por exemplo, só quando x é expresso em radianos é que a derivada da função $\sin x$ é $\cos x$, a derivada do $\cos x$ é -$\sin x$, etc. (ver derivadas das funções trigonométricas).

Como, por exemplo, $\sin x$ é adimensional e $x$ também o é (quando medido em radianos) podemos comparar $\sin x$ com $x$. De facto, para ângulos muito pequenos (perto de 0), $\sin x$ é aproximadamente igual a $x$. Uma melhor aproximação para $\sin x$ é $x-\displaystyle\frac{x^3}{6}$, sendo o erro inferior a $\displaystyle\frac{x^5}{120}$.

Atenção. Erros frequentes

• um erro grave é dizer que $\sin \alpha$ é aproximadamente igual a $\alpha$, mesmo para valores de $\alpha$ muito pequenos, se medimos $\alpha$ em graus.

• outro erro grave é, por exemplo, afirmar que:

$\cos\alpha=\cos(\alpha+2n\pi),\, \forall n\in \mathbb{Z}$

se medimos $\alpha$ em graus. De facto, no segundo membro estamos a somar o valor de um ângulo em graus, $\alpha$, com o valor de um ângulo em radianos, $2n\pi$, o que é absurdo, e torna falsa a igualdade.

• Tenha pois em atenção que em todas as fórmulas trigonométricas que usar, todos os ângulos envolvidos têm obrigatoriamente de estar medidos na mesma unidade (graus, radianos, ou qualquer outra)