Loxodrómias e Espirais – I
📧
- CMAF_IO/ Universidade de Lisboa
Referência Rodrigues, J.F., (2017) Loxodrómias e Espirais – I, Rev. Ciência Elem., V5(2):022
DOI http://doi.org/10.24927/rce2017.022
Palavras-chave Loxodrómia; Loxodrómica; Espiral; Terra; Viagem; Navegação; Cartografia; Astronomia;
Resumo
Na época dos descobrimentos, a expansão europeia e as navegações oceânicas suscitaram novas questões científicas que colocaram aos matemáticos novos problemas geométricos, em particular na navegação, na cartografia e na astronomia. Um dos problemas mais interessantes resultou da necessidade de compreender as linhas de rumo, mais tarde também chamadas linhas loxodrómicas ou loxodrómias.

O primeiro cientista a referir essas curvas sobre o globo e a deduzir a sua forma em espiral que se aproximam dos polos, sem nunca os atingir, foi Pedro Nunes (1502-1578) no “Tratado em defesa da carta de marear”, que integra o seu “Tratado da Sphera” redigido em português e publicado em Lisboa em 15371.
Até quase meados do século XVI, a diferença entre navegar com o leme fixo e segundo um rumo constante não era evidente para os marinheiros, facto que levantou dúvidas e erros na navegação oceânica. O matemático e cosmógrafo Pedro Nunes foi o primeiro a identificar e escrever sobre as linhas de rumo2 que resultam de manter a navegação com o azimute constante, ou seja, fazendo sempre o mesmo ângulo com o Norte geográfico. Nunes distinguiu claramente essas linhas dos círculos máximos, ou ortodrómias, que são as rotas descritas na navegação sem alteração de direção, ou seja, “a direito” sobre a esfera. Assim, enquanto que a loxodrómia é uma linha que cruza todos os meridianos segundo um ângulo — o azimute — constante, a ortodrómia descreve a distância mais curta entre dois pontos numa superfície esférica e é, portanto, a uma linha geodésica sobre o globo. Estas curvas apenas coincidem no caso limite de azimute a 0° , quando são meridianos. Nos casos dos rumos com azimute a 90° as loxodrómias correspondem aos paralelos, exceto o equador que também é uma ortodrómia.

Através da aplicação interativa LOXODRÓMIAS E ESPIRAIS, Loxo, podemos traçar virtualmente linhas de rumo na superfície esférica da Terra, escolhendo um azimute partindo de Lisboa ou comparando as rotas entre duas cidades, escolhidas numa lista, ou entre dois quaisquer pontos no globo a partir das suas latitudes e longitudes.
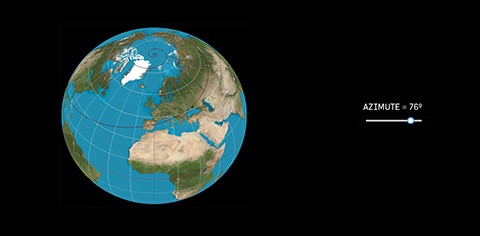
A aplicação Loxo através de um cursor permite selecionar um azimute e produzir loxodrómias como a da figura 3, que corresponde a um ângulo de 76° com o polo Norte e passa por Lisboa. Também permite, como por exemplo na figura 4, verificar que um avião que voe entre Lisboa e Macau seguindo uma linha de rumo percorre mais 852 Km, num total de 11862Km, do que se seguir o trajeto mínimo do círculo máximo que liga as duas cidades.
A primeira versão da Loxo esteve exposta numa exposição promovida pela Sociedade Europeia de Matemática na UNESCO em Paris, em abril de 2013, por ocasião do ano dedicado à Matemática do Planeta Terra e resultou de uma iniciativa do Centro de Matemática e Aplicações Fundamentais da Faculdade de Ciências da Universidade de Lisboa. A atual versão está disponível em http://formas-formulas.fc.ul.pt/interactive/loxo/pt/index_pt.html.

Referências
- 1 Nunes, P, Tratado da Sphera, Lisboa, 1537, Biblioteca Nacional de Portugal http://purl.pt/14445 Reedição, com comentários, pela Academia de Ciências de Lisboa—Fundação Calouste Gulbenkian, Lisboa, 2002.
- 2 Queirós, JP, Pedro Nunes e as Linhas de Rumo, Gazeta de Matemática, 143 (2002), 42-47.
- 3 José Francisco Rodrigues, Alguns aspetos matemáticos do planeta Terra, in “Matemática do Planeta Terra”, editado por F.P.Costa, J.Buescu, J.T.Pinto, IST Press, Lisboa, 2013.
Este artigo já foi visualizado 7398 vezes.



