O desenvolvimento da topografia foi especialmente importante no Egito, pois, após cada cheia do Nilo era necessário restaurar os limites dos terrenos⁵.

Richard Talbert⁵ destaca a existência de dois procedimentos opostos no levantamento topográfico. Um envolve medir uma certa parte da superfície da terra, anotar elementos artificiais sobre ela e registar o resultado num mapa ou plano desenhado a uma escala adequada. O outro, que o autor designa como “traçado”, é o processo inverso: o posicionamento das características pretendidas, limites, edifícios ou obras de engenharia no solo, na posição correta e pretendida. Um agrimensor que pretenda construir, por exemplo, aquedutos ou vias férreas, terá que realizar os dois procedimentos. Primeiro tem que registar a forma do terreno e depois, com essa informação, decidir o melhor percurso e marcá-lo no terreno.

Da necessidade de efetuar medições de terras, nasceu a Geometria grega, e um elemento importante desta Geometria era o estudo dos triângulos e das respetivas semelhanças. Lucio Russo, no seu livro The Forgotten Revolution, afirma⁴: “Heródoto atribui aos egípcios a introdução da Geometria, no sentido original da medição do terreno, e especifica que esta surgiu da necessidade de estimar, para efeitos fiscais, a quantidade de parcelas de terreno que foram corroídos pelo Nilo. Quando a Geometria grega se lançou no seu espetacular curso de desenvolvimento, as suas aplicações concretas, tais como a agrimensura e a topografia, foram reclassificadas sob a rubrica de geodesia. Infelizmente, existe escassa documentação direta sobre a evolução destas técnicas desde a fase empírica, comum a muitas civilizações antigas, até à topografia e cartografia baseadas na ciência helenística”.

O desenvolvimento de uma teoria de topografia mais sofisticada e de instrumentos mais versáteis apareceu no início do século III a.C.⁵ aquando da criação da biblioteca e do museu em Alexandria. Os instrumentos de levantamento topográfico começaram a basearem-se na teoria científica que foi sendo alimentada a partir da experiência prática. O conhecimento sobre a topografia Grega advém de quatro tratados técnicos, mas apenas o de Heron de Alexandria, A Dioptra, do século I d.C. está quase completo. Dos outros, existem fragmentos de manuais anónimos, que se pensam ser dos séculos III e II a.C. e que foram encontrados posteriormente em obras de autores, como Julius Africanus (Anonymus Byzantinus) e al-Karaji². O conteúdo consiste em exercícios práticos acompanhados de diagramas geométricos.

Etimologicamente, a palavra dioptra significa algo para ver através. Para o levantamento topográfico, supõe-se que tenha começado por ser um tubo de visão estreito suspenso horizontalmente por fios ou correntes. Segundo Richard Talbert⁵, é possível que tenha sido adotada pelo Gregos no século VI a.C. mas concebida pela primeira vez na Pérsia para manter o alinhamento e a inclinação ao construir qanats, túneis de captação de água. Já no final do século III a.C., o tubo evoluiu para a alidade — uma barra onde, em cada extremidade, existiam pínulas ou palhetas que serviam de miras. Como era difícil alinhar o buraco com o alvo, adicionaram fendas estreitas para facilitar a visão.

Como já referido, o manuscrito que fala sobre topografia e de um dos instrumentos usados por ela é a A Dioptra. Ainda existem exemplares deste manuscrito e podem ser encontrados, um na Biblioteca Real de Viena, outro na Biblioteca da Universidade de Estrasburgo e outro na Biblioteca Nacional de Paris¹. Segundo Papadopoulos³, a obra começa com uma introdução à “ciência da dioptra” e descreve o instrumento como combinação de teodolito e nível de água. Heron apresenta nesta obra todos os trabalhos anteriores sobre o tema mas rapidamente os dispensa e dá instruções sobre como construir uma dioptra e como utilizá-la. Apesar de não haver conhecimento da existência de um exemplar físico da dioptra feito na antiguidade, vários autores fizeram uma interpretação do que foi dito por Heron propondo uma reconstrução e inserindo elementos básicos que lhes era úteis, ou seja, diferiam em pequenos detalhes. Segundo Gallo¹, desde o século XIX vários autores têm vindo a apresentar propostas, nomeadamente, Venturi, em 1814, Vincent, em 1858 (FIGURA 1A)) e Schöne, em 1899, voltando a aprofundar o assunto em 1903 (FIGURA 1B)). Mais tarde, surgem novas propostas de Drachmann em 1935, 1954 e 1968, a que se segue Adam, em 1982².

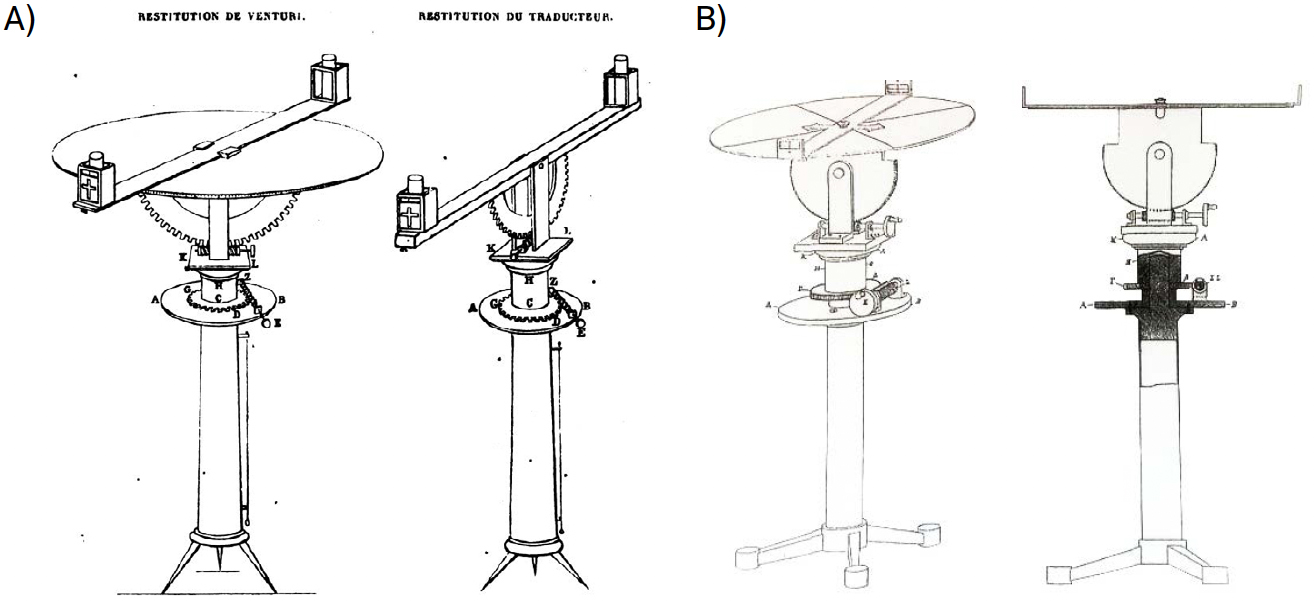
Na obra de Richard Talbert⁵ podemos ler a descrição de uma experiência de reconstrução de uma dioptra padrão com um disco de madeira com 60 cm de diâmetro (FIGURA 2) e, uma vez que as fontes são completas, o autor descreve-a como uma reconstrução que está próxima da verdade. Funciona tanto no plano horizontal como no plano vertical.

Quando está montada horizontalmente sobre um tripé, com a ajuda de uma junta giratória, é usada para projetar linhas retas em qualquer direção, para marcar o solo e, segundo Richard Talbert, também pode ser usada para traçar retas perpendiculares a retas já traçadas por meio de diâmetros em ângulo reto inscritos no disco. Ainda, segundo o autor, um quarto da borda é graduado em graus e foi usado para observações celestes, mas não para levantamentos terrestres.

No seu nível mais básico, o uso da dioptra consiste em traçar ângulos retos, projetar linhas pela mira através da alidade em ambas as direções e construir triângulos semelhantes a outros triângulos já construídos.

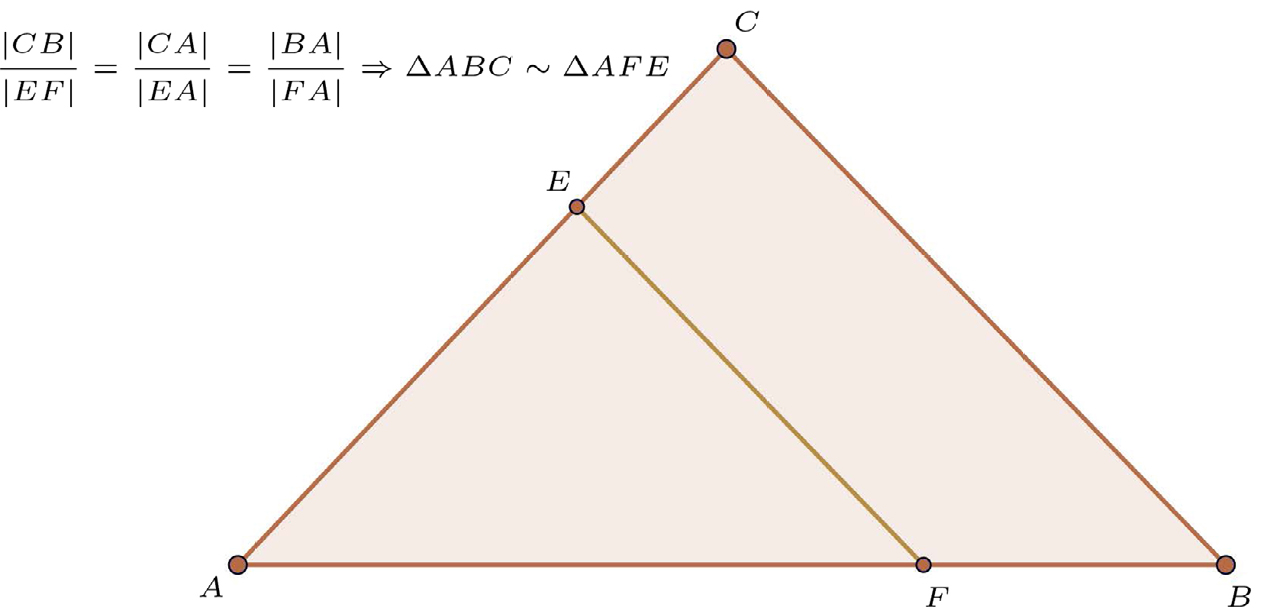
Sabe-se que, se uma reta é paralela a um dos lados de um triângulo e intercepta os outros dois lados em pontos distintos do vértice, então o triângulo que ela determina é semelhante ao primeiro (FIGURA 3). Assim, se dois triângulos têm lados correspondentes proporcionais, então eles são semelhantes — critério LLL. Este resultado será usado diversas vezes nos exemplos que serão vistos à frente.

Os exemplos do uso da dioptra, especialmente os de Heron, são em levantamentos de terras, obras de Engenharia e ainda mapeamento. Por exemplo, na guerra, o uso da dioptra é fundamental e típico. Um exército em marcha pode ver-se obrigado à necessidade de construir uma ponte se encontrarem um rio que lhes impede a passagem.

Calcular a distância de um ponto de uma das margens de um rio a um ponto da margem oposta

Podemos ver uma aplicação da dioptra para calcular a distância de um ponto de uma das margens de um rio a um ponto da margem oposta. Na FIGURA 4 consideramos que \(CD\) e \(MN\) são as margens de um rio. Posiciona-se a dioptra na margem \(MN\) no ponto A e vira-se a alidade até que o ponto \(N\), na margem \(MN\), seja visível através dela. Roda-se a alidade e escolhe-se uma marca, que vamos designar por \(B\), do outro lado do rio, na margem \(CD\), de forma que seja vista através da alidade e que \(AB\) forme um ângulo reto com \(AN\). Para simplificar, o autor² supõe que as margens sejam paralelas. Assim, AB é perpendicular a ambas as margens do rio e será considera a largura do rio.

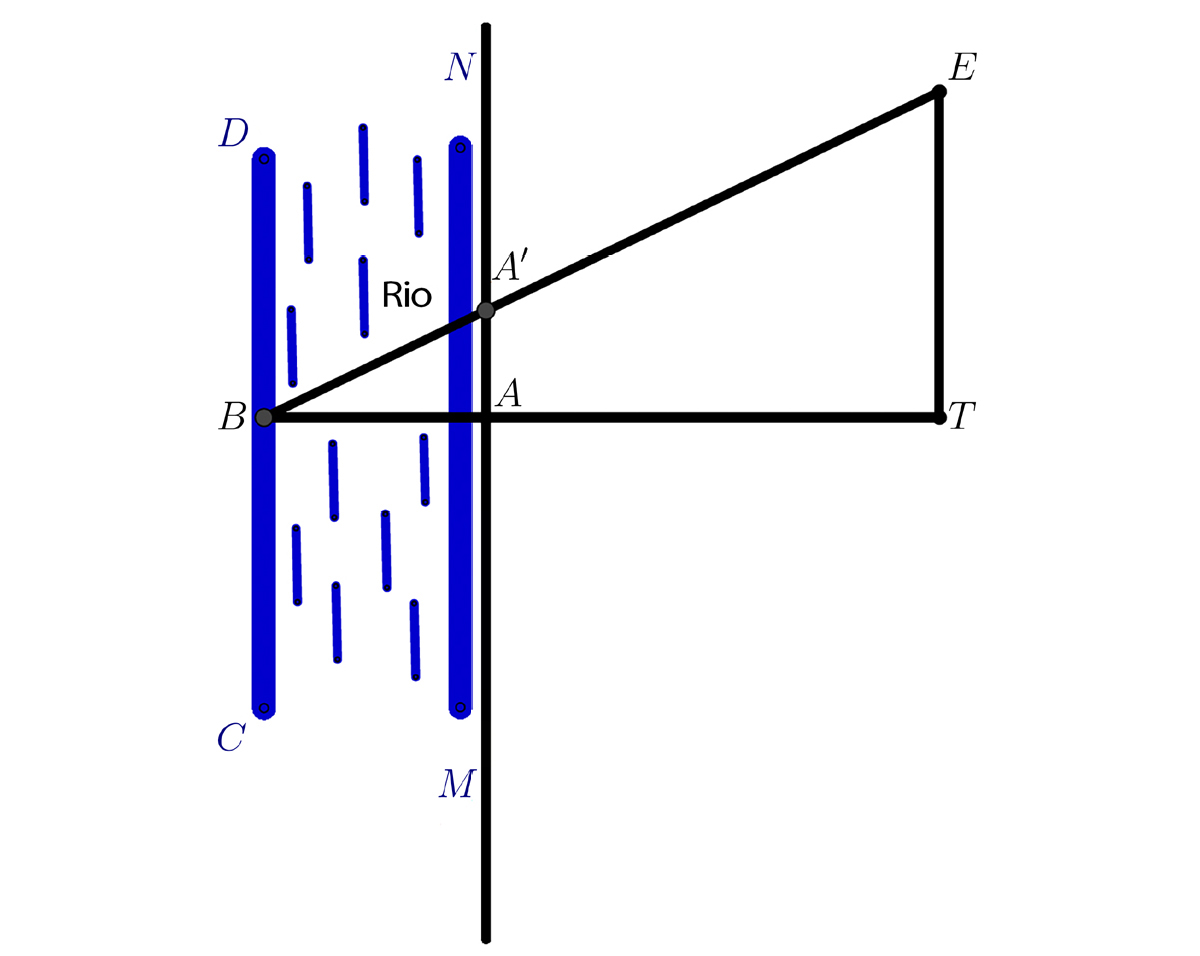
Para proceder à descoberta da distância horizontal de \(A\) a \(B\), ainda com o auxílio da dioptra, temos o ponto \(A\) junto a nós e o ponto \(B\) afastado. Posicionando a dioptra no ponto \(A\), roda-se a alidade até que o ponto \(B\) seja avistado. Dá-se a volta para o outro lado da alidade, ajustando o plano de visão se necessário e, sem mover mais nada, marca-se o ponto \(T\), que se encontra do nosso lado e no alinhamento de \(A\) e \(B\). Depois, com o auxílio da dioptra, traça-se um segmento de reta \(TE\) perpendicular a \(BT\). Move-se a dioptra para o ponto \(E\) e ajusta-se a alidade de forma a visualizar \(B\) e na interseção de \(BE\) com a linha perpendicular a \(AT\) que passa por \(A\) marcamos o ponto \(A′\). Desta forma, estamos perante dois triângulos retângulos, \(BAA′\) e \(BTE\), com \(AA′\) paralelo a \(TE\). Temos que,

\(\frac{TE}{AA'}=\frac{TB}{AB}\)

Como \(TB=TA+AB,\frac{TE}{AA'}=\frac{TA+AB}{AB}\Leftrightarrow AB\cdot TE=TA\cdot AA'+AB\cdot AA'\)

\(AB=\frac{TA\cdot AA'}{TE-AA'}\)

Assim encontramos a medida procurada \(AB\) uma vez que \(AA′\), \(TE\) e \(TA\) podem ser medidas no local.

Quando se pretendem fazer medições em altura, a dioptra é suspensa verticalmente (FIGURA 2) numa base horizontal sobre um tripé, onde atua como o seu próprio prumo. A linha do diâmetro está na vertical e a alidade na horizontal. A imagem é observada numa vara alta colocada na vertical e segura por um assistente que, na direção do topógrafo, move um cursor para cima ou para baixo de forma a fazer coincidir com a linha horizontal de visão.

Das várias funções associadas à dioptra, o nivelamento é uma das mais importantes, principalmente quando aplicada à construção de canais de irrigação e mais tarde nos aquedutos. Das várias fontes existentes ilustradas com diagramas maioritariamente de representação geométrica e com uso de instrumentos, temos conhecimento de quatro métodos diferentes, propostos por Al-Karaji (dois métodos), Philo de Bizâncio e Heron². Três deles, ainda não muito perfeitos, propostos por Al-Karaji e Philo, e um método proposto por Heron que tornou possível alcançar um grande avanço de tal forma que prevalece até à atualidade. Al-Karaji preocupou-se apenas com o nivelamento para a irrigação e, em ambos os métodos que propõe, tem em conta a altura do instrumento acima do solo. Esta altura, em teoria, deveria ser sempre a mesma, mas devido à irregularidade do terreno e da forma como é fixado ao chão, as leituras podem-se tornar imprecisas.

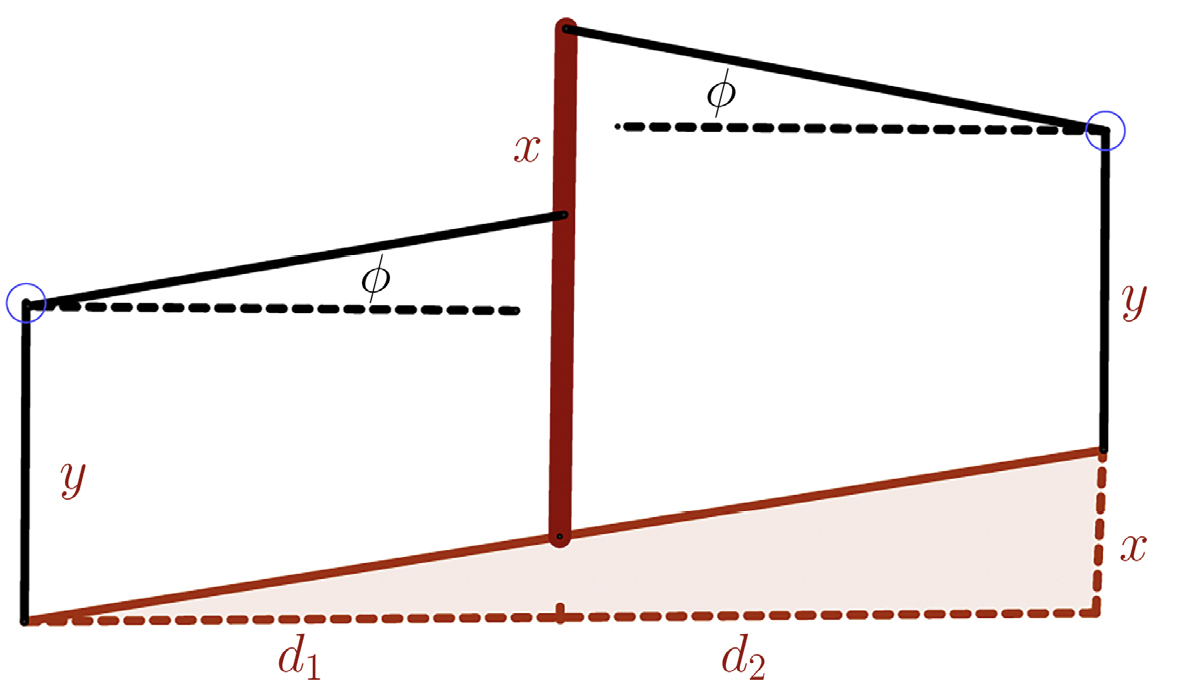
Todo o processo dos diferentes métodos consiste em alternar entre as posições da equipa e a posição e altura do instrumento. Na que se supõe ser a primeira proposta de Al-Karaji (FIGURA 5) pretende-se determinar a altura \(x\) (inclinação do terreno) e, para isso, é fixada uma vara numa posição aleatória. Move-se o instrumento a uma distância \(d_1\) para um dos lados da vara, faz-se a leitura na vara e fixa-se o ângulo de inclinação do instrumento. Sem alterar a configuração do instrumento obtida, move-se o instrumento uma distância \(d_2\), igual a \(d_1\), para o outro lado da vara (FIGURA 5) e faz-se a leitura da nova medida. O valor pretendido \(x\) é obtido fazendo a diferença das duas medidas.

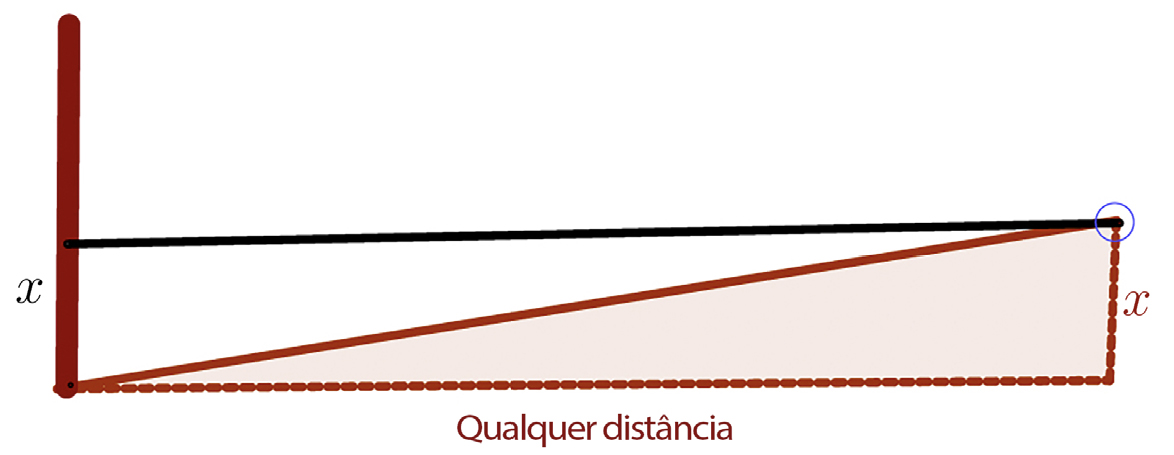
Philo de Bizâncio apresenta um método mais simples e tem por objetivo trabalhar um lote de terra até que esteja nivelado e adequado para irrigação (FIGURA 6). O agrimensor coloca-se ao lado da saída da fonte de água com o instrumento posicionado o mais horizontalmente possível. Do outro lado, e a uma distância qualquer, conveniente, prática e não especificada, está uma equipa com uma vara não graduada, mas pintada com círculos coloridos de forma que sejam visíveis facilmente à distância. Mede-se a altura do chão até à marca e obtém-se a medida \(x\) pretendida.

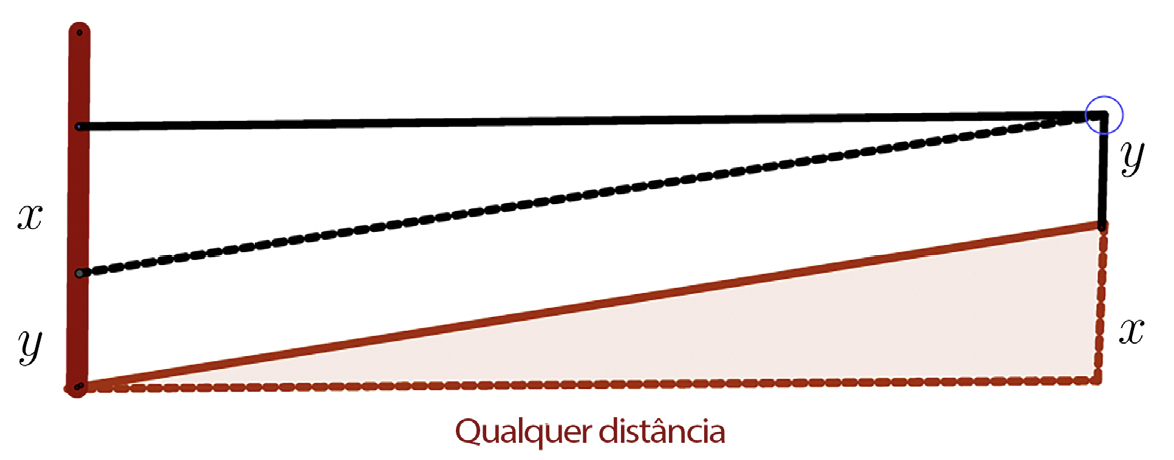
O segundo método de Al-Karaji é semelhante ao método de Philo exceto que tem em conta a altura do instrumento (FIGURA 7). Na vara é marcado a vermelho a altura do instrumento, fazendo a diferença entre a leitura na vara e a altura do instrumento, obtemos a medida \(x\) pretendida. Também aqui, a distância entre o instrumento e a vara não é importante, dando bastante flexibilidade ao agrimensor, não obrigando a fixar distâncias.

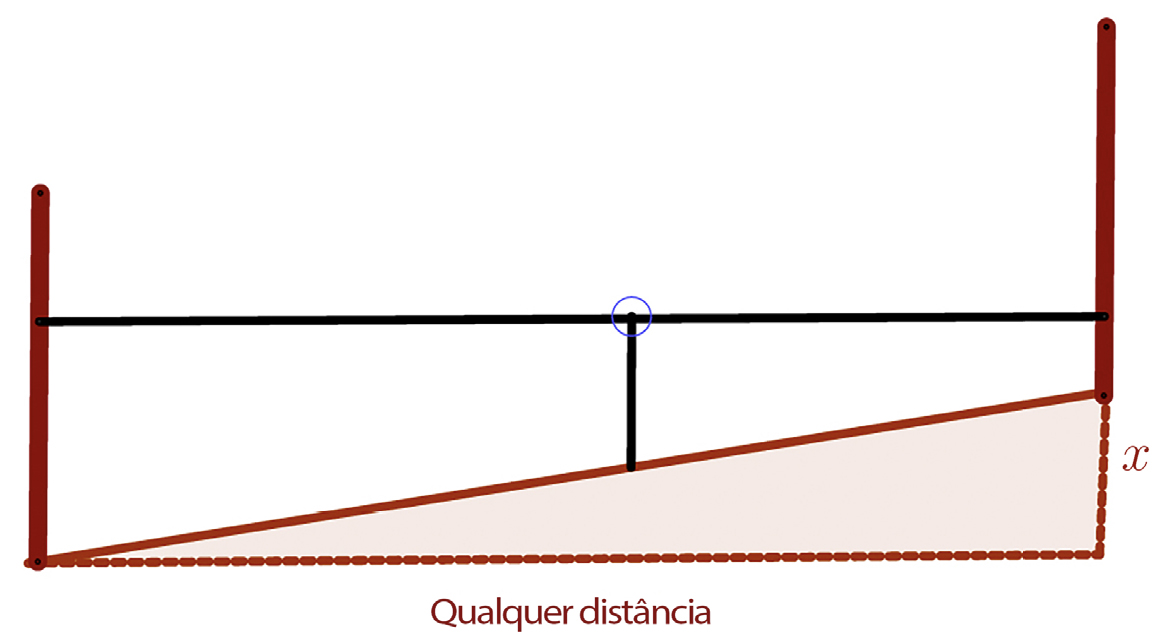
Heron percebeu que, em vez do instrumento mudar de lugar, deveria ser a vara, fixando o instrumento. Desta forma, a altura do instrumento é irrelevante (FIGURA 8). O instrumento é fixado e são colocadas duas varas a uma qualquer distância do instrumento. A altura \(x\) é obtida fazendo a diferença entre as duas leituras nas varas.

Encontrar a altura de um muro sem se aproximar

Outro uso da dioptra, este na esfera militar, consiste em medir a altura de um muro. Um comandante está a cercar uma cidade e quer assaltá-la. Para construir escadas ou torres de cerco precisa saber a altura do muro.

Esta experiência está descrita nos manuais antigos² e requer duas fases para estimar a altura de um muro. Uma fase com a dioptra em modo horizontal (FIGURA 9) e outra com o instrumento em modo vertical (FIGURA 10). Começamos por estimar a distância do muro ao local de observação \(AB\) (FIGURA 9). Posicionamos o observador no ponto \(A\) de forma a que seja possível avistar a base do muro \(B\). Traça-se uma perpendicular \(AF\) a \(AB\) e define-se uma distância arbitrária até um ponto \(G\), situado no segmento \(AF\). Traça-se uma paralela a \(AB\) e, portanto, perpendicular a \(AF\) a partir de \(G\). Colocamos o observador em \(F\) de forma a observar o muro, \(B\), e define-se o ponto \(H\) como sendo o ponto de interseção de \(FB\) com a reta, traçada anteriormente, que é perpendicular a \(AF\) e que passa por \(G\). Após a marcação dos pontos \(A\), \(G\), \(F\), e \(H\) conforme o esquema da FIGURA 9, procede-se à medição de \(AF\), \(GF\) e \(GH\).

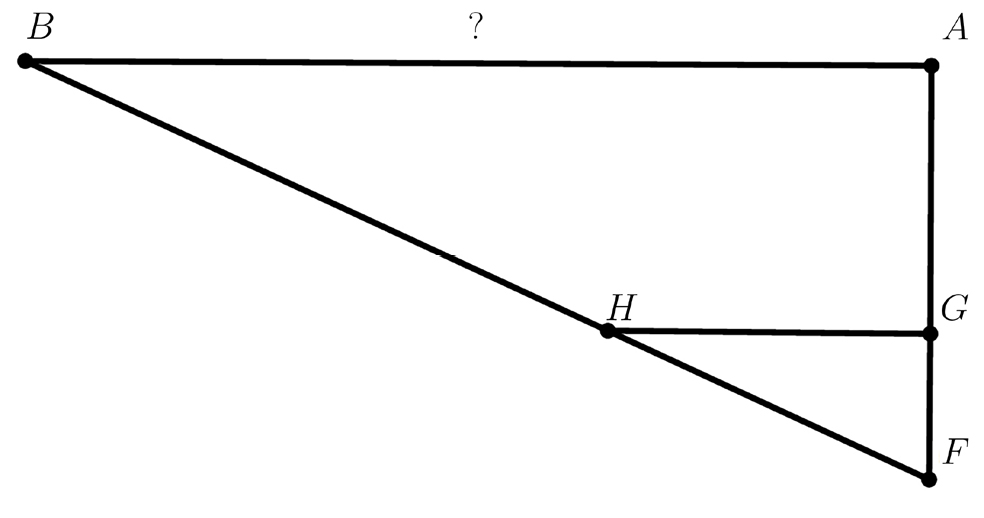
Como os triângulos \(FGH\) e \(FAB\) são semelhantes, podemos estimar o valor de \(AB\):

\(\frac{AB}{GH}=\frac{AF}{GF}\Leftrightarrow AB=\frac{AF\cdot GH}{GF}\) (1)

Para proceder às medições em altura (FIGURA 10), posicionamos o observador em A e uma vara graduada \(ED\) numa posição arbitrária, seja \(E\). Do ponto \(A\) o observador avista o topo do muro, \(AC\), e define o ponto de interseção com a vara em \(D\). Do ponto \(A\), o observador avista a base do muro, \(AB\), e define o ponto de interseção com a vara em \(E\). Desta forma será possível fazer a medição, na vara, de \(ED\), e ainda, a medição da distância \(AE\).

Como estamos novamente perante triângulos semelhantes, \(AED\) e \(ABC\), em conjunto com \(AB\), determinado em (1), conseguimos estimar o valor a altura do muro, \(BC\):

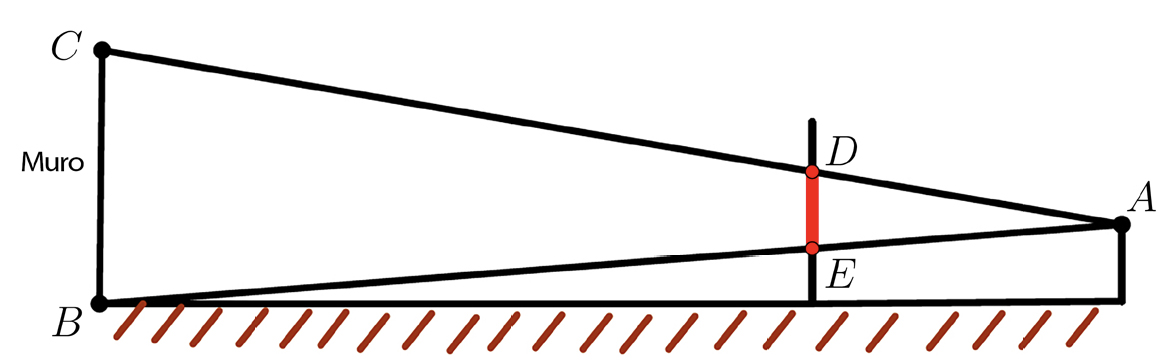
\(\frac{AE}{AB}=\frac{DE}{BC}\Leftrightarrow BC=\frac{DE\cdot AB}{AE}\). (2)

Esta experiência foi realizada por Richard Talbert⁵ para medir a altura de uma chaminé e quando foi feita a medição direta da altura real da chaminé o autor verificou que o cálculo deu um valor menor em 11cm, errando em apenas 0,13%. Dado que a chaminé se encontrava a 293m de distância, foi um resultado respeitável.

Outras possíveis utilizações da dioptra são a determinação da altura perpendicular de um ponto visível acima do plano horizontal desenhado através da nossa posição, sem nos aproximarmos desse ponto e a determinação da profundidade de um fosso perpendicular à altura do seu chão até ao plano horizontal, quer através da nossa posição ou através de qualquer outro ponto.

Encontrar a altura de um ponto visível acima do nosso plano horizontal

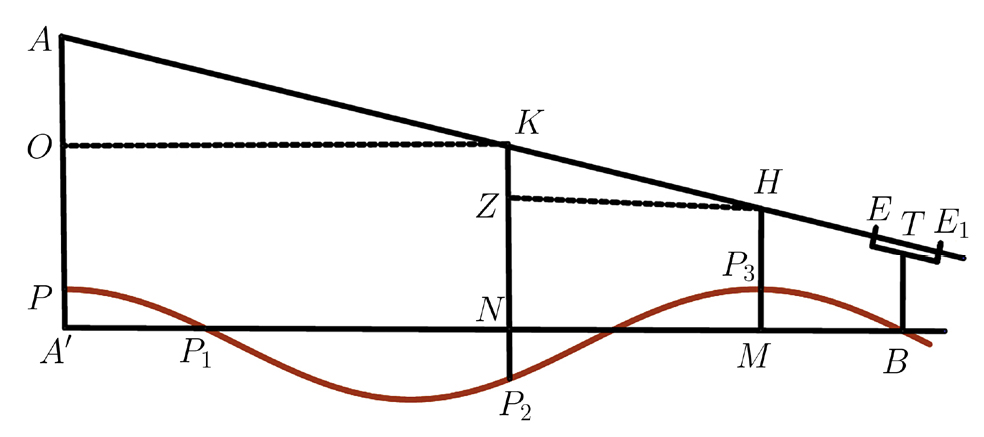
Fixamos o ponto alto \(A\) e posicionamo-nos em \(B^2\). Posicionamos a dioptra em \(B\) (FIGURA 11) apoiada numa coluna, \(BT\). Ajusta-se a alidade \(ETE_1\) de forma a avistar \(A\), fixa-se a sua posição e, sem mover a dioptra, colocamos duas varas verticais \(P_3H\) e \(P_2K\), de alturas diferentes. A mais alta deve ser colocada mais perto do ponto \(A\), \(P_2K\).

Vamos supor que a superfície do solo tem uma forma do tipo \(BP_3P_2P_1\), e imaginamos o plano horizontal a partir da nossa posição como sendo \(BA′\). Movem-se as varas \(P_3H\) e \(P_2K\) até que apareçam em linha reta com o ponto \(A\), sem que a alidade se mova. Observamos o ponto \(H\) na vara \(P_3H\) e o ponto \(K\) em \(P_2K\). A projeção de \(P_3H\) e \(P_2K\) no plano horizontal \(BA′\) define os pontos \(M\) e \(N\) e as linhas \(HZ\) e \(KO\) são paralelas ao plano horizontal \(BA′\). Determinamos o quanto \(P_3\) é maior que \(B\), nivelando \(B\) e \(P_3\) do nosso lado. Depois, determinamos \(P_3M\) e, analogamente, \(NP_2\).

Uma vez que conhecemos o valor de \(HP_3\) e \(HP_2\), determinamos a altura de \(HM\), \(KN\) e obtemos \(KZ\) fazendo a diferença entre as duas alturas. O comprimento \(HZ\) também é conhecido, pois é a distância horizontal entre \(P_3\) e \(P_2\). Portanto, o \(\frac{HZ}{KZ}\) é conhecido.

Consideremos a perpendicular \(AOPA′\) definida a partir de \(A\), com o plano horizontal \(BA′\). Definimos assim dois triângulos semelhantes \(HZK\) e \(KOA\). Então, \(\frac{HZ}{ZK}=\frac{KO}{AO}\) e como \(KO\) é conhecido, pois é igual à distância horizontal entre \(P_2\) e \(P\), obtemos a altura \(AO=KO\times \frac{ZK}{HZ}\).

Sabemos ainda o valor de \(OA′\), uma vez que é igual ao valor de \(KN\). Portanto, a altura \(AA′\) é conhecida:

\(AA'=AO+OA'=AO+KN\)

Encontrar a profundidade de um fosso

Seja \(ABCD\) um fosso e \(B\) um ponto no fundo do fosso². Coloca-se a dioptra num ponto qualquer, seja \(E\) (FIGURA 12). \(EI′\) é o apoio da dioptra e \(I_1I_2\) a alidade. Inclina-se a alidade até que \(B\) seja visível. Imaginamos o solo como sendo \(DEFGM\) e \(ADHO\) o plano base da nossa posição. Alinha-se com a alidade \(I_1I_2\), duas varas \(FN\) e \(MQ\). Avistamos, e é feito o registo dos pontos \(N\) na vara \(FN\) e \(Q\) na vara \(MQ\).

O problema consiste em encontrar a altura da perpendicular de \(B\) ao plano horizontal \(ADO\), seja \(AB\). Considera-se o plano horizontal, \(BO′\), que contém \(B\), prolonga-se a vara \(MQ\) até \(O′\) e a vara \(FN\) até \(H\) e imagina-se ainda, partindo de \(N\), a linha \(NP\) paralela a \(DO\). NP pode ser obtido uma vez que é igual ao intervalo entre F e M, que pode ser medido. Também pode ser medido \(FH\) e \(MO\), e obtemos \(QP\) fazendo a diferença entre \(QPO\) e \(NH\) (procedimento semelhante ao utilizado para encontrar a altura de um ponto visível acima do nosso plano horizontal).

Temos que,

\(\frac{NP}{QP}=\frac{BO'}{QO'}\)

Como \(QO'=QO+OO',OO'=AB\) e \(BO'=AO\), então

\(\frac{NP}{QP}=\frac{AO}{QO+AB}\Leftrightarrow QO.NP+AB.NP=AO.QP\)

Ou seja,

\(AB=\frac{AO.QP-QO.NP}{NP}\).

Conclusão

Apesar de nenhuma dioptra da Antiguidade ter chegado aos nossos dias, sabemos que era o instrumento de levantamento topográfico padrão dos antigos gregos. Conhecemos vários usos da dioptra, que envolvem medir a distância entre pontos afastados sem se aproximar deles, uma prática muito usada para fins militares ou para mapeamento nas montanhas². Este instrumento permitiu o cálculo de distâncias inacessíveis recorrendo ao uso de triângulos semelhantes tendo a vantagem de não necessitar de trigonometria e consequentemente, sem necessidade de recorrer a tabelas trigonométricas. Analisando os vários modelos propostos percebe-se que o método, sendo simples, apenas exige cuidado no manuseamento do instrumento, obtendo um funcionamento tanto mais correto quanto melhor for a precisão da sua construção. As obras de engenharia que sobreviveram mostram a importância do uso da dioptra.