A absorvância (A) corresponde ao simétrico do logaritmo decimal do inverso [ou simétrico do logaritmo] da transmitância (T), que é o quociente entre a potência radiante de saída (após atravessar a amostra em estudo) e a de entrada, respetivamente \(P_\lambda\)^o e \(P_\lambda\). Ou seja, a absorvância é uma medida da “quantidade” de luz que é absorvida pela amostra.

\(T=\frac{P_\lambda}{P_\lambda^o}\)       (1)

\(A=\log\left(\frac{P_\lambda}{P_\lambda^o}\right)=-\log T= \log \left(\frac{1}{T}\right)\)   (2)

e a lei de Lambert-Beer é traduzida pela seguinte expressão matemática:

\(A= εlc\)            (3)

Nesta equação (3), c representa a concentração molar da espécie em solução (mol\(\cdot\)m^-3, no SI), l a distância percorrida pela radiação através da solução (m, no SI) e ε o coeficiente de absorção molar da espécie em estudo (m² mol^-1, no SI).^†

O referido coeficiente é uma medida da capacidade que uma espécie química tem de absorver a radiação, para um determinado comprimento de onda. Na figura 1 é apresentado um esquema do princípio em que se baseia a lei de Lambert–Beer.

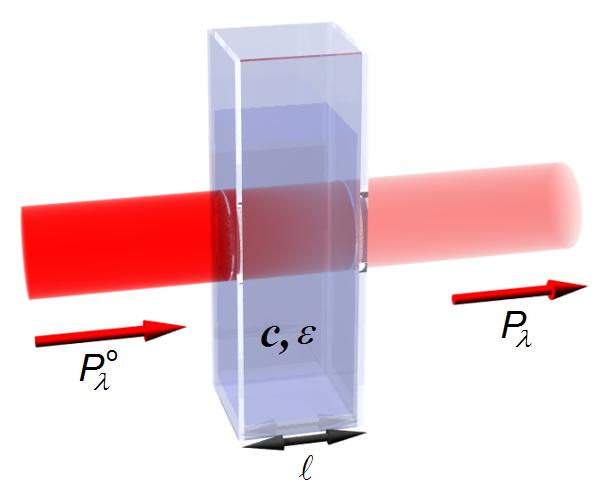
Esta lei foi descoberta pela primeira vez em 1729 pelo matemático, geofísico e astrónomo francês Pierre Bouguer (1698-1758). A sua autoria é, contudo, frequentemente atribuída de forma errada ao matemático, físico e astrónomo francês Johann Lambert (1728-1777). No seu trabalho em 1760¹, Lambert citou a descoberta de Bouguer e constatou que a fração de luz que é absorvida por uma amostra é independente da potência radiante incidente (P \(\lambda\)^o). Este facto é conhecido como lei de Lambert, embora, na realidade, só seja verdadeira se o P \(\lambda\)^o for pequeno e se a extensão de outros fenómenos como a dispersão da luz ou reações fotoquímicas for desprezável. Só 92 anos depois é que a lei foi modificada de forma a incluir a concentração da solução na fórmula de cálculo. Essa modificação foi da autoria do físico e matemático alemão August Beer (1825-1863).

Para a correta utilização e aplicação da lei de Lambert-Beer, é necessário que estejam reunidos alguns pré-requisitos, nomeadamente:

• As partículas (átomos, moléculas ou iões) presentes em solução devem absorver a luz de forma independente entre si;
• O meio absorvente deve ser homogéneo (solução) e não dispersar a radiação;
• A radiação incidente deve estar colimada (raios paralelos entre si) e deve atravessar a mesma distância durante a qual interage com as partículas existentes em solução;
• A radiação deve ser monocromática, isto é, ser composta por apenas um comprimento de onda selecionado (normalmente, correspondente ao comprimento de onda para o qual a absorvância da espécie em estudo é máxima);
• O fluxo da radiação incidente não pode induzir processos que impliquem a desestabilização dos átomos, moléculas ou iões, como por exemplo excitação eletrónica que dê origem a fenómenos de fluorescência ou fosforescência.

Caso não estejam reunidas estas condições, então verificam-se desvios à referida lei. Normalmente, verificam-se desvios à lei para concentrações mais elevadas, pois alguns processos como, por exemplo, a dispersão da luz, são cada vez mais significativos, pelo que não podem ser ignorados.

^†O coeficiente de absorção molar tem m² mol^-1 como unidades SI. No entanto, como a unidade de concentração mais comum é a mol/L (mol dm^-3) e a distância percorrida pela radiação através da solução é mais facilmente medida em cm, resulta que a unidade mais comum de ε é mol^-1 L cm^-1 (= 0,1 m² mol^-1).