A lei da gravitação universal foi enunciada por Isaac Newton (1643-1727) em 1687 na sua obra Philosophiæ Naturalis Principia Mathematica. Esta lei explicita a forma da força atrativa que existe entre dois corpos devido ao facto de terem massa, mas nada diz sobre a sua origem, que só foi explicada mais tarde pela Teoria da Relatividade Geral de Albert Einstein. Nesta obra Newton também mostrou como as Leis de Kepler são consequência desta lei.

A força gravitacional entre dois corpos pontuais, com massas m₁ e m₂, é diretamente proporcional ao produto das massas gravitacionais, e inversamente proporcional ao quadrado da distância entre eles. A força tem a direção da reta que une as massas pontuais.

Matematicamente, a força que o corpo de massa m₁ exerce sobre o corpo de massa m₂ é dada por:

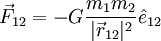
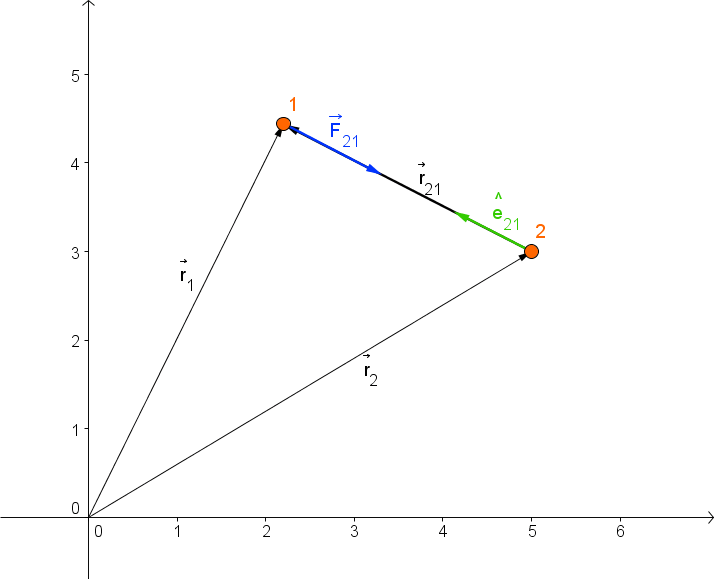
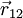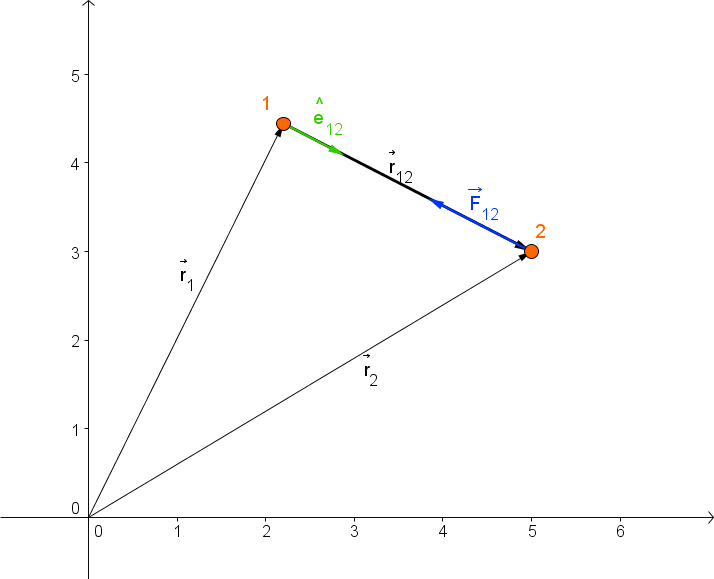
em que é o vetor com origem no corpo m₁ e extremidade no corpo m₂, e 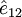é um vetor unitário com a direção e sentido de 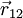, como ilustrado na figura 1.

G é a constante de gravitação universal, que no Sistema Internacional tem o valor 6.674 28 (67) E-11 m³kg^-1s². ¹

A força gravitacional satisfaz a lei do par ação-reação de Newton. Assim, a força que o corpo m₂ exerce sobre o corpo m₁, \(\vec{F}_{21}\) é simétrica à força \(\vec{F}_{12}\) e aplicada no corpo m₂:

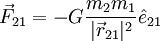
como indicado na figura 2. Note-se qu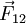e e 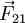, formando um par ação-reação, estão aplicadas em corpos distintos.

Apesar de ser válida para a maioria dos sistemas gravitacionais observados, há fenómenos que só são explicados utilizando Relatividade Geral. É o caso da precessão da órbita de Mercúrio e da deflexão de raios de luz por efeitos gravitacionais. A Relatividade Geral é mais utilizada quando é requerida uma extrema precisão nos resultados, ou quando os sistemas envolvem corpos muito massivos ou muito densos.