Notas

Raio da circunferência é um segmento de reta cujos extremos são o centro e qualquer ponto da circunferência. Note-se, todavia, que também se pode chamar "raio" ao comprimento deste segmento. Observe-se ainda que uma circunferência de raio 0 é, na verdade, uma circunferência degenerada.


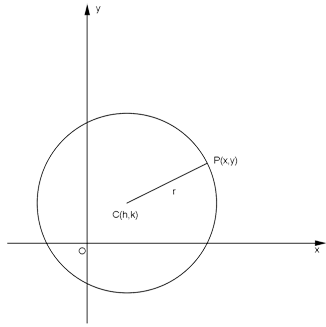
Figura 1. Circunferência de centro C e raio r.

Na figura, o centro é o ponto C e o raio é o segmento [CP] (ou o seu comprimento).

Uma circunferência determina num plano três regiões:


  • Uma curva: a própria circunferência;
  • Uma região que contém o centro e os pontos interiores dos raios, chamada interior ou disco (da circunferência);
  • Uma região que contém os pontos existentes nos prolongamentos dos raios, chamados pontos exteriores.

Arco de circunferência é qualquer porção, da circunferência, compreendida entre dois dos seus pontos.

Aos pontos que definem um arco de circunferência chamamos extremidades do arco.

Uma circunferência - enquanto lugar geométrico dos pontos P de coordenadas (x,y) cuja distância ao centro C, de coordenadas (h,k), é igual a r (número real não negativo) - representa-se analiticamente por:

(x−h)2+(y−k)2=r2


Exemplos


  1. A equação (x−2)2+(y+1)2=9 define, analiticamente, a circunferência de centro no ponto de coordenadas (2,−1) e raio 3.
  2. A equação x2−2x+y2−5=0 define, analiticamente, a circunferência de centro no ponto de coordenadas (1,0) e raio 2.

Note-se que x2−2x+y2−5=0 equivale a (x−1)2+y2=4.