Triângulo no plano

Um triângulo é um polígono com três lados. É pois a região do plano limitada por três segmentos de reta \(a\),\(b\) e \(c\) (os seus lados), contíguos dois a dois nas suas extremidades \(A\),\(B\) e \(C\) (os vértices).

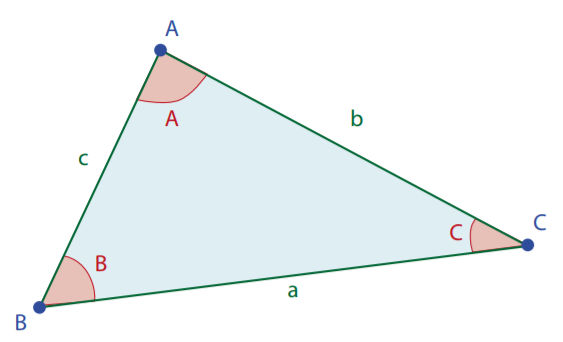
Um triângulo \(ABC\) possui seis elementos principais (ver FIGURA 1)

• lados \(a\),\(b\) e \(c\)
• 3 vértices \(A\),\(B\) e \(C\)

\(a\) diz-se o lado oposto ao vértice \(A\), \(b\) o lado oposto ao vértice \(B\) e \(c\) o lado oposto ao vértice \(C\). Os ângulos internos, ou as suas medidas, são designadas habitualmente pelas letras maiúsculas \(A\),\(B\),\(C\), afetas aos respetivos vértices (FIGURA 1).

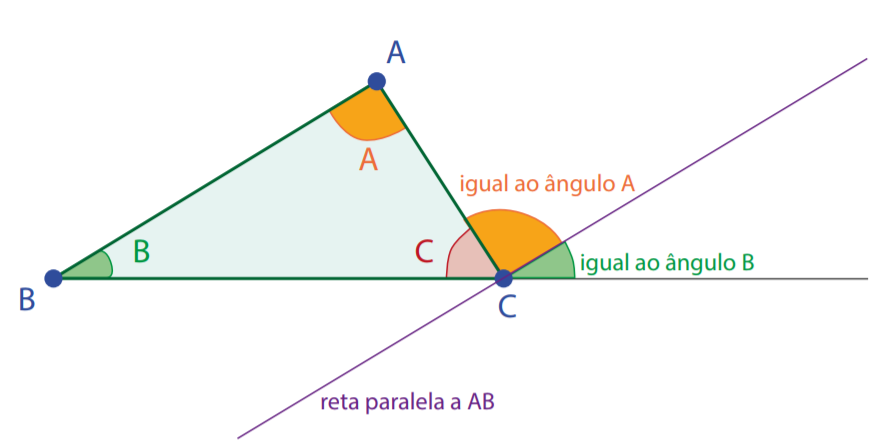
Um dos resultados básicos é o seguinte "A soma dos ângulos internos de um triângulo plano é igual a 180º". A demostração pode ser vista na FIGURA seguinte:

Classificação de triângulos

Os triângulos podem ser classificados quanto aos seus lados e quanto aos seus ângulos.

Quanto aos seus lados os triângulos classificam-se em:

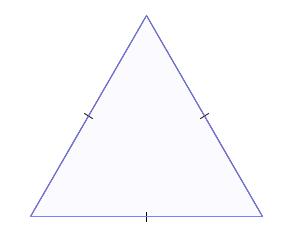	Triângulo equilátero: tem os seus três lados com o mesmo comprimento;
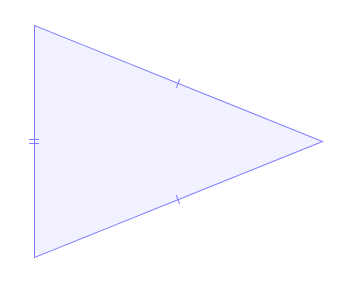	Triângulo isósceles: tem dois lados com o mesmo comprimento;
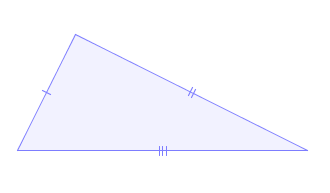	Triângulo escaleno: tem todos os lados com comprimento desigual.

Quanto os seus ângulos os triângulos classificam-se em:

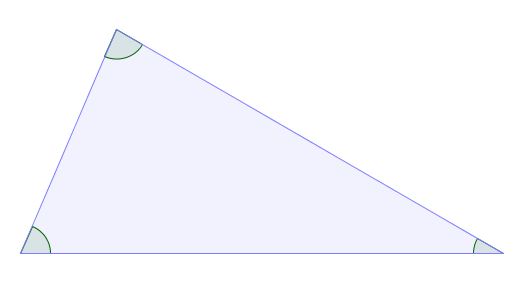	Triângulo acutângulo: tem os três ângulos internos agudos;
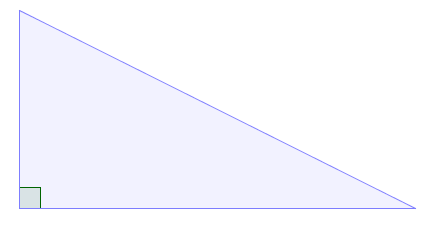	Triângulo retângulo: um dos três ângulos do triângulo é um ângulo reto;
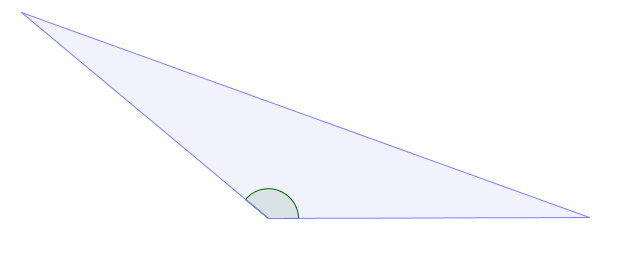	Triângulo obtusângulo: um dos três ângulos do triângulo é um ângulo obtuso.

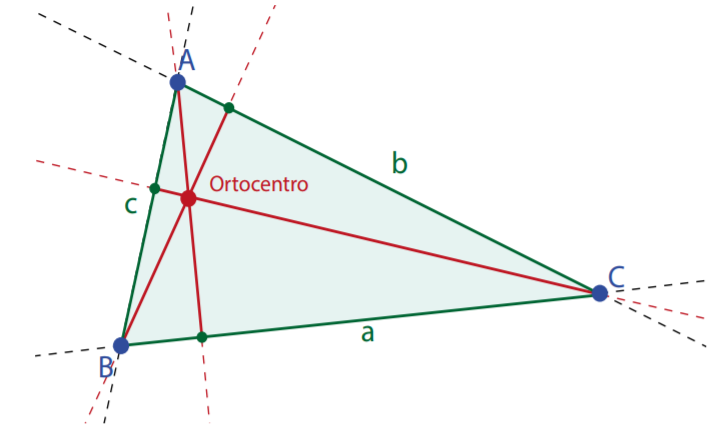
Um triângulo ABC possui vários elementos secundários (ver FIGURA 4)

• 3 alturas. Uma altura é a reta perpendicular baixada de um vértice para o lado oposto.
• Facto notável: as 3 alturas intersetam-se num único ponto a que se chama o ortocentro do triângulo.
• Por altura também se entende o comprimento do segmento de reta baixado de um vértice para o lado oposto (FIGURA 4). Este conceito é útil quando se discutem questões métricas num triângulo. O contexto tornará claro a que nos referimos.
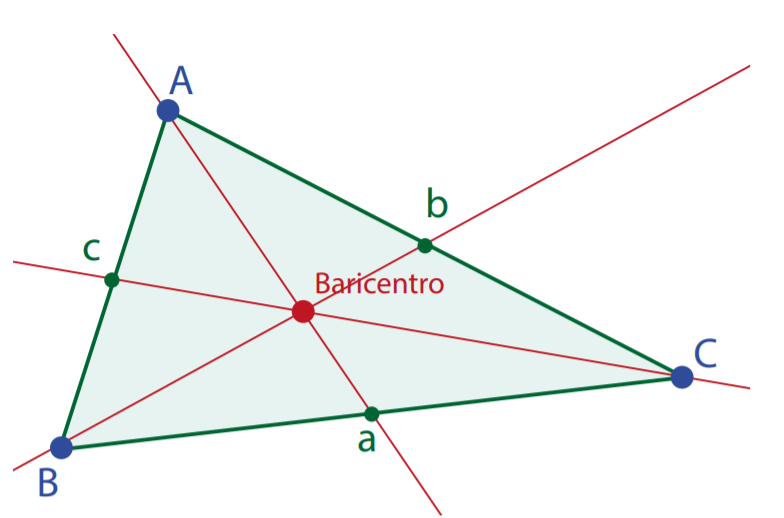
• 3 medianas. Uma mediana é a reta que une um vértice ao ponto médio do lado oposto.
• Facto notável: as 3 medianas intersetam-se num único ponto a que se chama o baricentro ou centro de gravidade do triângulo.

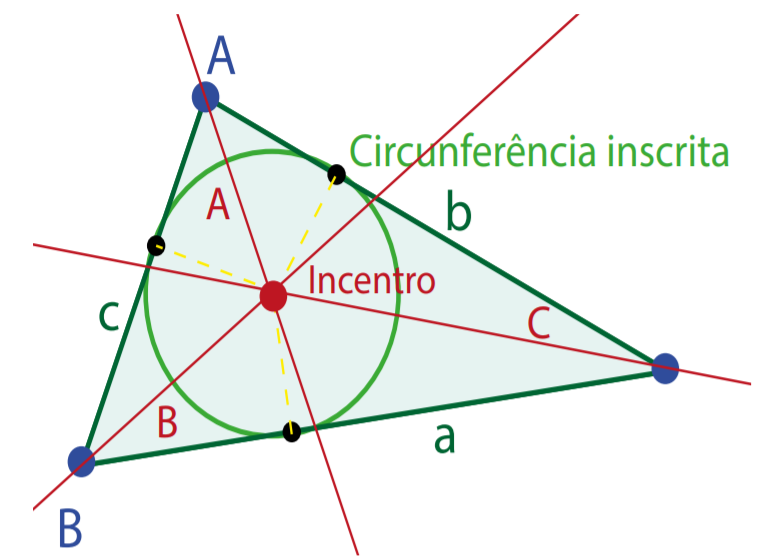
• 3 bissetrizes - as bissetrizes dos seus ângulos internos.
• Facto notável: as 3 bissetrizes intersetam-se num único ponto a que se chama o incentro do triângulo. O incentro é o centro da circunferência inscrita no triângulo (tangente a cada um dos lados).

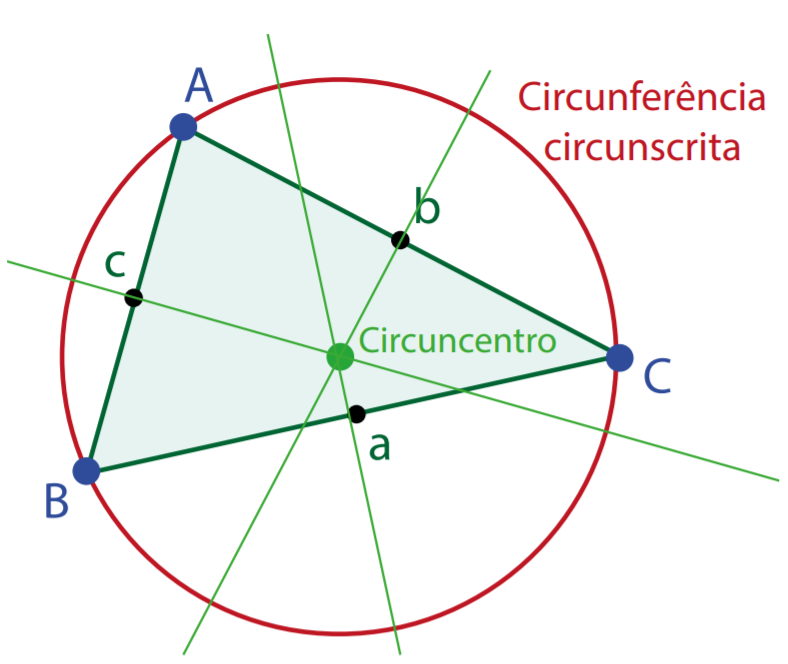
• 3 mediatrizes - as mediatrizes dos seus lados, isto é, as retas perpendiculares a cada um desses lados e que passam pelos respetivos pontos médios.
• Facto notável: as 3 mediatrizes intersetam-se num único ponto a que se chama o circuncentro do triângulo. O circuncentro é o centro da circunferência circunscrita no triângulo (que passa pelos 3 vértices).

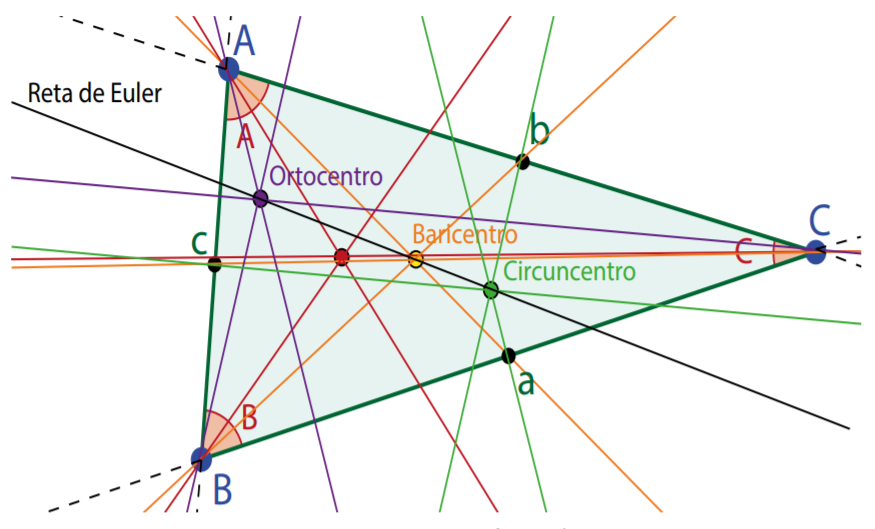
A reta de Euler. Um facto extraordinário.

O ortocento, baricentro e circuncentro de um triângulo, que se definiram anteriormente, passam todos por uma mesma reta a que se chama a reta de Euler (FIGURA 7). Em geral o incentro não pertence à reta de Euler!

Teorema de Pitágoras

Num triângulo retângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos:

\[a^2=b^2+c^2\]

Existem dezenas de demonstrações do Teorema de Pitágoras. Em 1940, num livro de Elisa Loomis, intitulado The Pythagorean Proposition, incluem-se 367 provas diferentes!

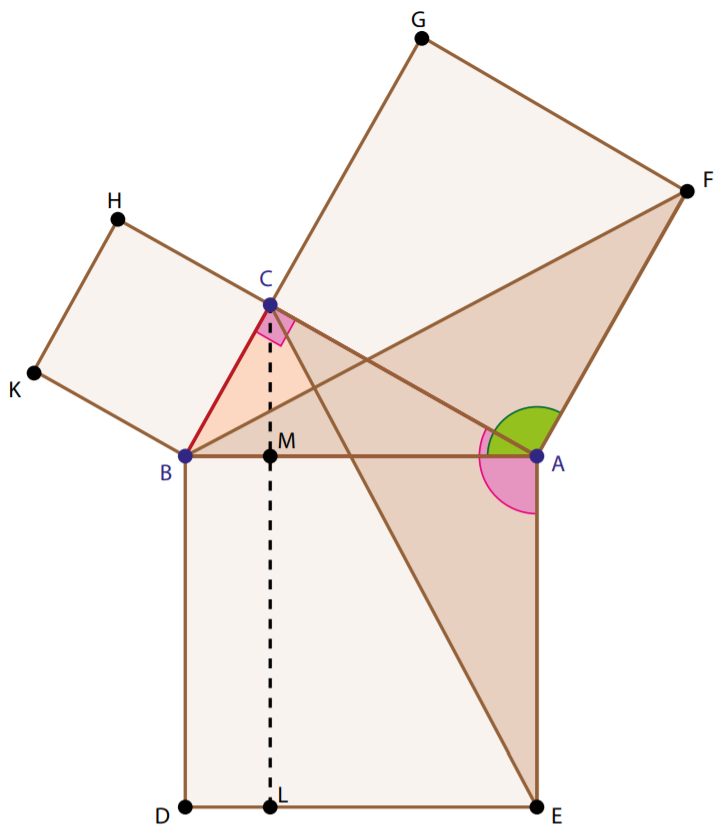
Na figura ilustra-se a demonstração de Euclides:

1. Os triângulos \(ABF\) e \(AEC\) são "iguais" (isto é, são isométricos). De facto, \(AE=AB\), \(AF=AC\) e \(\angle(BAF)=\angle(CAE)\).
2. Para calcular a área do triângulo \(ABF\), retângulo em \(C\), Euclides faz intervir a base \(AF\) e a altura.

Outros triângulos

Como vimos, um dos resultados básicos para triângulos no plano (Euclideano) é o seguinte "A soma dos ângulos internos de um triângulo plano é igual a 180º".

É possível imaginar outras geometrias onde este resultado é falso.

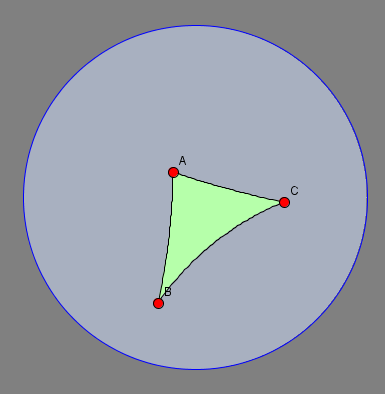
Por exemplo, imaginemos uma geometria na superfície de uma esfera onde as Retas são os círculos máximos,isto é, as circunferências obtidas intersetando a esfera com um plano que passa no seu centro.

Nesta geometria esférica, a soma dos ângulos internos de um triângulo esférico é superior a 180º!

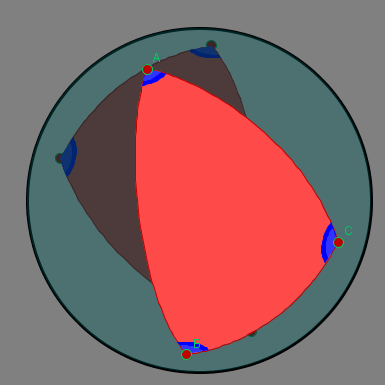
Um outro exemplo, imaginemos uma geometria no interior de um disco plano \(D\), mas em que as Retas são as partes em \(D\) das circunferências, ou das retas usuais, ortogonais à circunferência do bordo de \(D\).

Nesta geometria, dita hiperbólica, a soma dos ângulos internos de um triângulo esférico é inferior a 180º!