Filtro de Velocidades
📧
- Faculdade de Ciências da Universidade do Porto
Referência Ferreira, M., (2013) Filtro de Velocidades, Rev. Ciência Elem., V1(1):037
DOI http://doi.org/10.24927/rce2013.037
Palavras-chave Filtro; Velocidades; eléctrico; magnético; uniformes;
Resumo
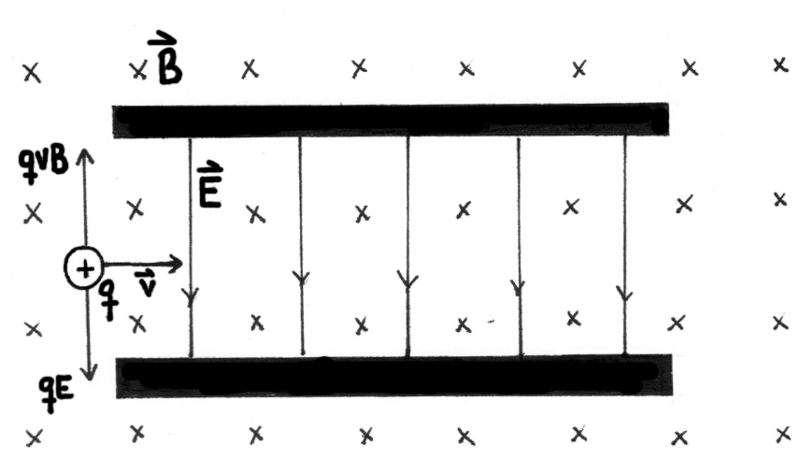
Suponhamos que numa região do espaço existe um campo elétrico e magnético, ambos uniformes, de maneira que o campo magnético aponta no sentido negativo do eixo dos \(zz\) e o campo elétrico aponta no sentido negativo do eixo dos \(yy\). No que se segue, desprezamos os efeitos de bordo nos campos e a interação gravitacional.
Uma partícula com carga \(q\), velocidade de módulo v e direção segundo o eixo dos \(xx\), e massa \(m\) ,ao entrar na região onde estão definidos os dois campos, fica sujeita ao efeito de duas forças: uma devido à sua interação com o campo elétrico, outra devido à sua interação com o campo magnético. Estas forças são dadas pelas seguintes expressões:
\(\overrightarrow{F}_e= -qE\widehat{y}\)
\(\overrightarrow{F}_m= q\overrightarrow{v}\times\overrightarrow{B}=-qvB(\widehat{x}\times\widehat{z})=qvB\overrightarrow{y}\).
De um modo geral, em que a partícula tem uma velocidade arbitrária, esta será desviada em relação à direção paralela ao eixo dos \(xx\), devido à resultante das forças que nela atua não ser nula. Contudo, existe um caso em que a trajetória da partícula coincide com a direção \(xx\). Note-se que a força magnética depende da velocidade da partícula, enquanto que a força elétrica é independente da velocidade. Para uma dada velocidade (grandeza vetorial), as forças que atuam na partícula têm resultante nula e, pela Lei da Inércia, a velocidade da partícula é constante e esta descreve uma trajetória retilínea na região onde existem os campos. Neste caso, e recordando que a velocidade da partícula é perpendicular ao campo magnético, as forças elétrica e magnética têm a mesma direção, mas sentidos opostos. Para que a resultante seja nula, é necessário garantir que:
\(qvB= qE\Leftrightarrow v=\frac{E} {B}\).
No caso em que a velocidade da partícula não tiver a direção do eixo \(xx\), as forças elétrica e magnética nunca têm resultante nula. A força resultante tem uma componente que é perpendicular à velocidade e, por isso, a velocidade também muda de direção \(xx\). Neste caso, a trajetória da partícula é uma curva, afastando-se da direção xx. Note-se que este dispositivo consegue retirar partículas de um feixe, com velocidades distintas, deixando passar apenas as que têm a velocidade adequada - filtro de velocidades. O valor da velocidade é dado pela equação anterior. Este dispositivo é utilizado, por exemplo, num espectrómetro de massa.
Este artigo já foi visualizado 8426 vezes.



