Cone de revolução é o sólido geométrico gerado por um triângulo retângulo que roda em torno de um dos seus catetos até completar uma volta completa.

Nota Cone de revolução é também designado por cone reto circular e corresponde à porção de espaço delimitado por uma hemisuperfície cónica de revolução e um plano perpendicular ao eixo.


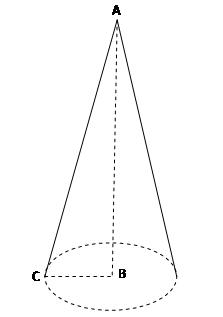
Figura 1. Cone de revolução
Figura 1. Cone de revolução gerado por \( [ABC]\) no eixo \([AB]\).

O triângulo retângulo, na definição, diz-se triângulo gerador do cone. Na figura, o triângulo gerador do cone é \([ABC]\).

A hipotenusa do triângulo gerador, na figura \([AC]\), chama-se a geratriz do cone e o cateto \([AB]\) é o eixo de rotação. O cateto \([BC]\) (perpendicular ao eixo) é um raio do círculo gerado na rotação. Este círculo diz-se a base do cone.

A altura de um cone de revolução é dada pela medida do seu eixo.