Área de um paralelogramo

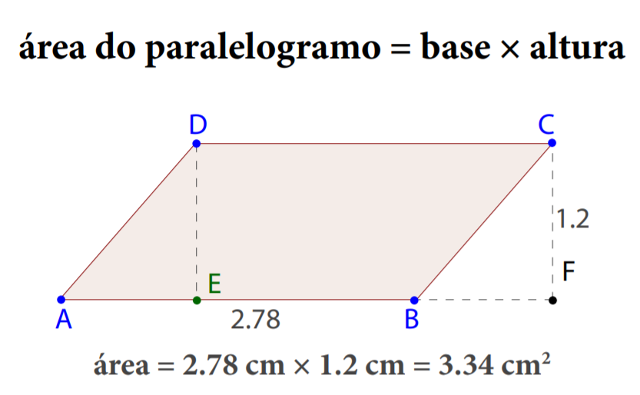
A área de um paralelogramo é igual ao produto (dos comprimentos) da sua base pela sua altura

$\mbox{área do paralelogramo}=\mbox{base}\times \mbox{altura}$

De facto, os triângulos retângulos $AED$ e $BFC$ são iguais, por terem as hipotenusas iguais $\left(AD=BC\right)$ e um cateto igual $\left(DE=CF\right)$. Retirando o triângulo $AED$ ao paralelogramo $ABCD$ e substituindo-o pelo triângulo $BFC$, obtemos um retângulo com a mesma área do paralelogramo. A área deste é, pois, dada pela fórmula anterior.

Área de um triângulo

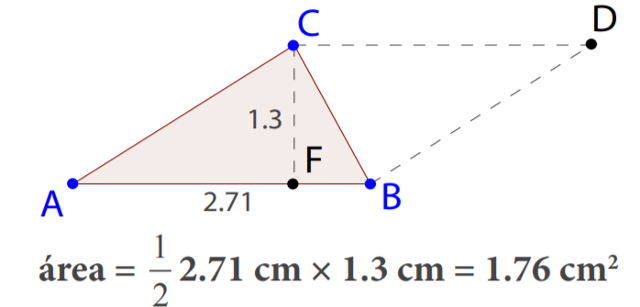
A área de um triângulo é igual a metade do produto (dos comprimentos) da sua base pela sua altura

$\mbox{área do triângulo}=\displaystyle\frac{1}{2}\mbox{base}\times \mbox{altura}$

De facto, como se indica na imagem a cima, dado o triângulo $ABC$, podemos construir um paralelogramo $ABDC$, cuja área é igual ao produto da sua base pela sua altura, como vimos no ponto anterior. Mas a área do paralelogramo $ABDC$ é o dobro da área do triângulo $ABC$, uma vez que os triângulos $ABC$ e $BCD$ são congruentes.

Área de um trapézio

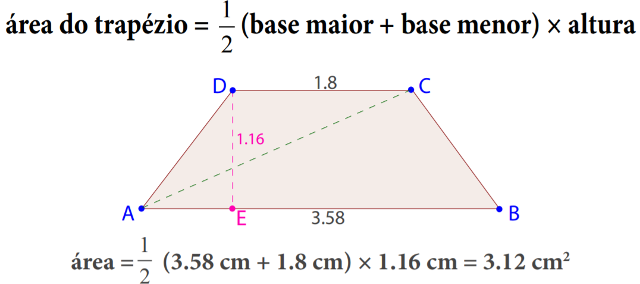
A área de um trapézio é igual a metade do produto (dos comprimentos) da soma das suas bases pela sua altura

$\mbox{área do trapézio}=\displaystyle \frac{1}{2}\left(\mbox{base maior}+ \mbox{base menor}\right)\times\mbox{altura}$

De facto, consideremos, por exemplo, a diagonal $AC$ do trapézio $ABCD$. Esta diagonal divide o trapézio em dois triângulos - o triângulo $ADC$, cuja área é igual a metade do produto da base maior $AB$, do trapézio, pela sua altura, e o triângulo $DCA$, cuja área é igual a metade do produto da base menor $DC$, do trapézio, pela sua altura. Basta agora somar as áreas destes dois triângulos para obter a área do trapézio.

Área de um polígono regular

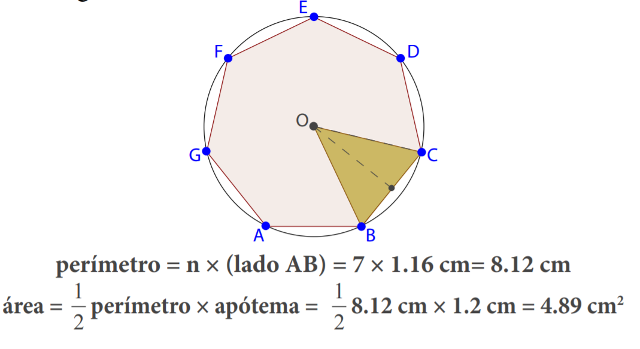
A área de um polígono regular é igual a metade do produto do seu perímetro pela seu apótema

$\mbox{área do polígono regular}=\displaystyle\frac{1}{2}\mbox{perímetro}\times \mbox{apótema}$

Seja $n$ o número de lados do polígono regular dado. Podemos dividir esse polígono em $n$ triângulos iguais cuja base é igual ao lado do polígono e cuja altura é igual ao apótema do polígono (na imagem, consideramos um polígono com um número de lados que pode variar de $n=3$ a $n=10$ e um dos $n$ triângulos da subdivisão referida - o triângulo $OBC$). Basta agora somar as áreas desses $n$ triângulos.

Área de um polígono qualquer

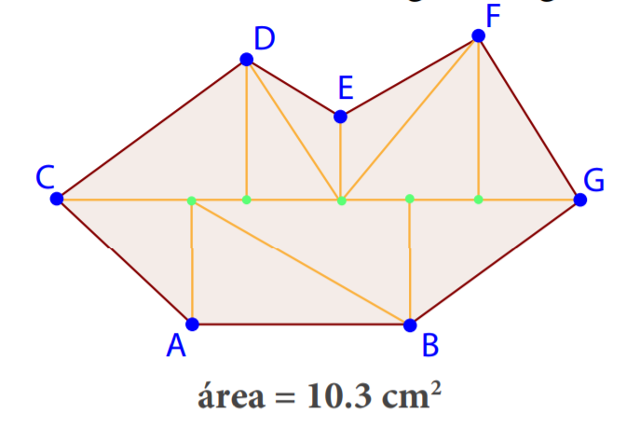
Neste caso não há uma fórmula para calcular a área. Uma forma de a calcular é decompor o polígono em triângulos, como se ilustra na imagem a cima.

Calculamos então a área de cada triângulo e somamos todas essas áreas para obter a área do polígono.

Materiais relacionados disponíveis na Casa das Ciências:

1. Calçada Portuguesa, de Fernanda Martins F. Santos;
2. Jardim dos sete castelos, de Aurélia Freire;
3. Áreas e perímetros numa quinta geométrica, de Sílvia Costa e Sílvia Couto;
4. Áreas e perímetros, de Casa das Ciências.