Considerem-se as correspondências abaixo definidas:

  • Correspondência i

    • Figura 1. Correspondência i de {1,2,3,4,5} em {1,2,3,4,5}

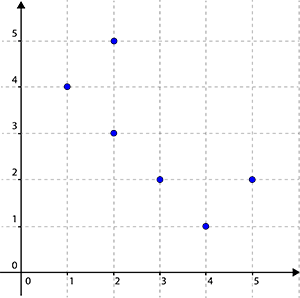
    A correspondência i não é uma função porque o elemento "2", do conjunto de partida, admite dois representantes diferentes, "3" e "5", no conjunto de chegada.


  • Correspondência j

    • Figura 2. Correspondência j de {1,2,3,4,5} em {1,2,3,4,5}

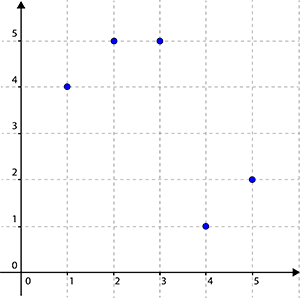
    A correspondência j é uma função porque cada elemento no conjunto de partida admite um e um só representante no conjunto de chegada.

    Todavia, j não é injetiva porque "2" e "3" são dois objetos distintos com a mesma imagem "5".

    j também não é sobrejetiva porque "3" é um elemento do conjunto de chegada que não representa nenhum objeto.


  • Correspondência l

    • Figura 3. Correspondência l de {1,2,3,4,5} em {1,2,3,4,5}

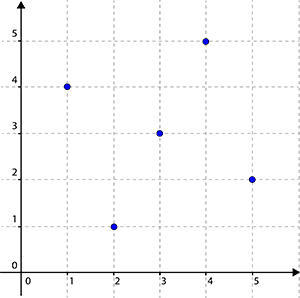
    A correspondência l é uma bijeção.

    É uma função (a cada elemento do conjunto de partida corresponde um e um só elemento no conjunto de chegada), é injetiva (objetos distintos têm imagens distintas) e é sobrejetiva (todos os elementos do conjunto de chegada representam algum objeto).


Materiais relacionados disponíveis na Casa das Ciências:


  1. Estudo de função, de José Leal;
  2. Gráficos de funções racionais, de João Vieira Gomes.