Os diagramas de Venn são representados por linhas fechadas, desenhadas sobre um plano, de forma a representar os conjuntos e as diferentes relações existentes entre conjuntos e elementos.

Exemplo:

Considerando o conjunto dos números naturais N={1,2,3,4,⋯}, sejam U o conjunto dos números naturais até 25 e A e B, respetivamente, os conjuntos dos números primos até 25 e números pares até 25:

A={2,3,5,7,11,13,17,19,23},B={2,4,6,8,10,12,14,16,18,20,22,24}

Recorrendo à utilização de Diagramas de Venn podemos visualizar os conjuntos anteriores, assim como as seguintes operações:

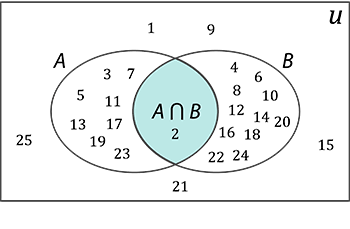
  • Interseção entre A e B

    • A∩B={2}



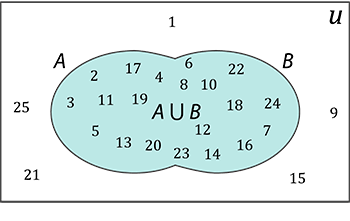
  • Reunião entre A e B

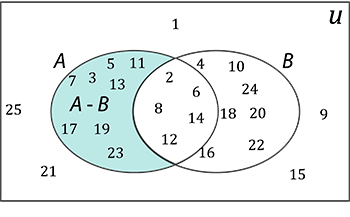
    • A∪B={2,3,4,5,6,7,8,10,11,12,13,14,16,17,18,19,20,22,23,24}



  • Diferença entre A e B ou complementar relativo de A em B (A\B ou A-B)

    • A−B={3,5,7,11,13,17,19,23}



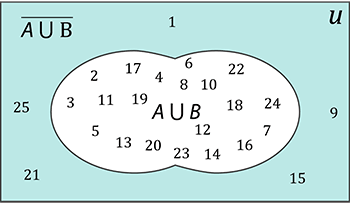
  • Complementar da reunião entre A e B

    • ¯A∪B:=U−(A∪B)={1,9,15,21,25}



Observação:

Dado um conjunto M o seu conjunto complementar pode ser designado simbolicamente por ˉM, MC e CM.

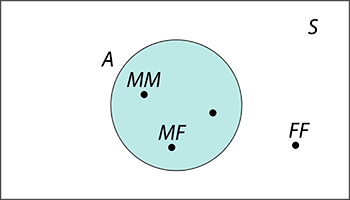
Em Estatística utilizam-se diagramas de Venn para visualizar o espaço de resultados e os acontecimentos associados a um fenómeno aleatório. Para representar o espaço de resultados S utiliza-se um retângulo e no seu interior regiões fechadas para representar os acontecimentos A, B,...

Consideremos, por exemplo, a experiência aleatória que consiste em verificar o sexo dos filhos das famílias com 2 filhos. O espaço de resultados é constituído pelos resultados S ={MM,MF,FM,FF}. Seja A o acontecimento “Pelo menos um dos filhos é do sexo masculino”. Representando num diagrama de Venn, temos




Notas históricas

Os diagramas de Venn foram desenvolvidos pelo matemático britânico John Venn.


Materiais relacionados disponíveis na Casa das Ciências:

  1. Números reais, de Cláudia Maria Diegues Araújo;
  2. Conjuntos, de Casa das Ciências.