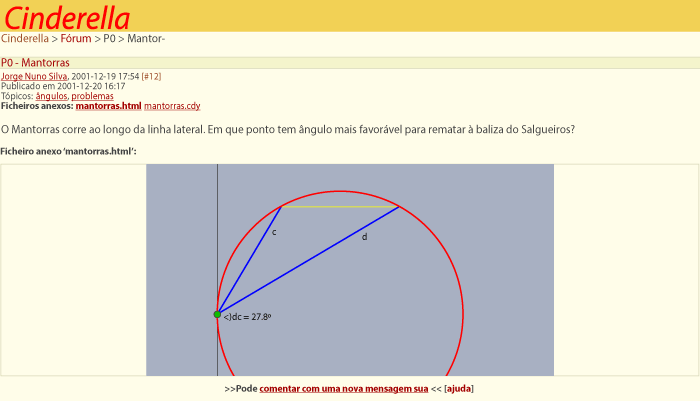
Entre nós foi criado um forum (http://cinderella.ptmat.fc.ul.pt/) onde as construções geométricas se podiam partilhar e comentar. Este site serviu também como apoio a algumas disciplinas universitárias, nomeadamente nas universidades de Lisboa e Coimbra. Muito do material aí disponibilizado, em forma de costruções interativas, exportadas em Java para o ambiente web é ainda muito relevante. Uma das primeiras contribuições permite experimentar uma corrida do Mantorras ao longo da linha lateral, procurando o ângulo/momento ótimo para rematar (os jogadores passam, a geometria fica!...).

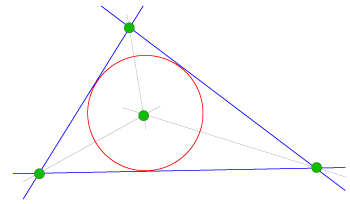
Em boa hora o governo português distribuiu por todas as escolas do país a versão portuguesa do Cinderella, que tivemos o prazer de traduzir. Este programa está particularmente vocacionado para as atividades letivas, por ser simples de implementar e partilhar, e também por proporcionar instrumentos originais, como o detetor de teoremas, que assinala qualquer facto geométrico relevante na construção (como a colinearidade de três pontos construídos independentemente, ou a concorrência num ponto de mais de duas retas, etc) e a possibilidade de gerar exercícios interativos, que reconhecem a bondade das respostas independentemente dos métodos seguidos (desde que válidos, naturalmente).

A exploração da Geometria Euclidiana é particularmente adequada a este software, onde os cliques correspondem exatamente à utilização pura da régua e compasso de Euclides.

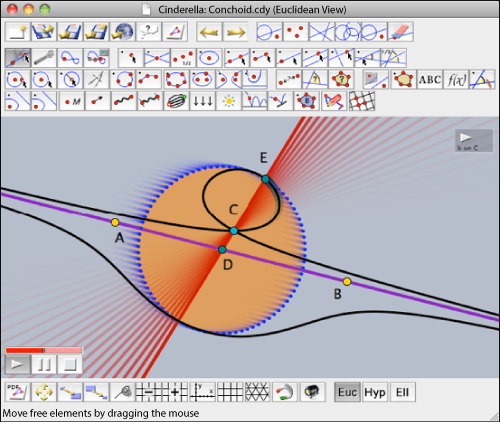
As animações e suas exportações para a web são particularmente interessantes, pela simplicidade de construção e robustez de comportamento. Como os autores explicam no Manual, essa robustez deve-se ao facto de todo o programa estar construído sobre um núcleo matemático interno muito sofisticado.

Ao longo do tempo outros programas têm surgido, alguns disponibilizados gratuitamente na internet. Talvez essa tenha sido uma das razões que levaram os autores a criar uma nova versão, também ela de distribuição livre.

O Cinderella.2 apresenta, contudo, inovações espetaculares. Tentaremos referir algumas.
São introduzidas as transformações do plano, com aplicações naturais ao estudo de frisos, padrões, fractais, etc. A simplicidade de interação mantém-se, privilegiando-se a utilização do rato.

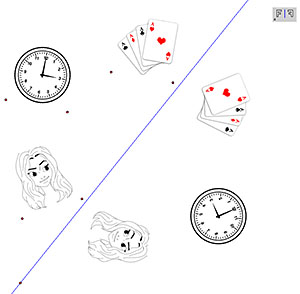
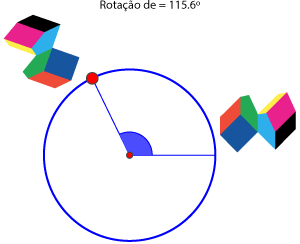
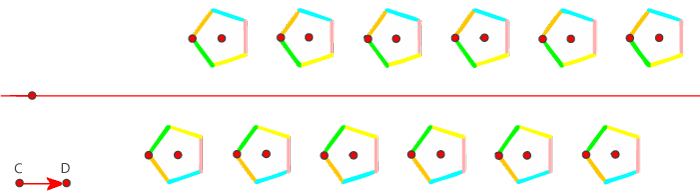
Muitas outras transformações são implementáveis com poucos cliques do rato.
Agora é também fácil tratar gráficos de funções em geral, quer para o seu estudo, quer para produção de ficheiros gráficos de grande qualidade.

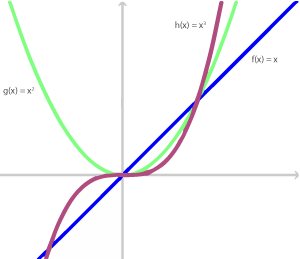
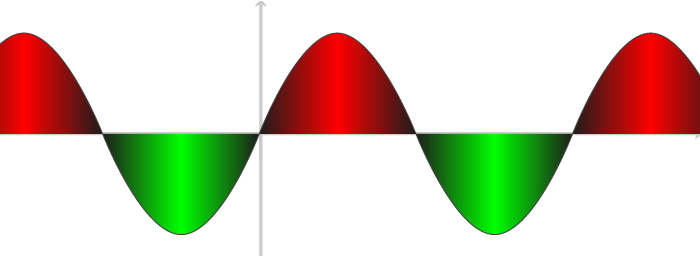
O Cinderella continua a proporcionar ferramentas especializadas noutras geometrias (hiperbólica, elíptica). A nova versão inclui também a implementação de vários elementos próprios à simulação física, o CindyLab. Emular órbitas de planetas, gravidade, conservação de momento, etc são construções ao alcance do utilizador médio.

Por fim, é possível operar com o Cinderella por intermédio da sua linguagem de programação própria – o CindyScript – disponibilizada a todos pelos autores.

Tentámos dar uma pálida ideia das potencialidades deste software maravilhoso. Sugerimos ao leitor a consulta do seu Manual, publicado pela Springer (The Cinderella.2 Manual: Working with The Interactive Geometry Software), bem como a página http://cinderella.de.

Jorge Nuno Silva
Centro Interuniversitário de História das
Ciências e da Tecnologia (CIUHCT)
Associação Ludus