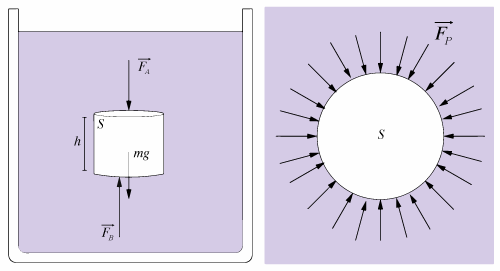
Figura 1. À esquerda: um corpo cilídrico, de secção reta constante, encontra-se totalmente imerso num líquido; por simplicidade, admite-se que as bases do cilindro são horizontais. As setas verticais representam as forças de pressão que atuam na direção vertical; note-se que a força de pressão que atua na base inferior tem módulo superior á que atua na base superior. À direita: corte transversal do cilindro por um plano horizontal. As setas representam as forças de pressão que atuam na superfície lateral do cilindro. Em todos os pontos do corte representado, uma vez que se encontram à mesma profundidade, as forças de pressão \(\vec{F}_p\) têm a mesma intensidade. Estas forças têm resultante nula e, por isso, não contribuem para a dinâmica do corpo.
Figura 1. À esquerda: um corpo cilídrico, de secção reta constante, encontra-se totalmente imerso num líquido; por simplicidade, admite-se que as bases do cilindro são horizontais. As setas verticais representam as forças de pressão que atuam na direção vertical; note-se que a força de pressão que atua na base inferior tem módulo superior á que atua na base superior. À direita: corte transversal do cilindro por um plano horizontal. As setas representam as forças de pressão que atuam na superfície lateral do cilindro. Em todos os pontos do corte representado, uma vez que se encontram à mesma profundidade, as forças de pressão \(\vec{F}_p\) têm a mesma intensidade. Estas forças têm resultante nula e, por isso, não contribuem para a dinâmica do corpo.

Consideremos um corpo cilíndrico, de massa \(m\), secção reta constante \(S\) e altura \(h\)", totalmente imerso num fluido incompressível, de densidade \(\rho\), como se representa na figura acima (esquerda). Segundo a direção vertical, o corpo está sujeito a forças de pressão na base superior e inferior. Segundo a direção horizontal, aforça de pressão aplicada à superfície lateral do corpo tm resultante nula. Sendo assim, a resultante de todas as forças de pressão que atuam no corpo só tem componente vertical:

\[\vec{I} = \vec{F}_A + \vec{F}_B\]


em que a distância vertical entre o ponto A e B corresponde ao comprimento do corpo.

Considerando positivo o sentido de baixo para cima, o módulo da resultante das forças de pressão é:

\[I = -F_A + F_B\]


Usando a Lei Fundamental da Hidrostática:


\[-\frac{F_A} {S} + \frac{F_B} {S} = \rho g h \]


obtemos a intensidade da impulsão que atua no corpo:

\[I = \rho g h S = \rho g V\]


em que \(V\) é o volume do corpo. Se o corpo flutuar, o volume a considerar é o da parte do corpo que está imersa no fluido.

A equação anterior expressa matematicamente a Lei de Arquimedes:


"Todo o corpo mergulhado num fluido recebe, da parte deste, uma impulsão vertical de baixo para cima e de intensidade igual ao valor do peso do colume de fluido deslocado pelo corpo."


Flutuação

Consideremos agora um sistema corpo-fluido num campo gravitacional. O corpo, de massa \(m\), volume \(V\) e densidade \(\rho_{corpo}\) está totalmente imerso no fluido de densidade \(\rho_{fluido}\). O corpo está sujeito apenas a duas forças: o peso e a impulsão.

  • O corpo afunda-se se o peso for maior que a impulsão:

    • \[ P > I \Leftrightarrow mg > \rho_{fluido} g V \Leftrightarrow \rho_{corpo} g V > \rho_{fluido} g V \Leftrightarrow \rho_{corpo} > \rho_{fluido} \]


  • O corpo fica em equilíbrio no seio do fluido se a impulsão for igual ao peso:

    • \[ P = I \Leftrightarrow \rho_{corpo} g V = \rho_{fluido} g V \Leftrightarrow \rho_{corpo} > \rho_{fluido} \]


  • O corpo flutua quando a força de impulsão é maior do que o peso. Nesse caso, o corpo, inicialmente imerso no líquido, é acelerado no sentido da superfície do fluido (esta aceleração não é uniforme, devido à ação da força de viscosidade do flúido, que dependen da velocidade com que o corpo se desloca). Na superfície livre do líquido, o corpo atinge o equilíbrio mecânico quando a parte imersa do seu volume \( V_i\) é tal que:

    • \[ I_i = P \Leftrightarrow \rho_{fluido} V_i = \rho_{corpo} V \]


    Como \( V_i < V \), para que a igualdade se mantenha tem que ser verdade que:


    \[ \rho_{fluido} > \rho_{corpo} \]