Caudal
📧
- Faculdade de Ciências da Universidade do Porto
Referência Ferreira, M., (2014) Caudal, Rev. Ciência Elem., V2(4):076
DOI http://doi.org/10.24927/rce2014.076
Palavras-chave Caudal;
Resumo
O caudal volumétrico (\( Q\)) é a quantidade de volume de um fluido que atravessa uma determinada área por unidade de tempo. Designa-se caudal mássico (\(Q_m\)) à massa que atravessa por unidade de tempo uma dada área.
Num fluido incompressível, de densidade \(\rho\), o caudal mássico é dado pelo produto da densidade do fluido pelo caudal:
\[ Q_m = \rho Q\]
Cálculo do Caudal num regime de escoamento laminar
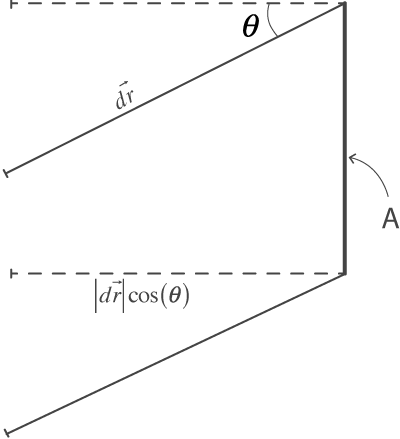
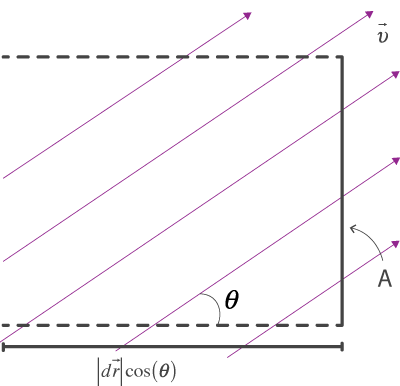
No que se segue, consideraremos um fluido em escoamento laminar ao longo de uma conduta e uma superfície plana, de área A. Na vizinhança da superfície plana considerada, a velocidade do fluido é \( \vec{v} \) e faz um ângulo \(\theta\) com a normal à superfície. Consideremos ainda um intervalo de tempo \( \Delta t \). O volume de fluido que atravessa a superfície no intervalo de tempo \( \Delta t \) é:
\[\Delta V = |\vec{v}| cos(\theta) A \Delta t\]
Por definição, o caudal volumétrico é dado pela expressão:
\[Q = \frac{\Delta V} {\Delta t} = |\vec{v}| cos(\theta) A\]
Este artigo já foi visualizado 8305 vezes.



