Argumento de um número complexo
📧
- Faculdade de Ciências da Universidade de Lisboa
Referência Ramos, F., (2014) Argumento de um número complexo, Rev. Ciência Elem., V2(4):079
DOI http://doi.org/10.24927/rce2014.079
Palavras-chave Argumento; número; complexo;
Resumo
Argumento de um número complexo não nulo, \(z = x + i y\), com \(x, \, y\) números reais não simultaneamente nulos, é qualquer número real \(\theta\) tal que \(\displaystyle \cos\,\theta=\frac{x} {|z|}\) e \(\displaystyle \sin\,\theta=\frac{y} {|z|}\), onde \(|z|=\sqrt{x^{2}+y^{2} }\) é o módulo do número complexo \(z\).
Escreve-se habitualmente \(\theta=\arg\left(z\right)\).
Geometricamente:
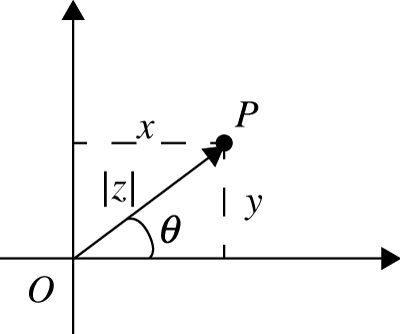
Onde \(\theta\) é a amplitude do ângulo, medida em radianos, de vértice na origem, \(O\), cujo lado origem é o semi-eixo real positivo e o lado extremidade é a semi-reta \(\dot{O}P\) em que \(P\) é o afixode z.
Nota
Decorre da definição anterior que para cada número complexo \(z\) não existe um argumento univocamente determinado pois, se \(\theta=\arg\left(z\right)\), também, \(\theta+2k\pi = \arg\left(z\right)\) para qualquer número inteiro \(k\).
O número complexo \(z = 0 \) tem argumento indeterminado, pois qualquer número real \(\theta\) pode ser um argumento para \(z = 0\).
Exemplo
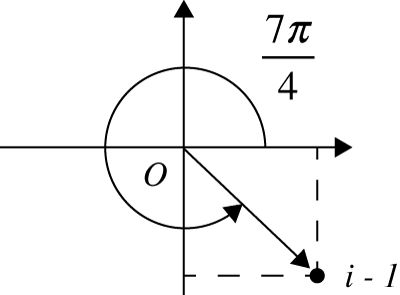
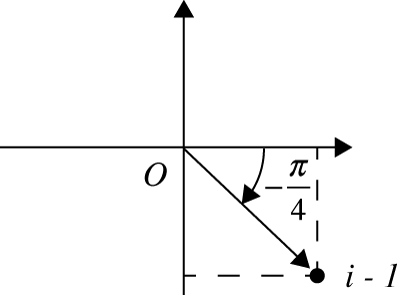
O complexo \(z=1-i\), tem por exemplo, os argumentos \(\displaystyle \theta_{1}=\frac{7\pi} {4}\),\(\displaystyle \theta_{2}=-\frac{\pi} {4}\), \(\displaystyle \theta_{3}=\frac{15\pi} {4}\), ou genericamente \(\displaystyle \theta =\frac{7\pi}{4} + 2k \pi\), onde \(k\) é qualquer número inteiro.
Geometricamente:
Este artigo já foi visualizado 4255 vezes.



