O legado dos fenómenos de fusão nuclear remonta a 1920 quando o astrónomo Sir Arthur Eddington (1882 – 1944) propõe a ocorrência de fusões nucleares nos seus modelos estelares. Contudo, apenas nos anos 30 é que a fusão nuclear é verificada experimentalmente.² Em 1932 a fusão de isótopos de hidrogénio é conseguida em laboratório e em 1939 o físico nuclear Hans Bethe (1906 – 2005) descreve os processos de fusão nuclear existentes nas estrelas (nucleossíntese estelar).

A fusão nuclear é um fenómeno incrivelmente difícil de ser provocado, exigindo temperaturas da ordem de muitos milhares de graus Celsius. No entanto, quando alcançado, liberta muito mais energia do que a que consome. A energia gigantesca necessária para ativar o processo de fusão nuclear deve-se, essencialmente, à barreira de forças electroestáticas entre os núcleos (carregados positivamente).

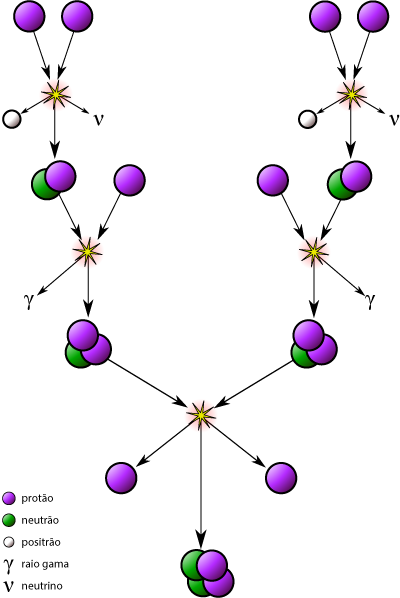
Uma das mais importantes cadeias de reações de fusão nuclear ocorre no Sol e estrelas idênticas que utilizam como “combustível” o seu hidrogénio produzindo hélio (ver figura 1). As equações que descrevem o processo exposto na figura 1 podem também ser escritas³

\[{}_1^1 H + {}_1^1 H \longrightarrow {}_1^2 H + e^+ + \nu + 0,42 MeV\]

\[{}_1^1 H + {}_1^2 H \longrightarrow {}_2^3 He + \gamma + 5,49 MeV\]

\[{}_2^3 He + {}_2^3 He \longrightarrow {}_2^4 He + _1^1 H + {}_1^1 H + 12,86 MeV\]

em que \({}_1^1 H\) é um protão, \({}_1^2 H\) é o deutério, \(e^+\) é um positrão (ou eletrão positivo), \(\nu\) é um neutrino (que não possui nem número atómico nem número de massa), \({}_2^3 He\) é o hélio-3, \(\gamma\) é um fotão gama e \({}_2^4 He\) é o isótopo mais estável do hélio (também denominado de partícula alfa).

Note-se que a libertação de energia neste processo está expressa em MeV/átomo em vez de kJ/mol, o que evidencia a enorme diferença entre as ordens de grandeza das energias envolvidas nas reações químicas e nas nucleares. Por exemplo, a combustão do gás propano debita 2220 J por cada mole de gás (3,60 x 10^-21 J/molécula de propano) que reage enquanto a anterior reação de fusão nuclear entre dois núcleos de hélio-3 com a formação de um núcleo de hélio-4 e dois protões debita 110 x 10¹² J por cada mole de átomos de hélio-4 formado (18 x 10^-11 J/átomo = 12,86 MeV/átomo).^‡

A escrita de equações que traduzem reações de fusão nucleares (tal como as de fissão nuclear) obedece a duas regras específicas⁵:

• Regra Z – A soma dos números atómicos, Z, das partículas reagentes é igual à soma dos números atómicos dos produtos de reação;
• Regra A – A soma dos números de massa, A, das partículas reagentes é igual à soma dos números de massa dos produtos da reação.

A mais importante e desejada aplicação da fusão nuclear reside na construção de reatores termonucleares de fusão. Todavia, apesar do gigantesco esforço mundial, a fusão nuclear controlada ainda não foi atingida. Embora algumas reações nucleares de fusão já tenham sido realizadas em condições laboratoriais, tais como³

\[{}_1^2 H + {}_1^3 H \longrightarrow {}_2^4 He + n + 17,6 MeV\]

\[{}_1^2 H + {}_1^2 H \longrightarrow {}_2^3 He + n + 3,2 MeV\]

\[{}_1^2 H + {}_1^2 H \longrightarrow {}_1^3 H + _1^1 H + 4,0 MeV\]

A principal dificuldade na obtenção de energia a partir da fusão nuclear reside no problema da contenção do material combustível a temperaturas bastante elevadas (suficientemente elevadas para ser possível suplantar a barreira electroestática) durante um intervalo de tempo considerável.³ Uma equipa internacional de cientistas está a colaborar na construção de um reator de fusão chamado International Thermonuclear Experimental Reator (ITER), que irá testar a viabilidade comercial da utilização da fusão nuclear.² Contudo, ainda há muito trabalho a ser realizado antes da energia proveniente da fusão nuclear poder ser comercializada.

‡ Como 1 eV = 1,6022 x 10^-19 J, 1 MeV/átomo corresponde a 9,65 x 10⁷ kJ/mol.⁶