Leis de Kepler
📧
- Faculdade de Ciências da Universidade do Porto
Referência Araújo, M., (2014) Leis de Kepler, Rev. Ciência Elem., V2(1):104
DOI http://doi.org/10.24927/rce2014.104
Palavras-chave Kepler; planetas; Sol; Newton;
Resumo
As leis de Kepler constituem uma base para a descrição do movimento dos planetas em torno do Sol. Foram descobertas originalmente por Johannes Kepler pela análise dos dados observacionais de Tycho Brahe, relativos à posição de alguns planetas do Sistema Solar. Posteriormente, Isaac Newton mostrou que as leis de Kepler podem ser deduzidas a partir das leis da Mecânica e da Lei da Gravitação Universal, para um sistema de dois corpos sujeitos a uma força central em que um deles, o astro diretor, tem uma massa muito superior à do outro, o astro dirigido.
Lei das órbitas
A órbita do astro dirigido em torno do astro diretor é uma elipse, da qual o astro diretor ocupa um dos focos. Em geral num sistema de dois corpos estes orbitam em torno do seu centro de massa. No entanto, quando um dos corpos tem uma massa muito maior que o outro, o centro de massa do sistema praticamente coincide com o centro do corpo de maior massa, pelo que se pode considerar que este está parado, e que o outro orbita em torno dele. A lei das órbitas aplica-se a estes sistemas, como é o caso do Sistema Solar ou de satélites que orbitam em torno de um planeta.
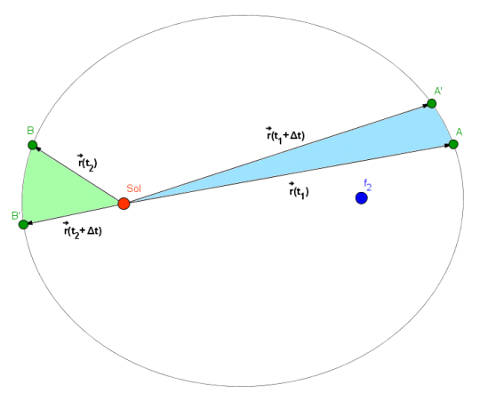
Lei das áreas
O vetor de posição de um corpo em relação ao astro diretor varre áreas iguais em intervalos de tempo iguais. Esta lei é uma consequência da conservação do momento angular do astro dirigido que se encontra sob a ação de uma força central que aponta sempre para o centro do astro diretor. Como a área varrida por unidade de tempo é constante e o corpo não está sempre à mesma distância do astro diretor, a sua velocidade varia, sendo máxima quando a distância entre os dois corpos é mínima, e mínima quando a distância é máxima.
Lei dos Períodos
A razão entre o cubo do semi-eixo maior da órbita de um planeta e o quadrado do respetivo período é uma constante:
\(\frac{T^2}{a^3} = K\)
A constante K é chamada constante de Kepler e é igual para todos os corpos que orbitam em torno do mesmo astro.
| Planeta | Período (anos) | Distância média ao Sol (UA) | Constante de Kepler | Erro relativo (%) |
|---|---|---|---|---|
| Mercúrio | 0,24085 | 0,387 | 1,001 | 0,08 |
| Vénus | 0,61520 | 0,723 | 1,001 | 0,1 |
| Terra | 1,00000 | 1,000 | 1,000 | - |
| Marte | 1,88071 | 1,524 | 0,999 | 0,07 |
| Júpiter | 11,85654 | 5,203 | 0,9981 | 0,2 |
| Saturno | 29,44750 | 9,537 | 0,9997 | 0,03 |
| Úrano | 84,01697 | 19,191 | 0,9987 | 0,1 |
| Neptuno | 164,79124 | 30,069 | 0,9989 | 0,1 |
| Satélite | Período (anos) | Distância média a Júpiter (UA) | Constante de Kepler |
|---|---|---|---|
| Io | 4,843E-03 | 2,82E-03 | 1,04E+03 |
| Europa | 9,722E-03 | 4,49E-03 | 1,05E+03 |
| Ganymede | 1,959E-02 | 7,15E-03 | 1,05E+03 |
| Callisto | 4,569E-02 | 1,26E-02 | 1,05E+03 |
Referências
- 1 Kepler, J., New Astronomy, Cambridge University Press, 1993.
- 2 Feymnan, R., Leighton, R. & Sands, M., The Feynman Lectures on Physics, Vol,. 1, Addison-Wesley Publishing, 1963.
- 3 Feynman, R., Goodstein, J. & Goodstein, D., A lição esquecida de Feynman, Gradiva, 1997.
- 4 Copernicus, N., Kepler, J., Galilei, G., Newton, I., Einstein, A. & Hawking, S., On the Shoulders of Giants, Running Press, 2002.
Este artigo já foi visualizado 9818 vezes.



