Lei dos senos
📧 , 📧
- * CMUP/ Universidade do Porto
- ɫ CMUP/ Universidade do Porto
Referência Tavares, J., Geraldo, A., (2014) Lei dos senos, Rev. Ciência Elem., V2(1):113
DOI http://doi.org/10.24927/rce2014.113
Palavras-chave Lei dos senos; triângulo; vértices; ângulos
Resumo
|
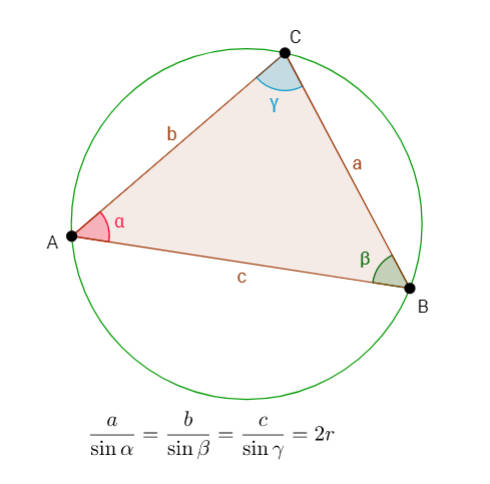
Consideremos um triângulo \(ABC\), como o representado na imagem ao lado. As notações para os vértices e para as medidas de lados e de ângulos internos são as indicadas. Nestas condições, a lei dos senos diz que: \(\displaystyle\frac{a}{\sin\alpha}=\displaystyle\frac{b}{\sin\beta}=\displaystyle\frac{c}{\sin\gamma}\) Podemos ainda ser mais específicos. Para isso, consideremos a circunferência circunscrita ao triângulo \(ABC\), e seja \(r\) o seu raio. Então \(\displaystyle\frac{a}{\sin\alpha}=\displaystyle\frac{b}{\sin\beta}=\displaystyle\frac{c}{\sin\gamma}=2r\) |
Demonstração
|
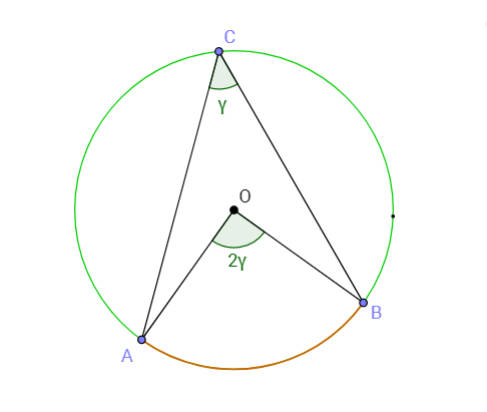
Para provar a lei dos senos, usamos o facto conhecido (Proposição 20 do livro III dos Elementos de Euclides) de que a medida de um ângulo inscrito numa circunferência (isto é, um ângulo cujo vértice está sobre a circunferência e os lados contêm duas cordas da circunferência), é igual a metade da medida do ângulo ao centro (ou arco) que subtende a mesma corda ou metade da amplitude do arco \(AB\). |
|
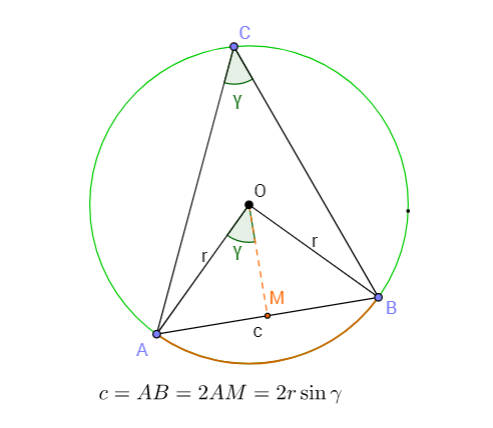
Consideremos de novo a circunferência circunscrita ao triângulo \(ABC\), e seja \(r\) o seu raio. Temos que: \(\angle AOB=2\angle ACB=2\gamma\). Baixemos, a partir de \(O\), a perpendicular que bisseta o lado \(AB\). Temos então que \(\sin\gamma=\displaystyle \frac{c}{2}r\) o que implica que \(\displaystyle \frac{c}{\sin\gamma}=2r=\mbox{constante}\) que é uma constante, constante esta que é independente de \(c\) e \(\gamma\). Fazendo exatamente o mesmo procedimento para os dois outros lados e ângulos internos, obtemo \(\displaystyle\frac{a}{\sin\alpha}=\displaystyle\frac{b}{\sin\beta}=\displaystyle\frac{c}{\sin\gamma}=2r\) como se pretendia. |
Aplicações
Aplicação 1
|
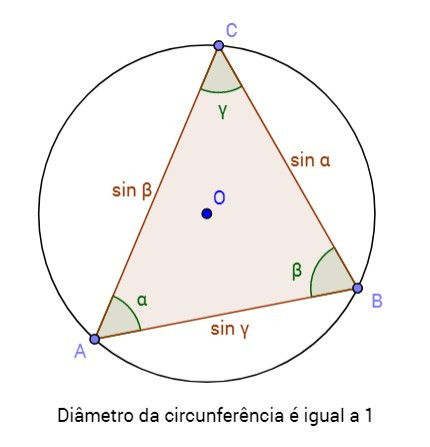
Num triângulo inscrito numa circunferência de diâmetro igual a 1, o comprimento de cada lado é igual ao seno do ângulo oposto. Com efeito, neste caso, a lei do senos diz que \(\displaystyle\frac{a}{\sin\alpha}=\displaystyle\frac{b}{\sin\beta}=\displaystyle\frac{c}{\sin\gamma}=1\) donde se deduz que \(a=\sin\alpha, b=\sin\beta\) e \(c=\sin\gamma\). |
Fórmulas de duplicação
|
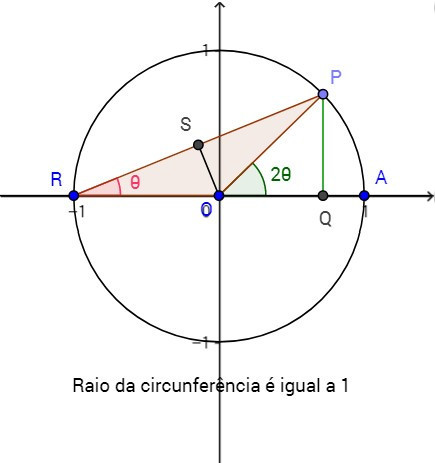
Consideremos o triângulo \(ROP\) inscrito numa circunferência de raio igual a 1, que se ilustra na imagem ao lado. Se \(\angle AOP=2\theta\), então \(\angle ARP=\theta\). Aplicando a lei dos senos ao triângulo \(ROP\), obtemos \(\displaystyle \frac{RP}{\sin(180º-2\theta)}=\displaystyle \frac{OP}{\sin\theta}=\displaystyle \frac{1}{\sin\theta}\) uma vez que \(OP=1\), donde se deduz que \(\sin 2\theta=RP\, \sin \theta\), uma vez que \(\sin(180º-2\theta)=\sin\theta\). Por outro lado, do triângulo \(RSO\), retângulo em \(S\), obtemos que \(\cos\theta=\displaystyle \frac{RS}{RO}=\displaystyle \frac{(RP/2)}{1}=\displaystyle \frac{RP}{2}\), o que implica que \(RP=2\cos\theta\). Substituindo \(RP\) na fórmula \(\sin 2\theta=RP\, \sin \theta\), acima deduzida, obtemos uma fórmula do seno do ângulo duplo: \(\sin 2\theta=2\sin\theta\cos\theta\) |
Fazendo um raciocínio análogo, aplicado agora ao triângulo \(RQP\), retângulo em \(Q\), obtemos as fórmulas do cosseno do ângulo duplo:
\(\cos 2\theta=2\cos^2\theta -1 = \cos^2\theta-\sin^2\theta\)
Este artigo já foi visualizado 7021 vezes.



