Se representarmos os dados por $x_{1}, x_{2},..., x_{n}$, a característica amostral média representa-se por $\bar{x}$ e é igual a

$\bar{x}=\frac{\sum\limits_{i=1}^{n}x_{i}}{n}$

É uma medida de localização do centro (ou de tendência central) da distribuição dos dados. Apesar de ser uma medida muito utilizada, tem que se ter as devidas cautelas, pois a média é muito sensível a valores muito grandes ou muito pequenos, dizendo-se que é uma medida pouco resistente.

Por exemplo o conjunto de dados

$1 \quad 1,2 \quad 1,5 \quad 1,7 \quad 1,8 \quad 1,9 \quad 2 \quad 2,3 \quad 2,5 \quad 2,6 \quad 3$

tem média igual a 2,0. No entanto se subtituirmos o 3 por um 10, já a média virá igual a 2,6.

A média dá uma boa indicação do centro da amostra quando a distribuição dos dados for aproximadamente simétrica.

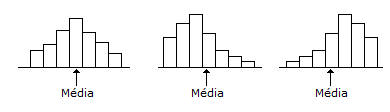
No histograma do lado esquerdo temos uma figura aproximadamente simétrica, pelo que o centro está bem definido. No histograma do centro o enviesamento para a direita provoca uma deslocação da média para a direita; finalmente no histograma da direita o enviesamento para a esquerda provoca uma deslocação da média para a esquerda.

Chama-se a atenção para que para dados de tipo qualitativo não tem sentido calcular a média, mesmo que esses dados sejam números. Se, por exemplo, temos um conjunto de 1’s e 2’s para representar as categorias feminino e masculino da variável Sexo, não tem qualquer sentido calcular a média daquele conjunto de dados.

A caraterística populacional ou parâmetro que corresponde à caraterística amostral ou estatística média, é o valor médio.

Quando se pretender estimar o parâmetro valor médio de uma variável aleatória, recolhe-se uma amostra de valores assumidos por essa variável e utiliza-se como estimativa a média.