Este tipo de representação é muito útil, pois permite realçar algumas propriedades entre os dados, nomeadamente no que diz respeito ao tipo de associação entre os x's e os y's.

Consideremos o seguinte conjunto de dados bivariados que representam as idades de 14 casais (GRAÇA MARTINS e PONTE (2010))

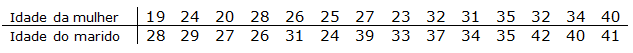
Representámos num sistema de eixos coordenados os pontos de coordenadas (Idade da mulher, Idade do marido), como se apresenta a seguir:

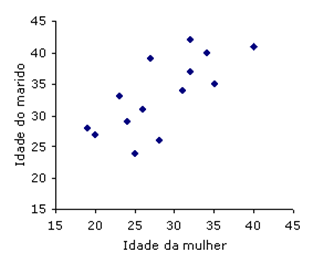
No diagrama de dispersão anterior, apercebemo-nos que, de um modo geral, à medida que a idade da mulher aumenta, também aumenta a idade do marido. Dizemos de um modo geral, porque nem sempre isso acontece, mas existe tendência a que mulheres mais velhas estejam casadas com homens mais velhos. Neste exemplo, a nuvem de pontos, embora um pouco dispersa, apresenta uma forma alongada, que pode ser representada por uma reta com declive positivo:

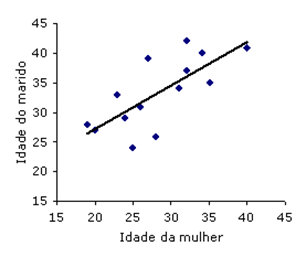
Quanto mais perto os pontos se dispuserem ao longo de uma reta, maior será o grau de associação entre as duas variáveis. Essa associação diz-se positiva, se a reta tiver declive positivo. O exemplo anterior é um caso de uma associação positiva. A associação será negativa, se a reta tiver declive negativo. Neste caso, quanto maior for o valor de uma das variáveis, menor será, de um modo geral, o valor da outra variável. O grau da associação linear é expresso numericamente pelo coeficiente de correlação amostral de Pearson ou pelo seu quadrado, o coeficiente de determinação.