Ciclotrão
📧
- Faculdade de Ciências da Universidade do Porto
Referência Ferreira, M., (2014) Ciclotrão, Rev. Ciência Elem., V2(4):254
DOI http://doi.org/10.24927/rce2014.254
Palavras-chave Ciclotrão; partículas; energia;
Resumo
O ciclotrão é um instrumento utilizado para acelerar partículas carregadas até altas energias cinéticas.
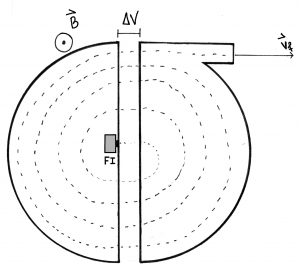
O ciclotrão é constituído por dois condutores semi-circulares ocos mantidos no vácuo e dispostos de maneira a formar dois D separados (ver figura 1). Entre estas duas peças aplica-se uma diferença de potencial alternada, cuja frequência é ajustada de modo a que, quando as partículas alcançam a separação entre os dois D, estas sejam aceleradas no mesmo sentido da sua velocidade. Na região dos D 's existe um campo magnético uniforme, independente do tempo, cuja direção é perpendicular ao plano dos D 's.
Consideremos, por simplicidade, o caso não relativista.
Uma partícula eletricamente carregada em movimento, sujeita à ação de um campo magnético uniforme perpendicular à sua velocidade, descreve uma trajetória circular cujo período é independente da velocidade:
\(T = \frac{2 \pi m}{q B}\)
Os iões produzidos pela fonte, FI, colocada no centro do sistema formado pelos dois D 's, são acelerados pela diferença de potencial entre os D e, ao entrarem num deles, descrevem uma trajetória semi-circular até atingir, ao fim do intervalo de tempo \(\frac{T}{2}\) , a separação entre os D. Entretanto, a diferença de potencial entre os D mudou de sentido e os iões são acelerados, aumentando a sua energia cinética. No segundo D, o raio da trajetória semicircular é maior do que no primeiro, porque a velocidade da partícula é agora maior do que anteriormente. A partícula volta a alcançar a separação entre os D, passado o intervalo de tempo \(\frac{T}{2}\) desde a entrada no segundo D. Se a frequência de oscilação do potencial elétrico for \(f = \frac{q B}{m \pi}\) , há uma alternância do sentido da diferença de potencial aceleradora cada \(\frac{T}{2}\) segundos, garantindo que a partícula será acelerada no sentido da sua velocidade, ou seja, havendo sempre um aumento da sua energia cinética, no valor de \(q \Delta V \).
O processo descrito atrás repete-se várias vezes até que uma placa defletora desvia a partícula para fora do sistema. A energia cinética da partícula que sai do ciclotrão está relacionada com o raio máximo que esta descreve antes de sair do sistema: Sabe-se que o raio de uma partícula de carga \(q\) sujeita ao efeito de um campo magnético constante é \(r = \frac{m v}{q B}\) ,
então \(m v^2 = \frac{q^2 B^2}{m} r^2\) e
\( E_{cin} = \frac{1}{2} \frac{q^2 B^2}{m} R_{max}^2\).
Aumento relativista da massa
velocidade tal que os efeitos relativistas se tornam apreciáveis, a sua massa efetiva vai aumentar e vai depender da velocidade a que se movimenta. Por essa razão, o tempo que demora a percorrer o a trajetória circular vai deixar de ser independente da sua velocidade:
\(T(v) = \frac{2 \pi m(v)}{q B}\)
em que \( m(v) = \gamma m_0\)
em que \(m_0\) é a massa de repouso da partícula e \(\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2} } }\) o fator de Lorentz.
A sincronização que havia no regime não-relativista entre o movimento da partícula e as oscilações da diferença de potencial deixa de existir. Diz-se que a partícula e a oscilação do potencial estão desfasados. Para terminar, chama-se a atenção de que uma carga acelerada perde energia por radiação.
Este artigo já foi visualizado 3865 vezes.



