Há vários processos para calcular os quartis, que não conduzem necessariamente aos mesmos valores, mas a valores próximos, desde que a amostra tenha uma dimensão razoável, que é a situação de interesse em Estatística, em que se procura resumir a informação contida nos dados, através de algumas medidas.

Uma metodologia que pode ser seguida para obter os quartis é a seguinte:

• Ordenar os dados por ordem crescente e calcular a mediana;
• O 1.º quartil, Q₁, é a mediana dos dados que ficam para a esquerda da mediana;
• O 3.º quartil, Q₃, é a mediana dos dados que ficam para a direita da mediana.

Quando o número de dados é ímpar, o processo seguido, por exemplo, em MANN (1995) ou MOORE (1996), considera cada uma das partes em que fica dividida a amostra pela mediana, sem a incluir. Por exemplo,

Esta metodologia não é seguida por outros autores, como por exemplo DE VEAUX et al. (2004) que inclui a mediana nas duas partes. Assim, o 1º e 3º quartis viriam, no caso do exemplo anterior

No caso do número de dados ser par, 2n, com n ∈ℕ, não há ambiguidade na definição dos quartis que serão sempre as medianas de conjuntos de dados com n elementos.

Do mesmo modo que a mediana, também se podem obter os quartis a partir das tabelas de frequências com os dados agrupados.

Do mesmo modo que a mediana, também se podem obter os quartis a partir das tabelas de frequências com os dados agrupados.

À diferença entre o 3º quartil e o 1º quartil dá-se o nome de amplitude interquartil, que é uma medida da variabilidade ou dispersão (medidas de dispersão) entre os dados.

Os quartis são utilizados na construção do diagrama de extremos e quartis e do diagrama caixa de bigodes.

A característica populacional que corresponde à característica amostral quartil, também se denomina quartil e determina-se da mesma maneira (para uma população finita). Depende do contexto saber se nos estamos a referir à estatística - quartil amostral, ou ao parâmetro - quartil populacional.

Nota:

Sendo os quartis um caso especial dos quantis, podem-se utilizar as fórmulas aí consideradas para a sua obtenção. Um método mais elaborado para o cálculo dos quartis (Murteira, 2002), será descrito a seguir, por ser também o método utilizado na folha de Excel. Neste processo, começa por se considerar para a determinação do 1º e 3º quartis, respetivamente as “posições” n+34$\frac{n+3}{4}$ e $\frac{3n+1}{4}$ (1). No que respeita o 1º quartil, Q₁, se $\frac{n+3}{4}$ for inteiro, então Q₁ será a observação de ordem $\frac{n+3}{4}=k$, na amostra ordenada. Se $\frac{n+3}{4}$ não for inteiro, seja $\frac{n+3}{4}=k+\varepsilon$, em que representamos por $\varepsilon$ a parte decimal (igual a 0,25, 0,5 ou 0,75). Para obter Q₁ considera-se uma interpolação linear, fazendo uma média ponderada entre a observação de ordem $k$ e a observação de ordem $(k + 1)$: Q1=observação de ordem $k+\varepsilon$ (observação de ordem $(k + 1)$ − observação de ordem $k$)

O raciocínio utilizado para obter o 3º quartil, Q₃, é idêntico ao descrito para a determinação do 1º quartil, considerando agora a posição $\frac{3n+1}{4}$ em vez de $\frac{3n+1}{4}$.

Adiantamos que quando a dimensão da amostra é ímpar, este processo conduz aos mesmos resultados que o considerado por DE VEAUX et al. (2004), em que se considera os quartis como as medianas de cada uma das partes em que fica dividida a amostra, incluindo a mediana em cada uma dessas partes.

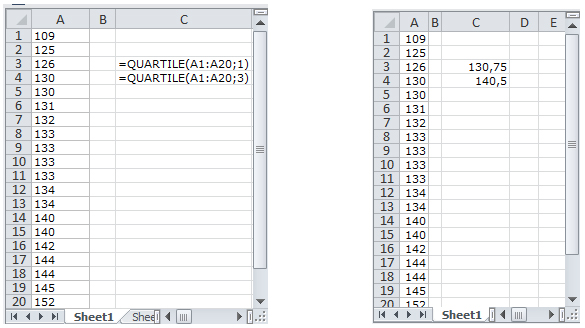
Considere-se, por exemplo, os seguintes dados correspondentes às alturas em cm, dos 20 alunos de uma turma (a amostra já se encontra ordenada):

De acordo com a metodologia descrita anteriormente, o 1º quartil e o 3º quartil estão, respetivamente, nas “posições” 5,75 e 15,25 pelo que realizando as interpolações lineares, tem-se

Na folha de Excel obtém-se:

(1) Dada uma amostra de dimensão n, ordenada, considera-se que a “posição” da mediana é definida por $\frac{n+1}{2}$. Quando n é ímpar, a mediana corresponde à observação de ordem $\frac{n+1}{2}$. Quando n é par é a semissoma (interpolação linear) das observações de ordem $\frac{n}{2}$ e $\frac{n}{2}+1$. Para definir o 1º quartil considera-se a “posição” definida por $\frac{posic\tilde{a}o\; da\; mediana+1}{2}=\frac{\frac{n+1}{2}+1}{2}=\frac{n+3}{4}$.

Para obter a “posição” do 3º quartil basta considerar $n-\frac{n+3}{4}+1=\frac{3n+1}{4}$. Da mesma forma que se calcula a mediana, se $\frac{n+3}{4}$ e $\frac{3n+1}{4}$ são inteiros, os quartis são as observações que correspondem a essas ordens. Caso contrário faz-se uma interpolação linear entre as observações correspondentes às ordens adjacentes.

Repare-se que estamos aqui a generalizar o conceito de “posição” para valores não necessariamente inteiros.