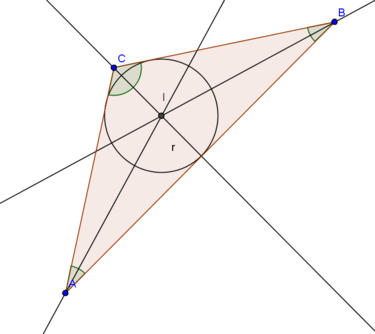
Incentro é o ponto de interseção das bissetrizes de um triângulo.

Figura 1. \( I\) é o incentro de \( [ABC]\).

Notas

Dado um qualquer triângulo \( [ABC]\), o incentro \( I\) está equidistante dos lados \( [AB]\), \( [BC]\) e \( [AC]\), a uma distância \( r\).

A circunferência de centro em \( I\) e raio \( r\), tangente aos três lados do triângulo, é a circunferência inscrita no triângulo.

O incentro de um triângulo é sempre um ponto no interior do triângulo.


Sugestões

Distinga incentro, circuncentro, baricentro e ortocentro de um triângulo:

Verifique as posições relativas destes pontos, deslocando os vértices \( A\), \( B\) e/ou \( C\) e apresentando, respetivamente, as bissetrizes, mediatrizes, medianas e alturas dos diferentes triângulos.


Aplicação interativa