Polígonos regulares
📧 , 📧
- * CMUP/ Universidade do Porto
- ɫ CMUP/ Universidade do Porto
Referência Tavares, J., Geraldo, A., (2014) Polígonos regulares, Rev. Ciência Elem., V2(3):323
DOI http://doi.org/10.24927/rce2014.323
Palavras-chave Polígonos; ângulos;
Resumo
Um polígono diz-se regular se tiver todos os seus lados e ângulos iguais.
Circunferências inscrita e circunscrita
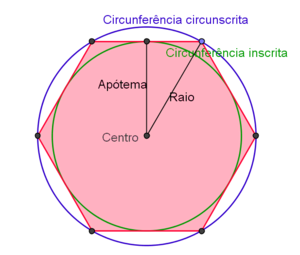
Cada polígono regular \({\mathcal{P}}_n\), de n lados, admite uma única circunferência circunscrita \(\mathcal{C}\), que passa em todos os n vértices do polígono. O centro da circunferência \(\mathcal{C}\) chama-se o centro do polígono \({\mathcal{P}}_n\).
Cada polígono regular \({\mathcal{P}}_n\), de n lados, admite uma única circunferência inscrita \(\mathcal{I}\), que é tangente a cada um dos lados do polígono. O ponto de tangência com um lado é o ponto médio desse lado. O centro da circunferência \(\mathcal{I}\) coincide com o centro do polígono \({\mathcal{P}}_n\).
O raio da circunferência circunscrita \(\mathcal{C}\) chama-se o raio do polígono \({\mathcal{P}}_n\), enquanto que o raio da circunferência inscrita \(\mathcal{I}\) chama-se o apótema do polígono \({\mathcal{P}}_n\).
Soma dos ângulos externos e internos
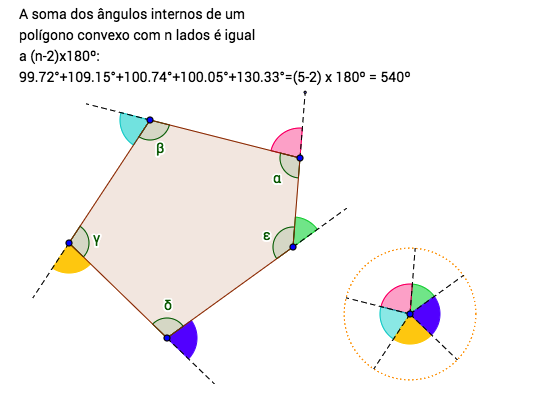
A soma das medidas dos ângulos externos \(\theta_i,\, i=1,...,n\) de um polígono convexo (regular ou não) de n lados, é igual a 360º ou \(2\pi\) radianos. A prova está sugerida no applett ao lado cuja interpretação é clara.

Como, em cada vértice \(i=1,...,n\), de um polígono convexo (regular ou não) de n lados, cada ângulo interno \(\alpha_i\) é igual a (180º - medida do correspondente ângulo externo \(\theta_i\), vem que
\(\begin{array}{lll} \displaystyle \sum_{i=1}^n\alpha_i & = & \displaystyle \sum_{i=1}^n (180º-\theta_i) \\ &=& n 180º-\displaystyle \sum_{i=1}^n \theta_i \\ &=& n 180º-360º =(n-2) \, 180º \end{array}\)
Concluindo: a soma dos ângulos internos \(\alpha_i,\, i=1,...,n\) de um polígono convexo (regular ou não) de n lados, é igual a \((n-2) \, 180º\) ou \((n-2) \,\pi\) radianos.
Perímetro e área
Seja \({\mathcal{P}}_n\) um polígono regular de raio r, com de n lados. O raio da circunferência circunscrita é pois igual a r. A que é igual o comprimento \(a_n\) do lado de polígono?
Pela figura ao lado, vemos que \(\displaystyle\frac{a_n}{2}=r \sin\displaystyle\frac{\pi}{n}\) ( o triângulo ACE é retângulo) e portanto
\(\mbox{Perímetro}({\mathcal{P}}_n) = 2nr \sin\displaystyle\frac{\pi}{n}\)
Por outro lado, o apótema CE de \({\mathcal{P}}_n\) é igual a \(r \cos\displaystyle\frac{\pi}{n}\). Portanto, a área do triângulo ACB é igual a \(\displaystyle\frac{\left(\mbox{base} \times \mbox{altura}\right)}{2}\), isto é, é igual a \(\displaystyle\frac{a_n\times \mbox{apótema}}{2}\) ou, ainda, \(r^2 \sin\displaystyle\frac{\pi}{n} \cos\displaystyle\frac{\pi}{n}=\displaystyle\frac{1}{2} r^2\sin\left(\displaystyle\frac{2\pi}{n}\right)\).
Como existem ao todo n triângulos iguais que preenchem o polígono dado, a sua área é
\(\mbox{Área}({\mathcal{P}}_n) = \displaystyle\frac{1}{2}n r^2\sin\left(\displaystyle\frac{2\pi}{n}\right)\).

Este artigo já foi visualizado 3584 vezes.



