O perímetro de uma circunferência \(\mathcal{C}\) de raio r, pode ser calculado como limite dos perímetros de duas sequências de polígonos regulares, a primeira com polígonos regulares inscritos em \(\mathcal{C}\) e a segunda com polígonos regulares circunscritos a \(\mathcal{C}\), à medida que o número de lados n aumenta para \(\infty\), como mostra o applet.

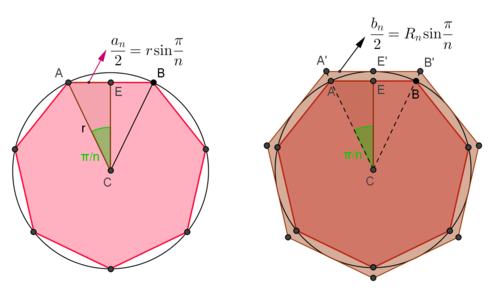
Seja \(p_n\) o perímetro de um polígono regular com n lados, cada um com comprimento \(a_n\), inscrito em \(\mathcal{C}\), e \(P_n\) o perímetro de um polígono regular com n lados, cada um com comprimento \(b_n\), circunscrito a \(\mathcal{C}\). Portanto, \(p_n=n a_n\) e \(P_n=n b_n\).

As figuras (ilustram o caso n = 7) permitem deduzir facilmente que \(a_n= 2r\sin\displaystyle\frac{\pi}{n}\) e que \(b_n= 2R_n\sin\displaystyle\frac{\pi}{n}\), onde \(R_n=CA'\) é o raio do polígono circunscrito, atendendo a que o triângulo ACE é retângulo

É claro que

• \(\displaystyle\lim_{n\to\infty}R_n=r\)
• a sucessão de perímetros \((p_n)_n\) é crescente
• a sucessão de perímetros \((P_n)_n\) é decrescente
• \(p_n\leq P_n\)

Assim ambos os limites \(\displaystyle\lim_{n\to\infty}p_n\) e \(\displaystyle\lim_{n\to\infty}P_n\) existam e são iguais:

\(\mbox{perímetro da circunferência}\, \mathcal{C} =\displaystyle\lim_{n\to\infty}p_n =\displaystyle\lim_{n\to\infty}P_n\)

De facto, usando o limite conhecido \(\displaystyle\lim_{x\to 0}\displaystyle\frac{\sin x}{x}=1\), podemos provar que os limites acima referidos são ambos iguais a \(2\pi r\), como seria de esperar.