Semelhança de triângulos
📧 , 📧
- * Faculdade de Ciências da Universidade do Porto
- ɫ CMUP/ Universidade do Porto
Referência Tavares, J.N., Geraldo, A., (2015) Semelhança de triângulos, Rev. Ciência Elem., V3(1):015
DOI http://doi.org/10.24927/rce2015.015
Palavras-chave Semelhança; triângulos;
Resumo
Definição
Na Figura 1 podemos ver uma correspondência entre os vértices de dois triângulos no plano, [ABC] e [AʹBʹCʹ].
Esta faz corresponder os pontos A, B e C aos pontos A', B' e C', respetivamente, assim como os ângulos α, β e γ; aos ângulos α', β' e γ', respetivamente.
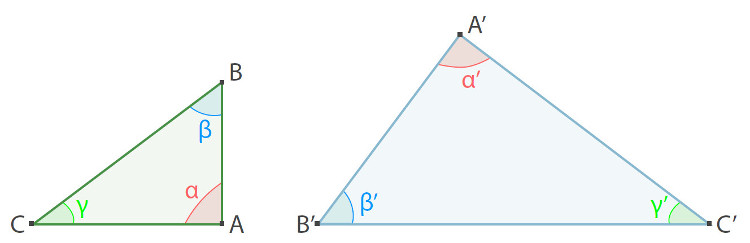
Dizemos que dois triângulos são semelhantes se essa correspondência entre os vértices for de tal modo que:
- os ângulos correspondentes são geometricamente iguais;
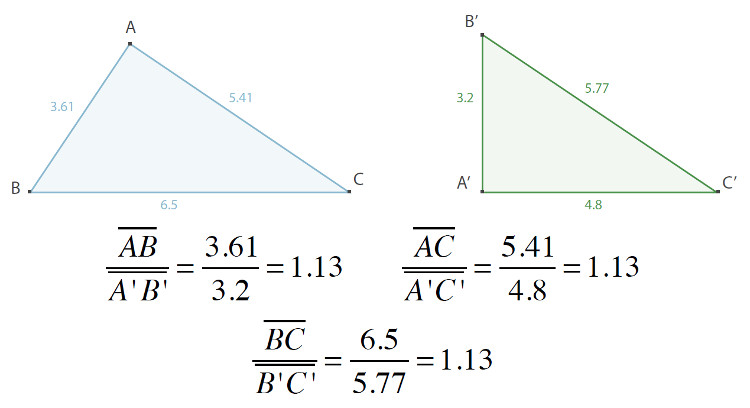
- e os lados correspondentes são diretamente proporcionais, ou seja,
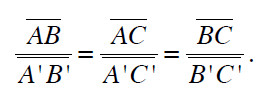
Nota — os lados de dois triângulos são proporcionais se existir proporcionalidade direta entre os seus comprimentos, ou seja, se o quociente entre os comprimentos dos lados correspondentes dos triângulos for sempre constante.
Critérios de semelhança de triângulos
- Critério AA
Dois quaisquer triângulos são semelhantes se tiverem dois ângulos correspondentes geometricamente iguais (o terceiro ângulo é necessariamente igual, pois a soma dos ângulos internos de um triângulo é sempre igual a 180°).
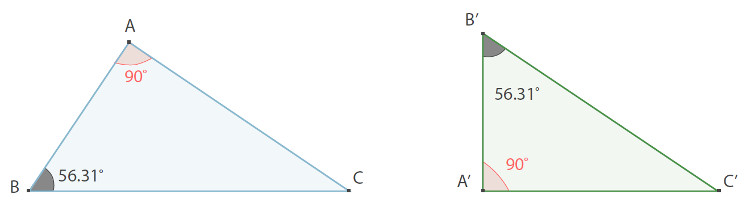
- Critério LAL
Dois quaisquer triângulos são semelhantes se tiverem dois lados correspondentes diretamente proporcionais e o ângulo por eles formado for igual.
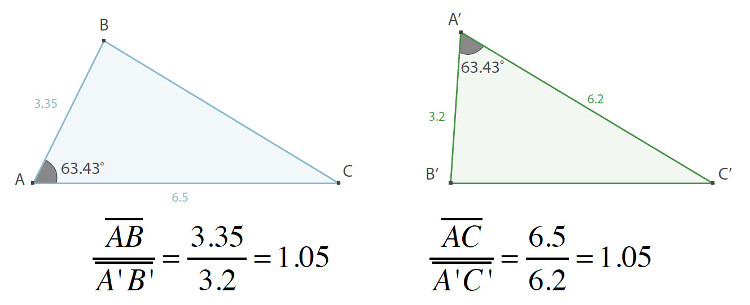
- Critério LLL
Dois quaisquer triângulos são semelhantes se tiverem os três lados correspondentes diretamente proporcionais.
Este artigo já foi visualizado 33305 vezes.



