Suponhamos que num ponto A, localizado na posição \(\overrightarrow{r}\)_A, se coloca uma outra carga pontual q. Esta carga fica sujeita a uma força de interação elétrica, que é descrita pela Lei de Coulomb:

\(\overrightarrow{F}{(r)} \frac{1}{4πε_0} \frac{qQ}{(r^2)}\hat{r}\)

Note-se que esta força depende da posição da carga q e da distância entre as duas cargas. Agora, suponhamos que a carga q é transportada para um ponto B, cuja posição é \(\overrightarrow{r}\)_B, sob ação de uma força externa, num processo quase estático. Nestas condições, a força externa é simétrica à força elétrica que atua na carga q. Mostra-se que o trabalho realizado pela força externa no transporte da carga q entre as posições A e B não depende do trajeto seguido pela carga q, dependendo apenas das posições inicial e final. O valor do trabalho realizado pela força externa é:

\(W = \frac{Qq}{4πε_0} \left(\frac{1}{r_A}-\frac{1}{r_B}\right)\)

Define-se a diferença de potencial elétrica entre os pontos A e B como sendo o trabalho realizado pela força externa por unidade de carga transportada:

\(ΔV = \frac{W}{q}=\frac{Q}{4πε_0} \left(\frac{1}{r_A}-\frac{1}{r_B}\right)\)

O potencial num ponto A do campo elétrico criado pela carga pontual Q, localizada na origem do referencial, é igual ao trabalho realizado pela força externa no transporte da carga q desde o infinito até ao ponto A:

\(V(A) = \frac{W}{q}=\frac{Q}{4πε_0}\frac{1}{r_A}\)

Consideremos agora um sistema formado por N cargas pontuais, de valores Q₁, Q₂, ..., Q_N, localizadas nos pontos \(\overrightarrow{r}\)₁, \(\overrightarrow{r}\)₂, ..., \(\overrightarrow{r}\)_N, respetivamente. Uma vez que a força elétrica satisfaz o Princípio da Sobreposição Linear, o potencial elétrico num dado ponto do espaço é igual à soma dos potenciais criados pelas diferentes cargas presentes:

\(V(r) = \frac{Q_1}{4 \pi \epsilon_0} \frac{1}{|\overrightarrow {r} - \overrightarrow {r}_1|} + \frac{Q_2}{4 \pi\epsilon_0} \frac{1}{|\overrightarrow {r} - \overrightarrow {r}_2|} + ... + \frac{Q_N}{4 \pi \epsilon_0} \frac{1}{|\overrightarrow {r} - \overrightarrow {r}_N|}\)

A unidade SI de potencial elétrico é o volt (V). A diferença de potencial de 1V entre dois pontos de um campo elétrico corresponde ao trabalho de 1J no transporte de +1C de carga entre esses dois pontos.
 

Superfícies Equipotenciais
As superfícies equipotenciais são o lugar geométrico dos pontos onde o potencial elétrico é constante. No caso de uma carga pontual, o potencial é o mesmo em todos os pontos equidistantes da carga e, por isso, as superfícies equipotenciais são superfícies esféricas concêntricas com a carga. Se a carga criadora do potencial for positiva (negativa), o potencial num dado ponto do espaço decresce (aumenta) à medida que a distância entre o ponto considerado e a carga aumenta. As figuras seguintes ilustram o que se afirmou. Note-se que as linhas de campo elétrico (sendo radiais) são normais às superfícies equipotenciais nos pontos de interseção, e o campo tem o sentido dos potenciais decrescentes. Esta propriedade geométrica entre linhas de campo e superfícies equipotenciais é geral. No caso em que o campo elétrico é uniforme, as superfícies equipotenciais são planos perpendiculares à direção do campo elétrico.

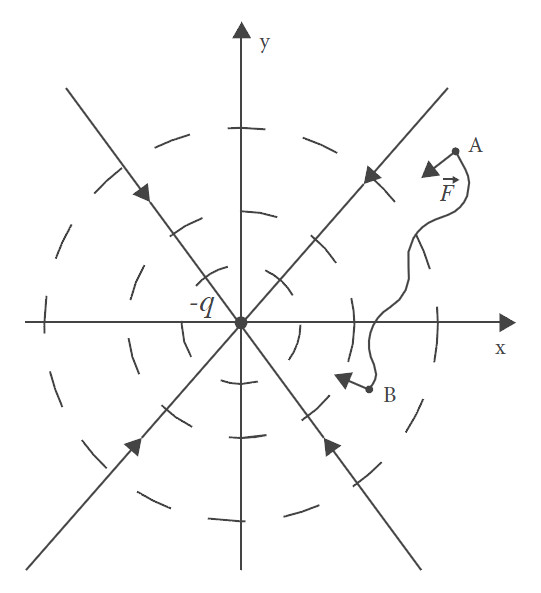
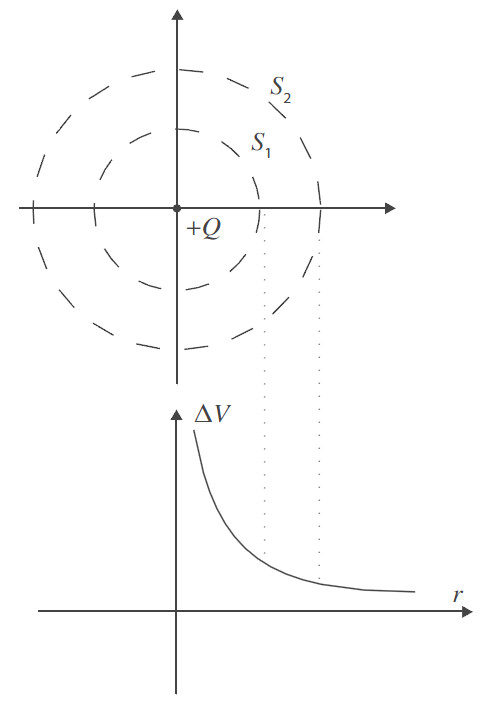
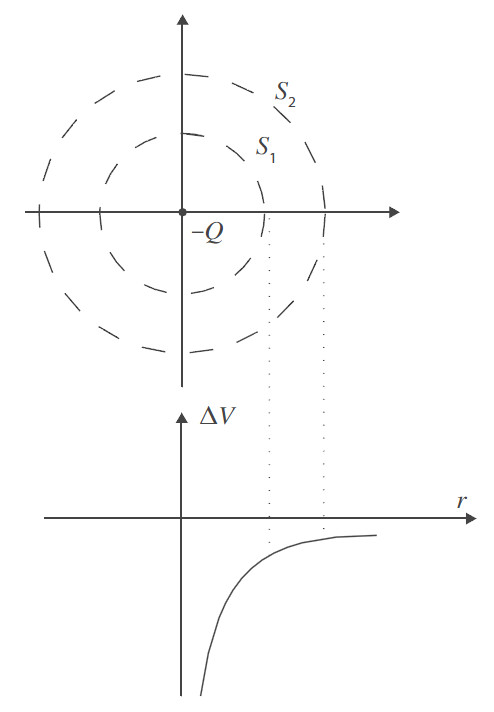
Uma forma simples de mostrar que as linhas de campo são perpendiculares às superfícies equipotenciais nos pontos de interseção, é considerar o trabalho realizado pela força elétrica no transporte de uma carga q, seguindo um percurso totalmente contido numa superfície equipotencial, de um campo elétrico uniforme. Nesta condição, mover a carga q ao longo da superfície equipotencial implica que o campo elétrico realize trabalho nulo. Assim, recordando que o trabalho de uma força constante é:

\(W = \overrightarrow{F} \bullet \overrightarrow{d} =|\overrightarrow{F}| |\overrightarrow{d}| \cos \theta\)

para que o trabalho realizado seja nulo, o ângulo entre a força elétrica e o deslocamento da carga q tem que ser 90°. Então, como a força elétrica tem a direção que o campo elétrico, conclui-se que a direção do campo elétrico faz um ângulo de 90° com a superfície equipotencial. Uma vez que o campo elétrico é sempre tangente às linhas de campo, as superfícies equipotencias são representadas perpendicularmente às linhas de campo.