Energia radiante
A energia total emitida, transferida ou recebida, num processo radiativo, é designada energia radiante, \(Q_{e}\). A unidade SI correspondente é o joule (J).
 

Potência ou fluxo radiante
A potência radiante (símbolo: Φe) é definida como a potência total de radiação emitida por uma fonte, transmitida através de uma superfície ou incidente sobre uma superfície. Medese em watts (W) e é dada por:


\( \phi_e=\frac{dQ_e}{dt}\)


A potência radiante caracteriza a emissão de uma fonte de radiação eletromagnética através de um número, apenas, não fornecendo qualquer informação sobre a distribuição espetral ou direcional da radiação da fonte.

As unidades de todas as grandezas radiométricas são baseadas no Watt.


Figura 1. A potência radiante de uma fonte luminosa corresponde a toda a radiação emitida por unidade de tempo.
Figura 1. A potência radiante de uma fonte luminosa corresponde a toda a radiação emitida por unidade de tempo.

Irradiância
A irradiância (símbolo: \(E_{e}\)) representa a quantidade de potência radiante que incide sobre uma superfície, real ou imaginária, por unidade de área. A unidade de irradiância é o W m-2.

Um elemento de superfície de área dA recebe uma potência radiante dΦe = \(E_{e}\) dA. Tem-se então:


\(E_e=\frac{d\phi_e} {dA}\)


Consideremos o caso simples de um feixe de radiação colimado incidente sobre uma superfície plana (Figura 2). Seja Φe a potência radiante do feixe e θ o ângulo entre ele e a normal à superfície. Seja \(A_{0}\) a área da secção reta do feixe. A área da superfície recetora iluminada pelo feixe é A(θ) = \(A_{0}\)/cos(θ) e a irradiância é dada por:


\(E_e(\theta)=\frac{\phi_e} {A(\theta)}=\left(\frac{\phi_e} {A_0}\right)\cos(\theta)=E_e(0)\cos(\theta)\)



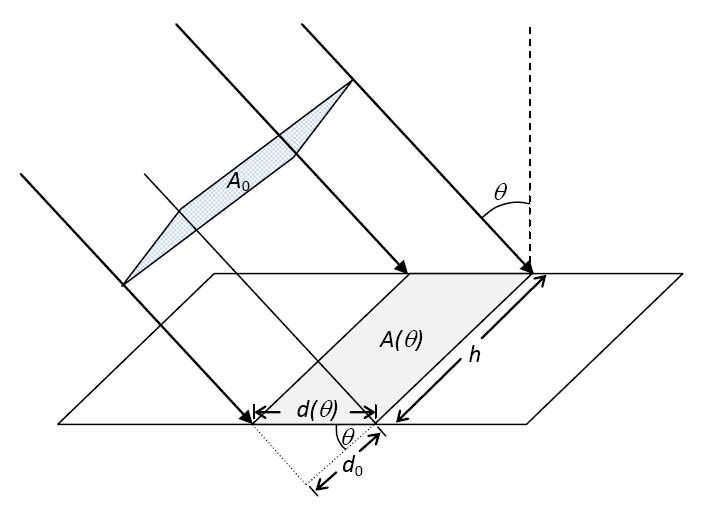
Figura 2. Irradiância sobre uma superfície. O feixe incidente tem uma secção reta
Figura 2. Irradiância sobre uma superfície.
O feixe incidente tem uma secção reta de área \(A_{0}=d_{0}h\). A área iluminada pelo feixe na superfície é \(A(\theta)=d(\theta)h\), com \(d(\theta)=d_{0}/\cos\theta\).

A irradiância é maximizada quando a superfície recetora está orientada perpendicularmente ao feixe incidente (θ = 0).

Nota: A irradiância corresponde ao módulo do vetor de Poynting da radiação eletromagnética.
 

Exitância radiante
A exitância radiante (símbolo: \(M_{e}\)) de uma superfície é a potência radiante emitida ou refletida por unidade de área:


\(M_e=\frac{d\phi_e}{dA}\)


A unidade correspondente é o W m-2.
 

Intensidade radiante
A intensidade radiante (símbolo: \(I_{e}\)) descreve a potência radiante de uma fonte emitida numa dada direção por unidade de ângulo sólido:


\(I_e=\frac{d\phi_e}{dΩ}\)


A unidade da intensidade radiante é W sr-1.

Considerando um ângulo sólido infinitesimal \(d\Omega\) centrado na fonte (Figura 3), a potência radiante da fonte no interior de \(d\Omega\) é dada por:


\(d\phi_e=I_edΩ\)



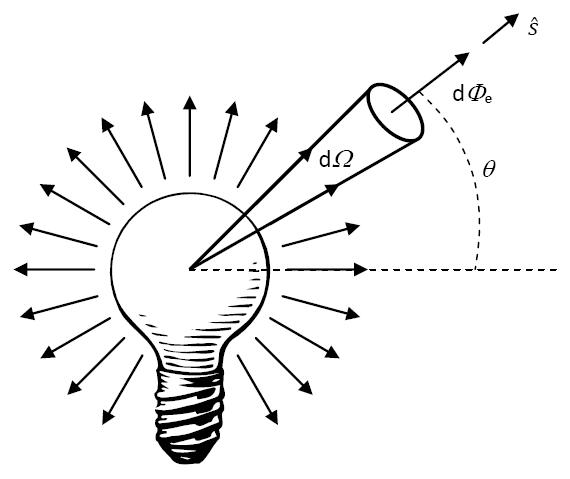
Figura 3. Geometria da definição de intensidade radiante.
Figura 3. Geometria da definição de intensidade radiante:
Φe = \(I_{e}\)\(d\Omega\) é a potência radiante no interior do ângulo sólido infinitesimal \(d\Omega\), na direção de observação definida pelo versor \(\hat{s}\), ou ângulo θ.

A potência total da fonte é calculada a partir da relação:


\(\phi_e=\int_{0}^{4\pi}I_edΩ\)


No caso de fontes de radiação anisotrópicas, a intensidade radiante depende da direção.

Nota: No campo da ótica física, a palavra intensidade é geralmente usada para designar a potência radiante por unidade de área, correspondendo à irradiância na nomenclatura da radiometria.
 

Radiância
A radiância (símbolo: \(L_{e}\)) descreve a potência radiante emitida ou refletida por unidade de ângulo sólido e por unidade de área da superfície emissora ou refletora projetada na direção do ângulo sólido. A unidade de radiância é o W m-2 sr-1.

Consideremos um elemento de superfície emissor ou refletor de radiação eletromagnética, representado pelo vetor \(\overrightarrow{dA}=dA\hat{n}\), em que \(\hat{n}\) é o versor da respetiva direção normal (Figura 4).


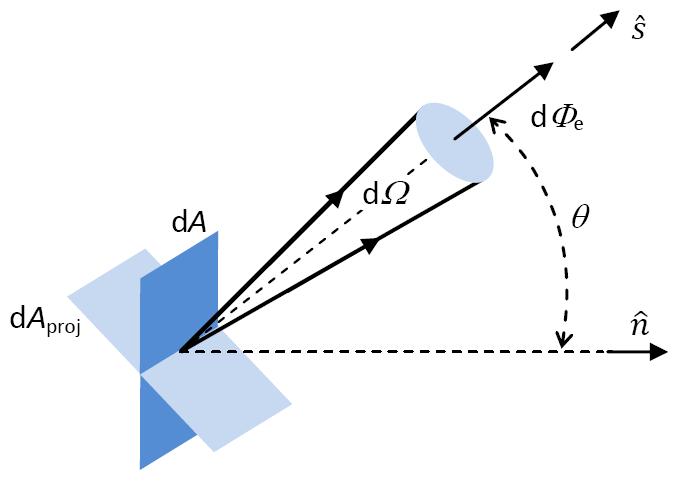
Figura 4. Geometria da definição de radiância.
Figura 4. Geometria da definição de radiância: \(d\Phi_{e}=L_{e}dA_{proj}d\Omega\) é a potência radiante no interior do ângulo sólido infinitesimal \(d\Omega\) emitida ou refletida pelo elemento de área \(\overrightarrow{dA}\),
ao qual corresponde uma área projetada \(dA_{proj}=dA\cos\theta\).

Seja \(d\Phi_{e}(\theta)\) a potência radiante proveniente deste elemento de superfície e distribuída no interior do ângulo sólido \(d\Omega\) de origem em \(\overrightarrow{dA}\) e cuja direção \(\hat{s}\) forma o ângulo θ com a normal \(\hat{n}\) do elemento de superfície. A área do elemento de superfície projetada segundo a direção \(\hat{s}\) é dada por \(dA_{proj}=dA\hat{n}\cdot\hat{s}=dAcos\theta\). Pela definição da radiância, tem-se então:



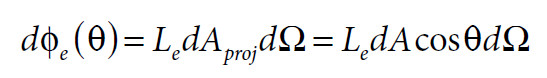
Ou seja:



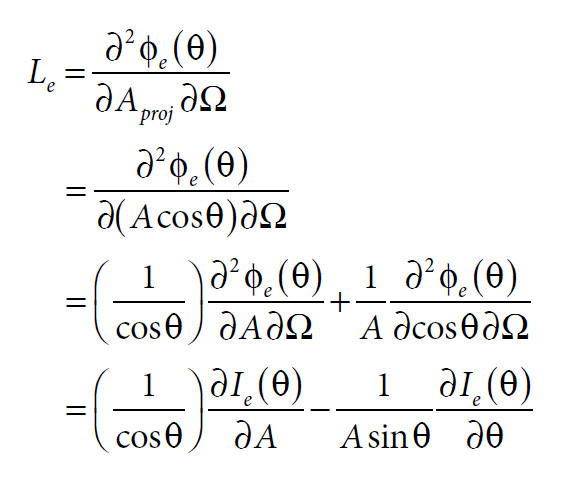
Conhecida a radiância de uma determinada superfície, pode-se obter, por integração, a correspondente exitância radiante:


\(M_e=\int_{0}^{2\pi{sr} } L_e\cosϑdΩ\)


A integração é feita sobre o ângulo sólido de 2πsr correspondente às direções de um dos lados da superfície; ϑ representa o ângulo que cada direção faz com a normal à superfície.
 

Grandezas radiométricas espetrais
As grandezas radiométricas introduzidas nas secções anteriores quantificam a radiação total sem discriminar os comprimentos de onda componentes. É também possível, e em muitos casos conveniente, usar grandezas radiométricas espetrais que têm em conta a contribuição de cada comprimento de onda, ou seja, a composição espetral da radiação.

As grandezas espetrais radiométricas representam densidades das correspondentes grandezas radiométricas por unidade de intervalo de comprimento de onda. A uma grandeza radiométrica \(X_{e}\) corresponde uma grandeza radiométrica espetral \(X_{\lambda}(\lambda)\) dada por:

\(X_\lambda(\lambda)=\frac{∂X_e}{∂\lambda}\)


A grandeza radiométrica \(X_{e}\) associada a uma grandeza espetral \(X_{\lambda}(\lambda)\) representa a área sob a curva de \(X_{\lambda}(\lambda)\) (ver Figura 5 para o caso da potência radiante), podendo ser calculada pelo integral:


\(X_e=\int_{0}^{\infty}X_\lambda(\lambda)d\lambda\)



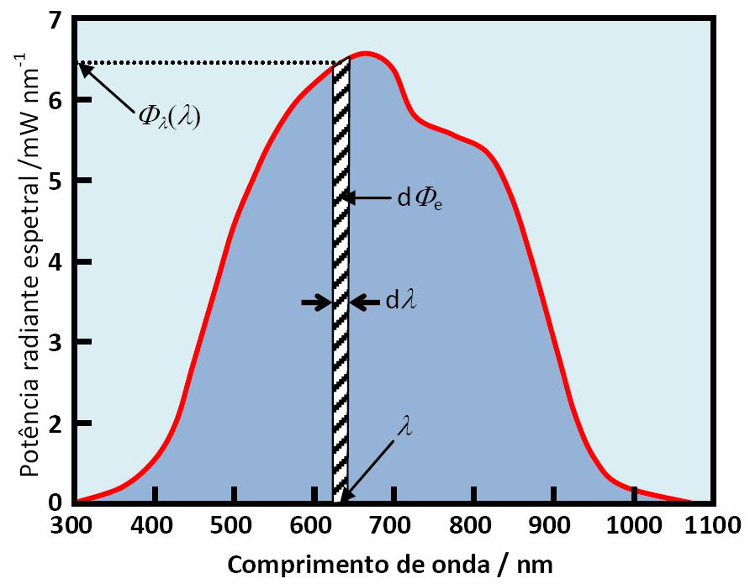
Figura 5. Relação entre potência radiante espetral.
Figura 5. Relação entre potência radiante espetral \(\Phi_{\lambda}(\lambda)\) e potência radiante Φe.
A potência radiante no intervalo de comprimento de onda entre \(\lambda\) e \(\lambda+d\lambda\) é dada pela área marcada a tracejado de valor \(\Phi_{\lambda}(\lambda)\) \(d\lambda\).