Multiplicação e divisão de números complexos
📧
- Universidade de Lisboa
Referência Carreira, A., (2015) Multiplicação e divisão de números complexos, Rev. Ciência Elem., V3(1):073
DOI http://doi.org/10.24927/rce2015.073
Palavras-chave Multiplicação; divisão; números complexos;
Resumo
Para multiplicar e dividir números complexos na forma algébrica basta ter em conta as regras habituais para operar com números reais e a relação \(i^2 = -1\).
Assim, se \(z= a + ib\) e \(w = c + id\), tem-se
- \(z\cdot w = (ac – bd) + i(ad + bc) \)
- \( \displaystyle \frac{z}{w} = \frac{a + ib}{c + id} = \frac{(a + ib)(c-id)}{(c + id)(c - id)} = \frac{(ac + bd)+i(bc – ad)}{c^{2} + d^{2}}\), se \(w\neq 0\)
A multiplicação e divisão de números complexos, na forma polar (ou trigonométrica) calcula-se para \(z= \rho(cos \alpha + i sin \alpha)\) e \(w= {\rho}’(cos \beta+ i sin \beta)\) do seguinte modo:
- \(z\cdot w = \rho {\rho}’(cos(\alpha + \beta) + isin(\alpha +\beta))\)
- \( \displaystyle \frac{z}{w}=\frac{\rho }{ {\rho }'}\) , se \(w\neq 0\)
Nota
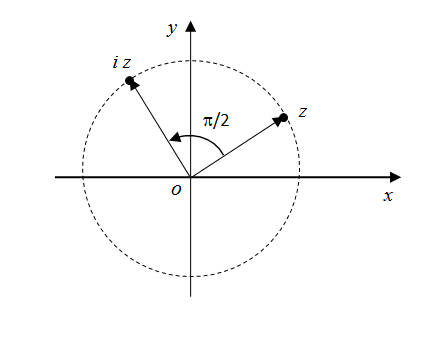
Multiplicar um número complexo não nulo pela unidade imaginária \(i\) traduz-se na rotação de \(\frac{\pi}{2}\) do vetor que o representa, como se indica na figura seguinte.
Este artigo já foi visualizado 6087 vezes.



