Uma medida de Probabilidade $\rm{P}$ é uma função de conjunto, isto é, definida em A, que a cada elemento $\rm A$ pertencente a A associa um número real que se chama Probabilidade de $\rm A$ e se representa por $\rm{P(A)}$, satisfazendo as seguintes condições ou axiomas:

1º axioma - A probabilidade de qualquer acontecimento é maior ou igual a zero

${\rm{P}}{\rm{(A) ≥ 0}}$.

2º axioma - A probabilidade do acontecimento certo $\rm S$, é 1:

${\rm{P(S) = 1}}$.

3º axioma - Dados dois acontecimentos disjuntos, a probabilidade da sua união é igual à soma das probabilidades de cada um

Se ${\rm{A}{\rm{\cap}}{\rm{B}} = \emptyset\quad\Rightarrow\quad {\rm{P(A \cup B)}} = {\rm{P(A) + P(B)}}}$

No caso de S não ser finito, a condição c) é substituída pela condição

c*) Se $\rm{A_1}$, $\rm{A_2}$, $\rm{A_3}$, ... pertencem a A então $\bigcup\limits_{ {\rm{i} } = {\rm{1}}}^\infty { { {\rm{A} }_{\rm{i} } } }$ também pertence a face="Curlz MT">A

e o 3º axioma é substituído pelo seguinte axioma:

3º axioma* - Se $\rm{A_1}$, $\rm{A_2}$, $\rm{A_3}$, ... são acontecimentos disjuntos dois a dois, então

${\rm{P(}}\bigcup\limits_{ {\rm{i} } = {\rm{1}}}^\infty { { {\rm{A} }_{\rm{i} } } }{\rm{)} } = \sum\limits_{ {\rm{i} } = {\rm{1}}}^\infty { {\rm{P(} }{ {\rm{A} }_{\rm{i}}}{\rm{)}}}$

Os axiomas anteriores são conhecidos como a axiomática de Kolmogorov.

A probabilidade frequencista, laplaciana e subjetiva, verificam a axiomática de Kolmogorov.

Como consequência da axiomática anterior, resultam as seguintes propriedades para a Probabilidade, que facilmente se ilustram com a ajuda de diagramas de Venn e se demonstram a seguir:

Propriedades da Probabilidade

1. Probabilidade do acontecimento impossível, ${\rm{P}}(\emptyset)=0$

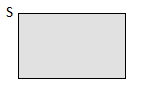
pois ${\rm{S}}= \left({\rm{S}} \cup \emptyset \right)$ e como ${\rm{S}}$ e $\emptyset$ são disjuntos, pelo 3º axioma vem	$$\rm P\left({\rm{S}} \cup \emptyset \right) = \rm P\left({\rm{S}}\right) + \rm P\left(\emptyset\right)$$
	$\quad \quad \quad \quad \quad \ = 1$.

2. Probabilidade do acontecimento complementar, ${\rm{P}}(\bar{\rm{A}})=1- {\rm{P(A)}}$

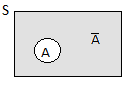
pois ${\rm{S}} = {\rm{A}} \cup \bar{\rm{A}}$ e como ${\rm{A}}$ e $\bar{\rm{A}}$ são disjuntos vem	$$\rm P\left({\rm{A}} \cup \bar{ {\rm{A} } }\right) = \rm P\left(\rm{A}\right) + \rm P\left(\bar{\rm{A}}\right)$$
	$\quad \quad \quad \quad \quad \quad \ = 1$.

3. Se ${\rm{A} }$ implica ${\rm{B} }$ (ver Operações com acontecimentos), ou seja, ${\rm{A}} \subseteq {\rm{B}}$, então ${\rm{P(A)} } \leq {\rm{P(B)} }$

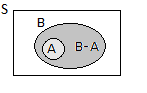
pois ${\rm{B}} = {\rm{A}} \cup {\rm{(B - A)}}$ e como ${\rm{A}}$ e ${\rm{(B-A)}}$ são disjuntos vem:

$\rm P\left({\rm{B}}\right) = \rm P\left(\rm{A}\right) + \rm P\left({\rm{(B-A)}}\right)$
$\quad \quad \quad \ \geq \rm P\left({\rm{A}}\right)$ porque $\rm P\left({\rm{(B-A)}}\right)\geq 0$ pelo 1º axioma.

4. Para qualquer acontecimento ${\rm{A}}$, tem-se $0 \leq \rm{P(A)} \leq 1$
Esta propriedade é consequência da propriedade anterior, dado que ${\rm{A}} \subseteq {\rm{S}}$.

5. Dados dois acontecimentos ${\rm{A}}$ e ${\rm{B}}$ quaisquer, tem-se ${\rm{P(A-B)}}= {\rm{P(A)-P(A \cap B)}}$

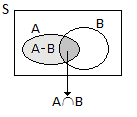
pois ${\rm{A}}= {\rm{(A-B)}}\cup {\rm{(A\cap B)}}$, com ${\rm{(A-B)}}$ e ${\rm{A \cap B}}$ disjuntos.

6. A probabilidade da união de dois acontecimentos ${\rm{A}}$ e ${\rm{B}}$ quaisquer é ${\rm{P(A \cup B)}}= {\rm{P(A)}}+{\rm{P(B)}}-{\rm{P(A\cap B)}}$

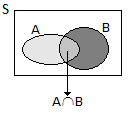
pois ${\rm{A \cup B}}= {\rm{(A-B)\cup(A\cap B)\cup(B-A)} }$, com ${\rm{(A-B)} }$, ${\rm{A\cap B}}$ e ${\rm{(B-A)} }$ disjuntos dois a dois e tendo em consideração a propriedade anterior.

Esta fórmula generaliza-se ao caso de três acontecimentos $\rm A$, $\rm B$ e $\rm C$

${\rm{P(A \cup B \cup C)}}= {\rm{P(A)}}+{\rm{P(B)}} + {\rm{P(C)}}-{\rm{P(A\cap B)}} - {\rm{P(A\cap C)}} - {\rm{P(B\cap C)}} + {\rm{P(A \cap B \cap C)}}$

ou a mais acontecimentos

Ver

• Axiomatização do conceito de probabilidade por J. Sebastião e Silva

• J. Sebastião e Silva, Compêndio de Matemática, 1º Volume, 2º Tomo

• J. Sebastião e Silva,Introdução ao Cálculo das Probabilidades: A - Frequências in Textos Didácticos Vol. 1

• J. Sebastião e Silva,Introdução ao Cálculo das Probabilidades: B - Probabilidades in Textos Didácticos Vol. 1