Cálculo aproximado. Método de exaustão

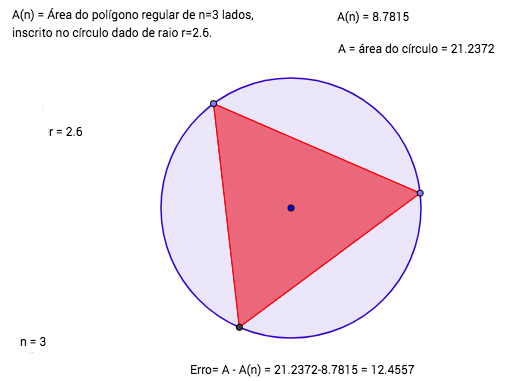
A área ${\mathcal A}$ de um círculo de raio r pode ser obtida por um processo de exaustão. Isto significa que consideramos polígonos regulares inscritos no círculo com um número n de lados, aumentando sucessivamente.

Se designarmos por ${\mathcal A}_n$ a área de um tal polígono com n lados, então ${\mathcal A}_n$ fornece uma aproximação cada vez mais fiel da área ${\mathcal A}$ do círculo, à medida que n aumenta indefinidamente. Por outras palavras

$\displaystyle\lim_{n\to\infty} {\mathcal A}_n={\mathcal A.}$

Usando a fórmula da área de polígonos regulares

${\mathcal A}_n=\displaystyle \frac{1}{2}r^2\, n\, \sin\left(\displaystyle \frac{2\pi}{n}\right)$

e o facto conhecido $\displaystyle\lim_{x\to 0}\frac{\sin x}{x}=1$, podemos calcular o limite da sucessão ${\mathcal A}_n$, obtendo

$$\displaystyle\lim_{n\to\infty} \displaystyle \frac{1}{2}r^2\, n\, \sin\left(\displaystyle \frac{2\pi}{n}\right)=\pi r^2$$

como se afirmou.