Representação polar (ou trigonométrica) de um número complexo
📧
- Universidade de Lisboa
Referência Carreira, A., (2015) Representação polar (ou trigonométrica) de um número complexo, Rev. Ciência Elem., V3(3):175
DOI http://doi.org/10.24927/rce2015.175
Palavras-chave número complexo; trigonométrica;
Resumo
Designa-se por representação polar (ou trigonométrica) ou forma polar (ou trigonométrica) de um número complexo \(z\) a sua representação na forma \(z=\rho(cos\theta+isin\theta)\), ou abreviadamente, \(z=\rho cis \theta \), em que \( \rho\) é o módulo de \(z\), \( \theta\) é um argumento de \(z\).
Geometricamente:
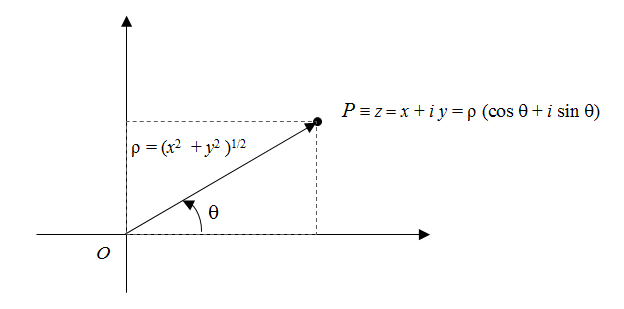
Exemplo:
Se \(z=1-i\) tem-se \(|z|=\sqrt{2}\), \(cos\theta=\displaystyle \frac{1}{\sqrt{2}} \) e \(sin\theta=\displaystyle \frac{-1}{\sqrt{2}}\).
Assim, tomando o argumento principal, \( z=\sqrt{2}\left(cos\left(\displaystyle -\frac{\pi}{4}\right)+isin\left(\displaystyle -\frac{\pi}{4}\right)\right) \) e, tomando o argumento positivo mínimo, \( z=\sqrt{2}\left(cos\left(\displaystyle \frac{7\pi}{4}\right)+isin\left(\displaystyle\frac{7\pi}{4}\right)\right)\).
Ver
Este artigo já foi visualizado 7312 vezes.



