Alguns processos nucleares são responsáveis pelo brilho das estrelas mas só em 1920 é que os primeiros processos nucleares foram formalmente estudados, pelo astrónomo Sir Arthur Eddington (1882 – 1944), que propôs modelos estelares que envolviam fusões nucleares. Contudo, só nos anos 30 é que a fusão nuclear foi verificada experimentalmente. Em 1932 a fusão de isótopos de hidrogénio foi conseguida em laboratório e em 1939 o físico nuclear Hans Bethe (1906 – 2005) descreveu os processos de fusão nuclear que ocorrem nas estrelas (nucleossíntese estelar). Em 1938, a fissão nuclear foi, pela primeira vez, observada por Otto Hahn (1879 – 1968) e Fritz Strassmann (1902 – 1980) que dispararam neutrões contra núcleos de urânio com o objetivo de produzir um núcleo mais pesado.¹ Contudo, verificaram a formação de elementos com cerca de metade da massa do urânio. Este facto intrigou os investigadores visto que estava a ser observado um núcleo a partir-se em dois.

Consideremos uma partícula (P) em movimento a embater numa partícula alvo (T) em repouso:

P (partícula projetada) + T (partícula alvo) \(\longrightarrow\) x (partícula emitida) + R (núcleo residual)

Para este tipo de reações nucleares, desprezando a energia de ligação dos eletrões, podemos estabelecer o seguinte balanço energético

\(m_Pc^2+E_c(P)+m_Tc^2=m_Rc^2+E_c(R)+m_xc^2+E_c(x) \qquad \qquad (1)\)

em que E_c(i) e m_i são, respetivamente, a energia cinética e a massa da partícula i e c é a velocidade da luz. (Note-se que o produto m_ic² também pode ser designado “energia de repouso” de uma partícula. Repare-se, também, que, como se partiu do princípio de que a partícula T estaria em repouso, esta não possui energia cinética.)

Desta forma pode ser definido o valor Q, que corresponde à diferença das massas de repouso dos reagentes pelos produtos

\(Q=[m_P+m_T-(m_R+m_x)]c^2=E_c(x)+E_c(R)-E_c(P) \qquad \qquad (2)\)

Com esta definição, é possível verificar que, se Q for positivo, a reação nuclear será exoenergética e, consequentemente, se Q for negativo, a reação será endoenergética – a convenção de sinais é oposta da utilizada na variação de entalpia, ΔH, das reações químicas. Assim, com este balanço energético verifica-se que uma das condições necessárias, mais não suficiente, para que ocorra uma reação nuclear é

\(Q+E_c(P)>0 \qquad \qquad (3)\)

dado que, para que a reação ocorra, será necessário que as partículas formadas possuam alguma energia cinética.²

Para avaliar se uma reação nuclear é endoenergética ou exoenergética é necessário ter em consideração que, no núcleo, as forças nucleares fortes (atrativas e que mantêm o núcleo coeso) devem estar minimamente equilibradas com as forças electroestáticas (repulsivas que tendem a afastar os protões entre si). As forças nucleares são bastante mais fortes que as forças eletromagnéticas para distâncias até pouco mais de 2 vezes o diâmetro do protão. Para lá dessa distância, as forças eletromagnéticas são superiores às forças nucleares.

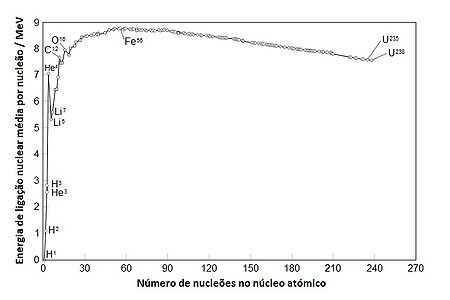
Assim, com o aumento do número atómico, maior será a estabilidade do núcleo e, consequentemente, a energia de ligação do núcleo. No entanto isto só acontece até ao limite em que as forças electroestáticas superam as forças nucleares (um pouco mais de 2 vezes o diâmetro do protão). Esse limite é atingido para o elemento químico ferro, Fe; após esse elemento, o aumento do número de nucleões resulta numa diminuição da energia de coesão nuclear – ver figura 1. Isto acontece porque, a partir do ferro, as forças electroestáticas, de natureza repulsiva, começam a superar as forças nucleares, instabilizando o núcleo atómico.

É por este motivo que, até ao elemento químico ferro, a fusão nuclear é uma reação exoenergética e para lá desse elemento é a fissão nuclear que é exoenergética. Em ambos os casos, o facto de a reação ser exoenergética depreende-se com a necessidade de estabilização do núcleo. Por esta razão é que, para obter energia, é necessário fundir núcleos leves ou cindir núcleos pesados.

Existem muitos tipos de reações nucleares: fusão nuclear, fissão nuclear, espalação nuclear, decaimento por emissão de partículas α, decaimento β ⁻ , entre outros, como se exemplifica:

\({}_2^3 He + {}_2^3 He \longrightarrow {}_2^4 He + 2\ {}_1^1 H\)            Fusão Nuclear

\({}_{92}^{235} U + {}_0^1 n \longrightarrow {}_{56}^{142} Ba + {}_{36}^{91} Kr + 3\ {}_0^1 n\)            Fissão Nuclear

\({}_{0}^{1} n + {}_{7}^{14} N \longrightarrow {}_{1}^{1} p + {}_{6}^{14} C\)            Espalação Nuclear

\({}_{92}^{238} U \longrightarrow {}_{90}^{234} Th + {}_{2}^{4} He\)            Decaimento \({\displaystyle \alpha}\)

\({}_{55}^{137} Cs \longrightarrow {}_{56}^{137} Ba + e^- + \bar{\nu}_e\)            Decaimento β ⁻

A escrita de equações que traduzem reações nucleares obedece a duas regras específicas⁴:

• Regra Z – A soma dos números atómicos, Z, das partículas reagentes é igual à soma dos números atómicos dos produtos de reação;
• Regra A – A soma dos números de massa, A, das partículas reagentes é igual à soma dos números de massa dos produtos da reação.

Note-se que a energia envolvida nestes processos é expressa em MeV/átomo em vez de kJ/mol, o que evidencia a enorme diferença entre as ordens de grandeza das energias envolvidas nas reações químicas e nas nucleares.⁴ Por exemplo, a combustão do gás propano debita 2220 J por cada mole de gás (3,686 x 10^-21 J/molécula de propano) que reage enquanto a referida reação de fissão nuclear do urânio debita 19,3 x 10¹² J por cada mole de átomos de urânio-235 (3,20 x 10^-11 J/átomo = 200 MeV/átomo).^‡

As reações nucleares têm variadas aplicações, dependendo do tipo a que pertencem. Permitem, por exemplo, o abastecimento de redes de energia elétrica, a datação de artefactos históricos e, infelizmente, permitiram a criação do material bélico mais destrutivo do planeta.

‡ Como 1 eV = 1,6022 x 10^-19 J, 1 MeV/átomo corresponde a 9,65 x 10⁷ kJ/mol.⁵