Série de Balmer
📧
- Faculdade de Ciências da Universidade do Porto
Referência Lima, L.S., (2015) Série de Balmer, Rev. Ciência Elem., V3(3):192
DOI http://doi.org/10.24927/rce2015.192
Palavras-chave Balmer; eletrónicas; átomo de hidrogénio; radiação; ultra-violeta (UV);
Resumo
A série de Balmer corresponde ao conjunto de transições eletrónicas num átomo de hidrogénio de estados excitados (n \(\geq\) 3) para o nível n = 2 responsáveis pela emissão de radiação na zona do visível e do ultra-violeta (UV) próximo.
A figura 1 representa o espectro de emissão de riscas do átomo de hidrogénio na zona do visível e ultravioleta. As quatro primeiras riscas a contar da direita para a esquerda correspondem às transições de menor energia e situam-se na zona do visível. As riscas marcadas a cinzento já estão situadas na zona do UV próximo, dado o seu comprimento de onda (λ) ser inferior a 400 nm. Cada transição é designada de forma sequencial por uma letra do alfabeto grego. Assim, a primeira transição (n = 3 \(\rightarrow\) n = 2) é designada por H-\(\alpha\), a segunda transição (n = 4 \(\rightarrow\) n = 2) é designada por H-\(\beta\) e assim sucessivamente.
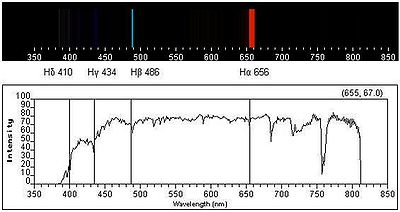
As características das transições da série de Balmer estão compiladas na tabela seguinte:
| Transição | 3\(\rightarrow\)2 | 4 \(\rightarrow\)2 | 5 \(\rightarrow\)2 | 6 \(\rightarrow\)2 | 7 \(\rightarrow\)2 | 8 \(\rightarrow\)2 | 9 \(\rightarrow\)2 | \(\infty\) \(\rightarrow\)2 |
|---|---|---|---|---|---|---|---|---|
| Nome |
H-\(\alpha)\
|
H-\(\beta\)
|
H-\(\gamma)\
|
H-\(\delta)\
|
H-\(\epsilon\)
|
H-\(\zeta\)
|
H-\(\eta\)
|
|
| \(\lambda\) /nm[1] |
656,3
|
486,1
|
434,1
|
410,2
|
397,0
|
388,9
|
383,5
|
364,6
|
| Energia / kJ\(\cdot\)mol-1 |
182,3
|
246,1
|
275,6
|
291,6
|
301,3
|
307,6
|
311,9
|
328,1
|
| Cor |
Vermelha
|
Azul-esverdeada
|
Violeta
|
Violeta
|
(UV)
|
(UV)
|
(UV)
|
(UV)
|
Esta série foi assim designada em homenagem ao matemático suíço Johann Balmer, pois foi ele, em 1885, o primeiro a desenvolver uma fórmula empírica que permitia prever o comprimento de onda de qualquer transição eletrónica num átomo de hidrogénio de um estado excitado para o nível n = 2. Três anos mais tarde, o físico sueco Johannes Rydberg generalizou a fórmula de Balmer de modo a poder prever-se o comprimento de onda da radiação emitida em qualquer transição eletrónica entre dois níveis no átomo de hidrogénio:
\(\frac{1}{\lambda}=R \left ( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right ) \qquad \mbox{com } n_1 < n_2 (n=1,2,3,...) \qquad \qquad \qquad\qquad \qquad (1)\)
Esta expressão é hoje conhecida como fórmula de Rydberg, e inclui a fórmula de Balmer como caso particular (n2 > 2 e n1 = 2).
Nesta equação, n1 e n2 representam os níveis atómicos correspondentes à transição eletrónica n2 \(\rightarrow\) n1, R representa a constante de Rydberg, R = 1,097 373 156 852 5 (73) \(\times\) 107 m-1. No caso da série de Balmer, n1 = 2.
A série de Balmer tem uma grande aplicação na área da astronomia, pois está presente nos espectros de emissão de inúmeros corpos estelares (dada a elevada abundância de hidrogénio no Universo), o que é utilizado para a classificação das estrelas em termos da temperatura da sua superfície com base na intensidade das linhas do espectro de emissão. É, ainda utilizada na deteção de objetos estelares como grupos de galáxias, grupos de estrelas, estrelas de neutrões ou buracos negros e, também, na determinação de distâncias entre galáxias.
Este artigo já foi visualizado 10643 vezes.



