O Geopark caracteriza-se por amplas áreas aplanadas (Meseta) com uma evolução por etapas durante o Mesocenozóico, ou seja, nos últimos 250 milhões de anos, sobre um soco muito antigo, com rochas de origem sedimentar datadas do Neoproterozóico (Grupo das Beiras, com cerca de 600 milhões de anos). Da superfície da Meseta irrompem numerosos relevos residuais, dos quais se salientam as cristas quartzíticas ordovícicas e os inselberge ou montes- ilha graníticos (Monsanto), bem como as bacias intramontanhosas com preenchimentos sedimentares relacionados com a Orogenia Alpina. Destaque para as redes hidrográficas profundamente entalhadas durante as crises climáticas do Plistocénico e induzidas por importantes fenómenos de tectónica recente que recortaram a paisagem em vários blocos (grabens e horsts) e dão origem a algumas das águas termais existentes no território.

(grabens e horsts) e dão origem a algumas das águas termais existentes no território. Pretende-se com este trabalho atravessar 600 milhões de anos e um conjunto de acontecimentos que se interligam e que compõem a história geológica do Geopark Naturtejo. Desta vez, iremos descobrir o que nos conta uma das rochas mais importantes do geoparque, responsável pelos elementos mais significativos do seu património geológico e da sua paisagem: os quartzitos.

Parque Icnológico de Penha Garcia

O sítio paleontológico do Parque Icnológico de Penha Garcia, um dos mais visitados geomonumentos do Geopark Naturtejo, é conhecido e estudado desde 1883, sobretudo no que diz respeito ao conteúdo paleontológico da Formação do Quartzito Armoricano, sendo que são especificamente as evidências de actividade paleobiológica que lhe dão reconhecimento, estando expostos ao longo do vale, como quadros numa impressionante galeria de arte.

São conhecidas 36 formas de comportamento animal que tipificam esta formação com distribuição nas áreas costeiras que circundavam o antigo continente Gondwana. Esta jazida é considerada como referência internacional para o grupo Cruziana rugosa pela diversidade de comportamentos determinados, qualidade de preservação, dimensões (variando entre mm e as maiores Cruziana que se conhecem no registo paleontológico mundial), assim como a muito rara atribuição a um produtor (trilobite Asaphida) que coocorre nas mesmas rochas. A interpretação de Cruziana como escavações de alimentação atribuíveis a trilobites foi desenvolvida por Roland Goldring (1985) com base em recolhas feitas também em Penha Garcia, nos finais da década de setenta. São ainda reconhecidos comportamentos de crustáceos filocarídeos, de bivalves, de anémonas e de vermes (incluindo poliquetas sésseis e errantes). Devese realçar a ocorrência de uma pista de locomoção do tipo Merostomichnites atribuída a filocarídeos. Apenas se conhecem duas ocorrências em Portugal e esta é a única observável. Tratam-se dos vestígios mais antigos deste grupo de artrópodes encontrados em Portugal.

O património paleontológico de Penha Garcia continua a revelar valores significativos à medida que são feitas novas descobertas pelos investigadores que ali trabalham, sustentados pela nobre herança deixada por grandes paleontólogos como Nery Delgado, Roland Goldring e Adolf Seilacher^{3, 5, 6, 11}.

O Parque Icnológico de Penha Garcia e o seu diversificado património geológico são percorridos pela Rota dos Fósseis, um percurso pedestre temático que atravessa a garganta rochosa do rio Ponsul e inclui também a Casa dos Fósseis, um espaço que alberga espécimes de fósseis, rochas e minerais locais e interpreta os processos de fossilização e os comportamentos deixados pelos organismos que aí viveram.

Este impressionante registo fóssil do Ordovícico, com uma idade compreendida entre os 479,1 e os 443,8 milhões de anos (Ma) não é o mais antigo do Geopark Naturtejo. Existem rochas do Ediacariano Superior, com fósseis dos mais antigos conhecidos em Portugal, datados de há cerca de 580 a 540 milhões de anos, em Salvaterra do Extremo e Monfortinho, que revelam a existência de oceanos cobertos de gelo num período da história da vida em que existiam quase somente formas unicelulares. Tratam-se de microfósseis planctónicos, como acritarcas¹².

Serra do Muradal

A oeste de Penha Garcia situa-se o relevo quartzítico do Muradal, do tipo “Apalachiano”. Esta montanha ergue-se desafiante, quase meio quilómetro acima da Superfície de Castelo Branco que se estende, monótona e ocasionalmente retalhada pela incisão fluvial, até aos pés da Cardilheira Central¹⁰. O icnofóssíl do tipo Daedalus é uma das mais intrigantes formas de comportamento que se encontram nas rochas quartzíticas desta montanha (FIGURA 3). Múltiplas marcas que lembram uma qualquer escrita ancestral indecifrável comprovam a existência de vida abundante quando, outrora, estas rochas dispostas em camadas eram sedimentos de um fundo marinho, do primitivo oceano Rheic, onde a vida proliferou e evoluiu. Um misterioso animal escavou sistematicamente a partir do fundo arenoso onde viveu, construindo sucessivas galerias verticais em forma de J dispostas de modo centrípeto, constituindo a três dimensões um cone, com o propósito de se alimentar do único recurso nutritivo em areias de quartzo lavadas pelo mar – películas de bactérias que envolviam os grãos.

Este estranho e complexo modo de viver viria a extinguir-se para sempre, conjuntamente com o animal que o produziu, há cerca de 430 Ma. Estes são testemunhos de uma vasta planície costeira que se estendia por quilómetros, cuja dinâmica pode ser testemunhada na Serra do Muradal. Ali se podem observar as evidências da abertura de um oceano, o seu fecho e a consequente deformação das rochas (FIGURA 4) sob enormes pressões, durante a formação do supercontinente Pangeia, e a formação progressiva da crista Apalachiana do Muradal. Esta crista é atravessada pelo percurso pedestre da Grande Rota Muradal- -Pangeia, integrado no Trilho Internacional dos Apalaches que pretende ligar territórios norte-americanos, europeus e norte-africanos, outrora unidos na Pangeia, e que foram afastados pela abertura do oceano Atlântico. Este percurso temático evoca o supercontinente Pangeia, que existiu até há 200 Ma, com passagem por locais de interesse geológico, geomorfológico, paleontológico, biológico, histórico e cultural, incluindo uma Escola de Escalada e uma Via Ferrata – Caminho sobre o Oceano Ordovícico.

Vale Mourão e as Portas de Almourão

As formações sedimentares, que ocorreram nos fundos marinhos há cerca de 500 Ma, surgem agora nos cumes das serras do Muradal, Penha Garcia e Talhadas. Estes materiais foram enrugados e elevados por forças compressivas derivadas da gigantesca colisão continental que originou a formação da Pangeia. A magnitude desta colisão continental pode ser testemunhada em Vale Mourão⁴, onde a consequente elevação da grande cordilheira montanhosa Varisca está bem patente na paisagem, com camadas verticalizadas e rochas dobradas e redobradas, em estruturas sinformas e antiformas dignas de respeito (FIGURA 5), como é o caso da Dobra Albarda. Neste contexto, o imponente geomonumento das Portas de Almourão desvenda uma impressionante garganta epigénica escavada pelo rio Ocreza nos últimos 2 Ma, tendo dado origem a um desfiladeiro com quase 400 m de profundidade (FIGURA 6). O rio aproveitou uma zona de fraqueza estrutural, pela existência de falhas, para entalhar o leito através da Serra das Talhadas. A geodinâmica e a dinâmica fluvial das Portas de Almourão fizeram com que as aldeias localizadas a jusante da garganta, Foz do Cobrão e Sobral Fernando, tenham sido locais com tradição para a exploração de ouro, desde o período romano até meados do século XX. Sobral Fernando é uma aldeia típica construída literalmente em cima de uma mina de ouro, uma conheira que aí ainda se pode visitar.

A este propósito, o percurso pedestre “Rota das Conheiras” percorre os vestígios destas antigas conheiras e a actividade “Há Ouro na Foz”, tradição recuperada pelo geoparque, permite experimentar o garimpo de ouro nas margens do Ocreza, utilizando técnicas milenares. Em Vale Mourão são vários os miradouros temáticos sobre o geomonumento das Portas de Almourão e sobre a flora e fauna da crista quartzítica que permitem uma leitura clara sobre a incisão fluvial e os ecossistemas rupícolas. A interpretação dos processos de deformação pode ser feita através de percursos pedestres guiados que cruzam a garganta e acompanham a deformação bem patente nas rochas, como “Os Segredos de Vale Mourão”, “Viagem pelos Ossos da Terra” e “Caminho do Xisto -Voo do Grifo”.

Vale do Tejo e as Portas de Ródão

A Serra das Talhadas, tal como a Serra de Penha Garcia ou a Serra do Muradal, exibe rochas quartzíticas coesas e duras que eram originalmente areias móveis em fundos marinhos, como podemos comprovar pela existência de marcas de ondulação (ripple marks) comparáveis com aquelas que encontramos hoje nas praias e que nos indicam que este mar tinha aqui poucos metros de profundidade. Os quartzitos são rochas neste contexto particularmente resistentes à erosão, formando relevos residuais que sobressaem na paisagem quando as rochas xistentas menos resistentes que os envolvem são erodidas. No Geopark Naturtejo estes relevos tão característicos, que constituem verdadeiras muralhas naturais, compõem os relevos apalachianos, como na serra de Penha Garcia, na serra do Muradal, na serra de Monforte da Beira ou na serra das Talhadas.

É precisamente na serra das Talhadas que se localizam as Portas de Ródão, em pleno curso do rio Tejo, um dos mais importantes rios da Península Ibérica, que ali corre entrincheirado, submisso, entre gigantes quartzíticos (FIGURA 7). O Rio Tejo aproveitou a intersecção de quatro acidentes tectónicos gerando um vale encaixado nas serras de Talhadas e Perdigão, que atinge 45 m na largura mínima, entre escarpas quartzíticas com cerca de 200 m de altura. A incisão fluvial terá avançado a uma velocidade média de 10 cm por 1000 anos¹, tendo começado há cerca de 2,6 Ma, como se pode observar pelas etapas sucessivas de encaixe materializadas nos terraços fluviais².

Com base nas características geológicas e geomorfológicas, toda a área do Monumento Natural das Portas de Ródão encerra uma importante biodiversidade e um rico património arqueológico, marcado pela excepcionalidade do Complexo de Arte Rupestre do Tejo e também associado à ocupação dos terraços fluviais. Por exemplo, no Paleolítico Inferior, que remonta há mais de 150 000 anos, as cascalheiras dos terraços ofereceram ao ser humano matéria-prima para a construção de inúmeras ferramentas, que estão ainda hoje bem preservados.

Um passeio de barco pelas águas tranquilas do rio Tejo apresenta de vários prismas, científicos aos puramente estéticos, o Monumento Natural, permitindo cruzar as Portas do Ródão, que podem também ser observadas de vários miradouros temáticos dedicados ao património geológico e à biodiversidade. Percursos pedestres, como a Rota das Invasões, Trilhos do Conhal ou o Caminho das Virtudes, oferecem perspectivas magníficas sobre as Portas de Ródão e sobre as cristas quartzíticas paralelas das serras das Talhadas e do Perdigão. Destaque ainda para o percurso “Geologia e Arqueologia Urbanas” que proporciona uma abordagem integradora entre os vestígios arqueológicos e o substrato geológico.

Árvores Fósseis

Precisamente num destes terraços do Tejo, no Monte do Pinhal (designado T1)2 foram encontrados os Troncos Fósseis de Vila Velha de Ródão (veja-se Neto de Carvalho & Rodrigues 2008)(FIGURA 8). O terraço fluvial do Monte Pinhal é o mais antigo e aquele que se dispõe a altitude mais elevada, à cota dos 180m e a 120m do leito actual do Tejo, tendo os troncos sido postos a descoberto entre os amontoados de seixos rolados de uma conheira, durante a exploração aurífera levada a cabo possivelmente durante o domínio Romano. Este terraço, datado de há cerca de 1,6 Ma², ravina depósitos cenozóicos anteriores, pelo que os troncos terão sido remobilizados das sequências arcósicas mais antigas por acção fluvial e depositados a jusante.

O forte desgaste dos fósseis, as incisões de choque provocadas por seixos assim como a ampliação das fracturas pré-existentes que os seccionam, mostram que os troncos assentaram, em parte, num leito fluvial de elevada energia, cascalhento, posteriormente à sua fossilização. Assim, os troncos fósseis serão mais antigos do que os depósitos plistocénicos do Tejo, possuindo entre 15 e 5 Ma. Estes troncos e outros conhecidos partilham as características de uma mesma árvore atribuída a Annonoxylon teixeirae, cuja representante actual mais conhecida são as xilópias, do grupo das Anonáceas, indicando que o clima nesta região terá sido tropical, quente e húmido, mas com estações contrastantes.

Cascata da Fraga da Água d’Alta e os fósseis vivos da antiga Laurissilva

Estes troncos fossilizados são os últimos testemunhos de uma floresta que já não existe na região, assim como os vestígios actuais de Laurissilva, recentemente encontrados na Fraga da Água d’Alta, que actualmente apenas persistem em alguns locais da Macaronésia e em alguns refúgios da Europa continental, com destaque para o azereiro (Prunus lusitanica), o folhado (Viburnum tinus), o amieiro negro (Frangula alnus L.) ou o Omphalodes nitida, um endemismo Ibérico. Estes vestígios de Laurissilva são autênticos fósseis vivos, representando florestas antigas que remontam ao período Terciário.

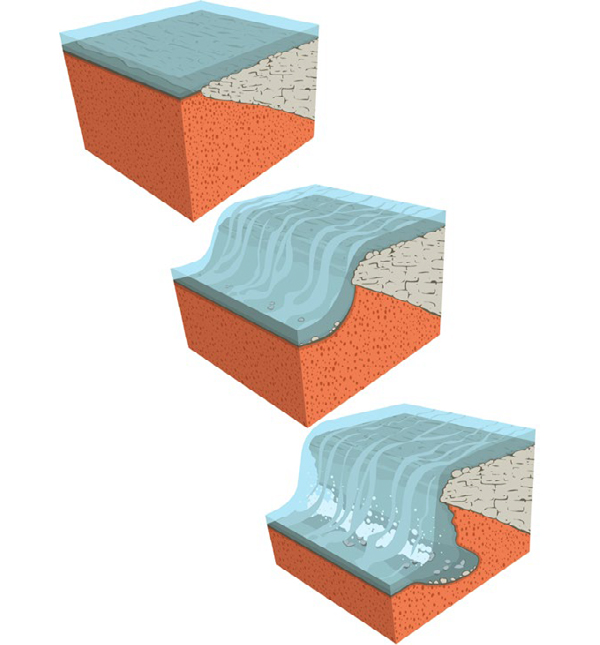
Deste paraíso agora encontrado destaca-se também as cascatas da Fraga da Água d’Alta, onde se observa a evolução do perfil do ribeiro que, nas condições climáticas actuais, vai regularizando os três relevos estruturais pela erosão e tenta alcançar o seu perfil de equilíbrio, um processo erosivo que se assemelha ao que terá levado, na sua fase inicial, à formação das gargantas das Portas de Almourão ou Portas de Ródão (FIGURA 10 e FIGURA 11). As bancadas métricas de quartzitos alternam com bancadas mais finas de quartzitos e xistos, essas menos resistentes à erosão fluvial, ocorrendo um encaixe diferencial da linha de água. O Vale das Cardosas é atravessado pela GeoRota do Orvalho, um percurso pedestre que aborda a riqueza da geodiversidade, da biodiversidade e do património cultural, deste troço da Serra do Muradal.

Este património geológico excepcional, de origem quartzítica, que pauta o Geopark Naturtejo tem sido alvo de estratégias de geoconservação e divulgação para um público diversificado: habitantes, turistas, geoturistas, professores, estudantes e grupos heterogéneos, com o desenvolvimento de ferramentas apropriadas, estratégias específicas e guias especializados⁹. A interpretação da história geológica do Geopark Naturtejo, dos materiais e dos processos envolvidos, é fundamental na conservação dos valores da Geodiversidade, sensibilizando para a sua importância e vulnerabilidade. Por milhões de anos os duros quartzitos construíram a paisagem do Geopark Naturtejo. Mas mesmo estas rochas mais duras voltam e voltarão à sua condição original de areias de praia…

Neste artigo, é apresentada a análise genérica, mas detalhada, do movimento do pêndulo simples, ignorando, primeiro, a rotação da Terra, para, depois, se estudar o pêndulo de Foucault.

Descrição mecânica

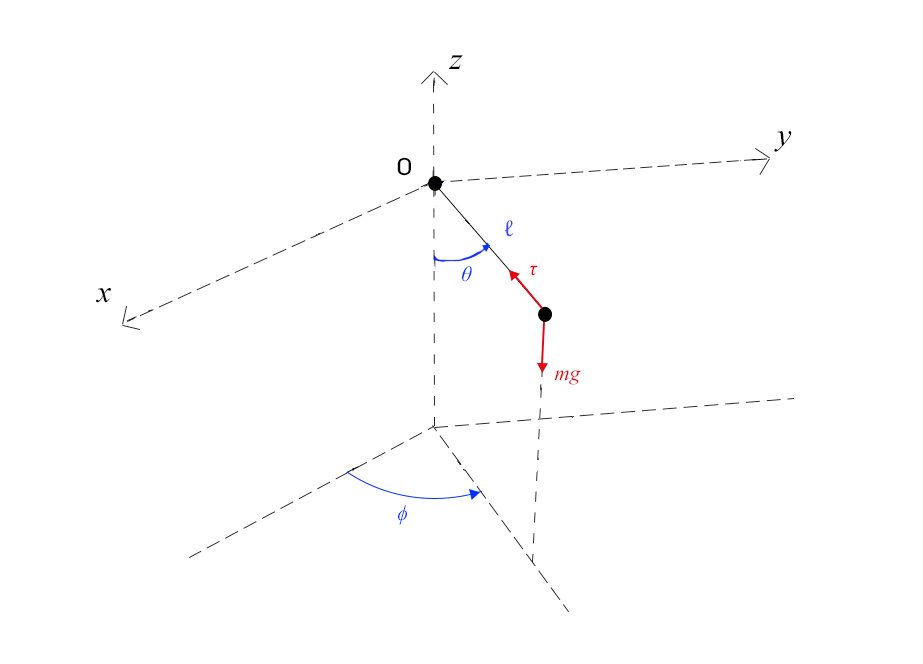
A FIGURA 2 mostra a caracterização dos dois graus de liberdade do pêndulo e as forças que sobre ele atuam. Consideramos um sistema tri-rectangular de eixos \(Oxyz\) com origem no ponto de suspensão, eixo \(z\) vertical. Este eixo e o fio, de comprimento ℓ, definem o plano do pêndulo e permitem a sua caracterização mecânica através dos ângulos \(\theta\) que o fio faz com a vertical e \(\phi\) que o plano do pêndulo faz com um outro plano vertical fixo, contendo a origem (na figura, o plano \(x\),\(z\)). Indicamos, também, as forças que se fazem sentir sobre a massa \(m\) presa na extremidade livre do fio: o seu peso, \(mg\), vertical e a tensão \(τ\) exercida pelo fio. Daqui resulta uma imediata e importante consequência: o fio pode puxar a massa, mas não a pode empurrar, pelo que:

\(τ ≥ 0\)            (1)

Se esta condição não se verificar, o fio deixa de estar esticado e o movimento tem que passar a incluir a distância à origem como uma nova variável dinâmica, i.e., o sistema terá três graus de liberdade.

Posto isto, a lei fundamental da dinâmica escreve-se:

\(m\vec{a}=m\vec{g}+\vec{τ}\)            (2)

Note-se que a energia mecânica conserva-se: o peso deriva de um potencial e a tensão não realiza trabalho, com o fio esticado, e desaparece se ele deixar de estar esticado. Há três incógnitas no problema: os dois ângulos \(\theta\) e \(\phi\) e a tensão τ. É conveniente usarmos uma base local definida por três versares ortonormados (FIGURA 3):

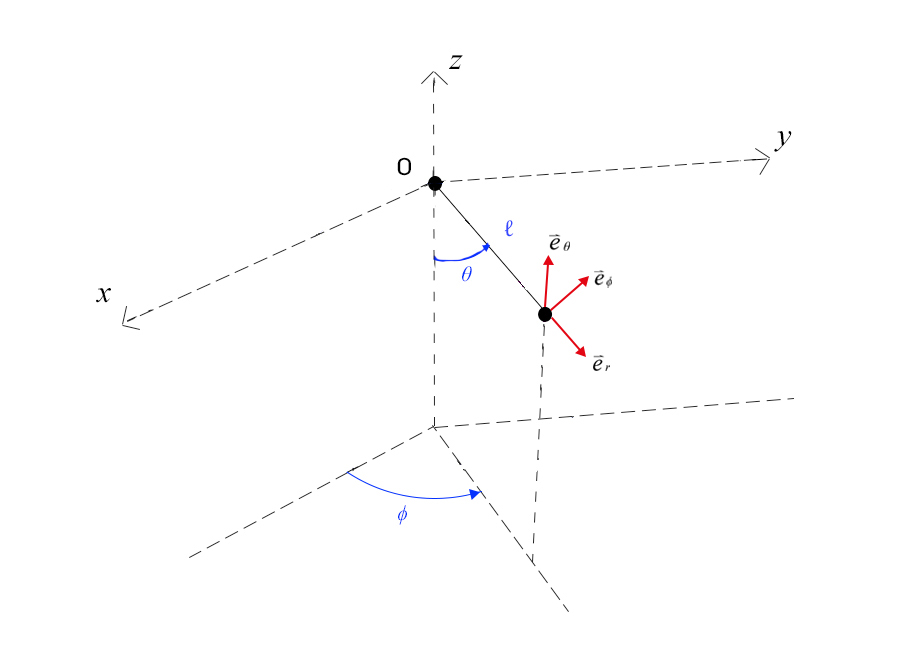
\(\vec{e}_{r}\): aponta da origem para a massa

\(\vec{e}_{\phi}\): perpendicular ao plano do pêndulo, com o sentido em que \(\phi\) cresce

\(\vec{e}_{\theta}\): no plano do pêndulo, perpendicular ao eixo, com o sentido em que \(\theta\) cresce

O conjunto (\(\vec{e}_{r}\), \(\vec{e}_{\phi}\), \(\vec{e}_{\theta}\)), nesta ordem, forma um referencial

direto:

\(\vec{e}_{r}\times \vec{e}_{\phi}=\vec{e}_{\theta}\)            (3)

Da figura, obtém-se facilmente as componentes cartesianas destes versares:

\(\vec{e}_{r} = (sen \ \theta \ cos\ \phi, sen \ \theta \ sen \ \phi, - cos\ \theta)\)

\(\vec{e}_{\theta} = (cos \ \theta \ cos\ \phi, cos\ \theta \ sen\ \phi, sen\ \theta) =\frac{\partial \vec{e}_r}{\partial \theta}\)

\(\vec{e}_{\phi} = (-sen\ \phi, cos\ \phi, 0)\)

Posto isto, partindo do vector de posição da massa:

\(\vec{r}=ℓ\vec{e}_{r}\)            (4)

obtemos a expressão da velocidade derivando em ordem ao tempo:

\(\vec{v}=\ell\frac{d \vec{e}_r}{dt}=\ell\left[\frac{\partial \vec{e}_r}{\partial\theta }\theta^.+\frac{\partial \vec{e}_r}{\partial\phi }\phi^.\right]=\ell\left[\theta^.\vec{e}_\theta+\phi^.\ sen\ \theta \ \vec{e}_\phi\right]\)            (5)

e, com um pouco mais de trabalho, a sua aceleração:

\(\vec{a}=\ell\left[-(\dot{\theta}^{2}+\dot{\phi}^{2}sen^2\theta) \vec{e}_r+(\ddot{\theta}-\dot{\phi}^{2}sen \ \theta \ cos \ \theta) \ \vec{e}_\theta + (2 \ \dot{\phi}\dot{\theta} \ cos \ \theta \ + \ \ddot{\phi} \ sen \ \theta)\vec{e}_\phi\right]\)            (6)

Notando que \(\vec{\tau}=-\tau\vec{e}_r\) e \(\vec{g}=-g \ \vec{e}_z=-g \ (sen \ \theta \ \vec{e}_\theta- cos \ \theta \ \vec{e}_r)\), podemos reescrever as eqs. (2) sob a forma das três seguintes equações para as suas componentes na base local:

\(-m\ \ell \left[\dot{\theta}^2+\dot{\phi}^2 \ sen^2 \theta\right]=-\tau + mg\ cos\ \theta\)             (7a)

\(m\ \ell \left[\ddot{\theta}+\dot{\phi}^2 \ sen\ \theta \ cos\ \theta\right]=-mg \ sen \ \theta\)            (7b)

\(m\ \ell \left[2\ \dot{\phi} \dot{\theta} \ cos\ \theta \ + \ddot{\phi} \ sen \ \theta \right]=0\)            (7c)

Esta última equação reescreve-se como:

\(\frac{1}{sen\ \theta}\frac{d}{dt}(\dot{\phi} \ sen^2 \ \theta)=0\)

Encontramos, assim, um integral primeiro:

\(\dot{\phi }sen^{2}\theta \)= constante            (8)

Qual a origem física deste resultado? Observando a FIGURA 1, vemos que, se se considerar o momento das forças com pólo na origem, apenas o peso contribui, sendo, pois nula, a sua projeção vertical. Então, pelo teorema dos momentos cinéticas, deverá ser constante a componente \(L_z\) . Ora:

\(\vec{L}=\vec{r} \ \times \ (m \ \vec{v})= m \ell^2\left[- \dot{\theta} \ \vec{e}_\phi \ + \dot{\phi} \ sen \ \theta \ \vec{e}_\theta\right]\)            (9)

Assim, introduzindo as componentes cartesianas dos versores \(\overrightarrow{e}_\theta\) e \(\overrightarrow{e}_\phi\), obtemos:

\(L_z= m\ \ell^2 \ \dot{\phi} \ sen^2 \ \theta=\) constante

o que justifica a eq. (8).

Este sistema também conserva a energia mecânica: a tensão do fio não realiza trabalho e o peso deriva de uma energia potencial. Ora, a energia mecânica é:

\(E=\frac{1}{2}m\vec{v}^2 \ + \ mgz = \frac{1}{2}m \ \ell^2 \ (\dot{\theta}^{2} \ + \ \dot{\phi}^{2} \ sen^2 \ \theta)- mg\ell \ cos \ \theta\)             (10)

\(\frac{dE}{dt}=0\rightarrow m \ \ell^2 \ \dot{\theta} \ (\ddot{\theta}\ + \dot{\phi}^2 \ sen\ \theta \ cos \ \theta) \ + \ m \ \ell^2 \ \dot{\phi} \ \ddot{\phi} \ sen^2 \ \theta + mg\ell \ \dot{\theta} \ sen \ \theta = 0\)

Eliminando \(\ddot{\phi}\) pela eq. (7c), e simplificando o resultado, obtemos a eq. (7b).

Estes dois resultados mostram que as equações do movimento (7b) e (7c) são equivalentes, respetivamente, às conservações da energia mecânica e da componente vertical do momento cinético. Poderiamos, até, partir destas leis de conservação para deduzir rapidamente as equações do movimento. Não obteríamos, contudo, a eq. (7a) que fornece a tensão do fio, submetida à desigualdade expressa na eq. (1). É precisamente daqui que decorre uma grande riqueza de comportamentos do pêndulo como, a seguir, se analisa com alguns casos particulares.

a) Solução \(\theta ≡ \theta_0 =\) constante \(≠ 0\) (\(\theta_0 = 0\) não corresponde a qualquer movimento!)

A eq. (7c) dá:

\(\ddot{\phi}\ sen\ \theta_0=0 \ \rightarrow \ \ddot{\phi}=0\)

O pêndulo executa uma rotação circular em torno da vertical. Mas nem todas as configurações para tais rotações são possíveis; de facto, a eq. (7a) mostra que:

\(\frac{\tau}{m}=g\ cos\ \theta_0 \ + \ell \dot{\phi}^{2}\ sen^2\ \theta_0=g\ (cos\ \theta_0 + \frac{sen^2\ \theta_0}{cos \ \theta_0})= \frac{g}{cos\ \theta_0}\)

onde se usou a eq. (7b) para eliminar \(\dot{\phi}^2\). Assim, a condição (1) exige:

\(\tau \geq 0 \rightarrow \theta_0 \leq \frac{\pi}{2}\)

A FIGURA 4 exibe este movimento para o qual \(\dot{\phi}^2=\frac{g}{l \ cos \ \theta_0}\).

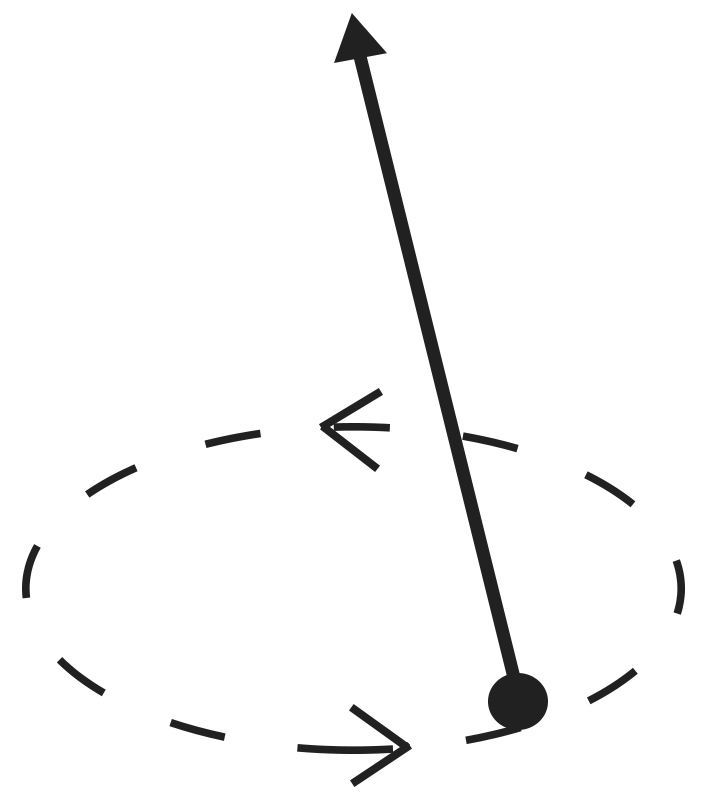
Que aconteceria se tentássemos fazer rodar o pêndulo acima do plano horizontal passando pelo ponto de suspensão, i.e., \(\theta_0 > \frac{\pi}{2}\) ? A eq. (1) seria violada: o fio não permaneceria esticado e a massa “cairia” para o interior da esfera imaginária, de centro naquele ponto e raio \(l\), o que nos obrigaria a discutir o movimento subsequente com mais um grau de liberdade (a distância à origem).

b) Solução \(\phi \ \equiv \ \phi_0 =\) constante \(\rightarrow L_z = 0\)

Agora, o plano do pêndulo é invariante, mas diversos comportamentos dinâmicos são possíveis, dependendo das condições iniciais. Reescrevamos as equações básicas sob a forma:

\(\frac{\tau}{ml}=\omega_0^2 \ cos \ \theta \ + \dot{\theta}^2 \geq 0\)

\(\ddot{\theta}+\omega_0^2 \ sen \ \theta =0 \rightarrow E =m\ell^2(\frac{\dot{\theta}^2}{2}-\omega_0^2 \ cos \ \theta)\)

onde:

\(\omega_0^2 \equiv \frac{g}{l}\)            (11)

   (i) Para oscilações de pequena amplitude (\(\theta << 1\)), é sempre \(\tau > 0\) e a equação de movimento reduz-se à equação de um oscilador harmónico de frequência natural \(\omega_0\):

\(\ddot{\theta}+\omega_0^2 \ \theta=0\)            (12)

Trata-se de um movimento oscilatório com aquela frequência.

   (ii) Consideremos, agora as seguintes condições iniciais:

\(\dot{\theta}(0)=0 \ \ \ \ \ \ \ \ \ \ \theta(0)=\theta_0\neq0\)

O pêndulo é largado com velocidade nula na posição \(\theta_0\), mas esta não pode ser qualquer porque o valor inicial da tensão, \(\tau(0)=ml \ \omega_0^2 \ cos \ \theta_0\), exige \(\theta_0\leq\frac{\pi}{2}\) o pêndulo não pode ser largado acima do plano horizontal passando pela origem. Uma vez assegurada esta condição, a conservação da energia mecânica dá, imediatamente, a velocidade:

\(\frac{\dot{\theta}^2}{2}=2\ \omega_0^2(cos\ \theta \ - \ cos \ \theta_0 )\)

Assim, a oscilação dá-se no intervalo \(-\theta_0 ≤ \theta ≤ \theta_0\), como se representa na FIGURA 5.

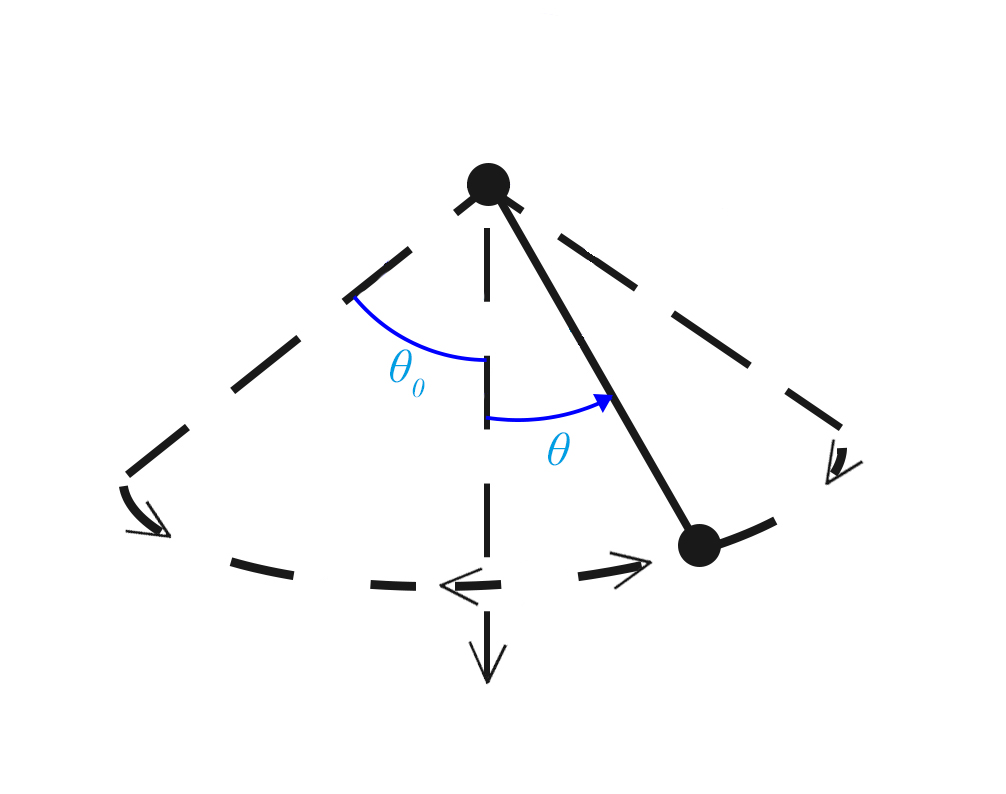
   (ii) Analisemos, agora, o que se passa com as condições iniciais:

\(\dot{\theta}^(0)=\dot{\theta}_0 \neq0 \ \ \ \ \ \ \ \ \ \ \theta(0)=0\)

Tal corresponde a dar um impulso ao pêndulo quando este se encontra na posição de equilíbrio. Da conservação da energia mecânica resulta:

\(\dot{\theta}^2=\dot{\theta}_0^2 - 2\ \omega_0^2 \ (1-cos\ \theta)\)            (13a)

Há várias hipóteses a considerar devido à condição sobre a tensão do fio:

\(\frac{\tau}{ml}=\dot{\theta}^2-\omega_0^2 \ (2-3cos \ \theta)\)            (13b)

1ª Se \(\dot{\theta}_0^2 \geq 5 \ \omega_0^2\) o pêndulo gira no plano vertical, efetuando um movimento circular (FIGURA 6). Com efeito, mesmo para \(\theta = \pi\), é \(\tau ≥ 0\) , tendo o pêndulo velocidade no seu ponto mais alto: \(\dot{\theta}^2=\dot{\theta}_0^2-4 \ \omega_0^2\) para \(\theta = \pi\). Trata-se, pois, de um rotação do pêndulo.

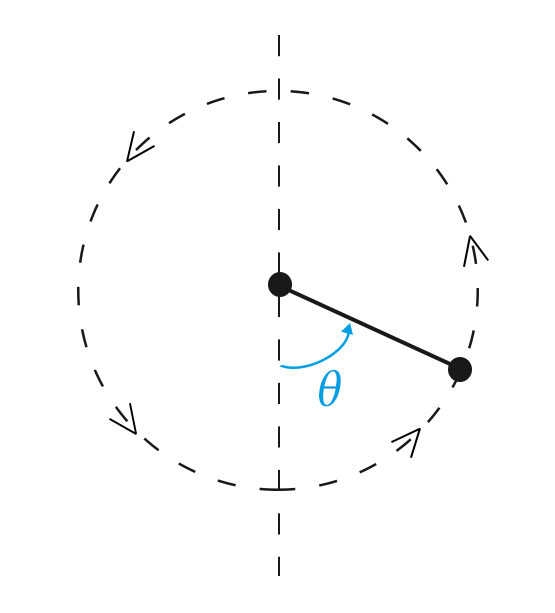
2ª Se \(2 \ \omega_0^2\ < \ \dot{\theta}_0^2\ < \ 5 \ \omega_0^2\), o movimento pendular não é possível porque a tensão anula-se numa posição \(\theta^*\) na qual o pêndulo ainda se move.

Com efeito, \(\theta^*\), para o qual é \(\tau = 0\), é determinado por \(cos\ \theta^* =\frac{1}{3}(2-\frac{\dot{\theta}_0^2}{\omega_2^0})\), vindo \(\theta^*\) real para \(\dot{\theta}_0^2\) no intervalo considerado. Mas, nesse ponto, é: \(\dot{\theta}^2 =\frac{1}{3}(\dot{\theta}_0^2-2 \ \ \omega_0^2)>0\). O anulamento da tensão, com o pêndulo ainda em movimento, significa que o fio deixa de estar esticado e a massa “cai” para o interior da esfera de raio l, passando a ter de ser descrito com os três graus de liberdade já referidos.

3ª Se \(0\leq \theta_0^.2\leq 2\ \omega_0^2\), o pêndulo executa um movimento oscilatório situado no intervalo \(-\theta_M \leq \theta \leq \theta_M\), onde \(\theta_M\) é o ponto onde se anula a velocidade, i.e.,

\(cos\ \theta_M = 1-\frac{\dot{\theta}_0^2}{2\omega_0^2}\geq0 \ \ \rightarrow \ \ 0<\theta_M\leq \frac{\pi}{2}\)

Nesse ponto, a tensão é não negativa:

\(\frac{\tau}{ml}=\omega_0^2 \ cos \ \theta_M \geq 0\)

Este caso contem, evidentemente, as pequenas oscilações atrás tratadas.

O pêndulo de Foucault

Qual o efeito da rotação da Terra no movimento de um pêndulo? Para um observador terrestre, somos obrigados a considerar as forças inerciais, destas, a única que importa é a força de Coriolis:

\(\vec{F}_c=-2m \ \vec{\omega}_T \ \times \vec{v}\)            (14)

onde \(\vec{\omega}_T\) é o vector rotação instantânea da Terra (Com efeito, a rotação da Terra pode ser considerada uniforme e com eixo fixo em escalas de tempo da ordem de milhares de anos; os outros termos das forças inerciais, exceto Coriolis adicionam a força centrífuga à força da gravidade, originando a definição de \(\vec{g}\) e a sua dependência na latitude). Vemos já, embora qualitativamente, que o plano de oscilação de um pêndulo não é mais invariante: a força de Coriolis, perpendicular à velocidade, obriga este plano a rodar. Procedamos à análise quantitativa considerando o caso habitual de pequenas oscilações, o que nos irá garantir que o fio permanece tenso. Para isso, é conveniente considerar, agora, um referencial cartesiano com origem no ponto de suspenção do pêndulo e com os eixos assim definidos (FIGURA 7):

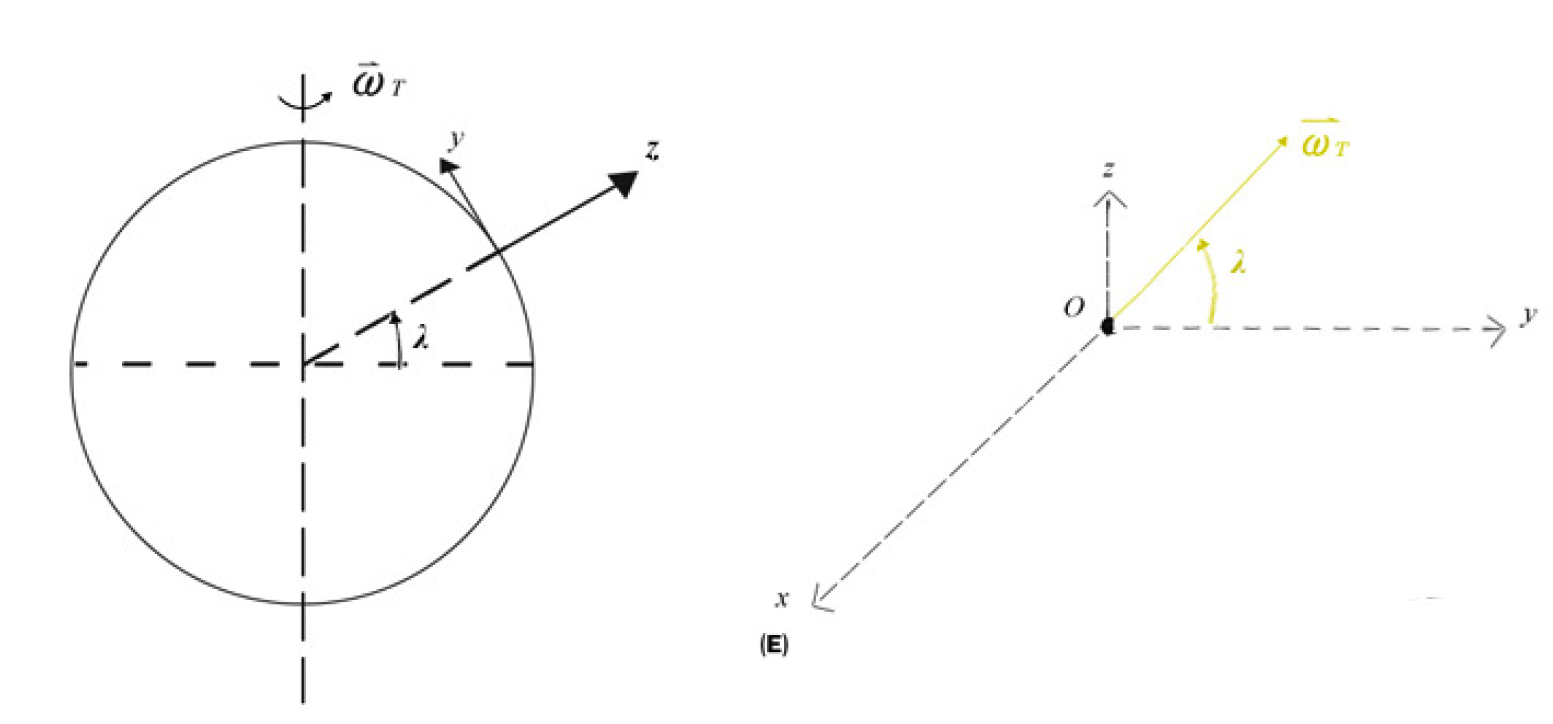
eixo \(z\): vertical do lugar (dirigido para cima)

eixo \(y\): tangente ao meridiano do lugar, apontando para Norte

eixo \(x\): tangente ao paralelo do lugar, apontando para Este.

Deste modo, o vector \(\vec{\omega}_T\) situa-se no plano (\(yz\)) fazendo um ângulo \(λ\) (latitude do lugar) com o eixo \(y\).

Para a análise do movimento, basta-nos estudar a evolução do momento cinético:

\(\frac{d\vec{L}}{dt}=\vec{M}=\vec{r}\ \times \ (m\vec{g}) - 2m\vec{r} \ \times \ (\vec{\omega_T} \ \times \ \vec{v})=\vec{r} \ \times (m\vec{g})+2m \ \vec{r} \cdot \vec{\omega}_T \ \vec{v}\)

onde se atendeu a que \(\vec{r}\cdot\vec{v}=0\) (fio permanece esticado). Usando a expressão do momento cinético atrás obtida, eq. 9, é imediato escrever as equações do movimento:

\(\ddot{\theta}-\dot{\phi}^2 \ sen \ \theta \ cos \ \theta = -\omega_0^2 \ sen \ \theta - 2 \ (\vec{e}_r\cdot\vec{\omega}_T) \ \dot{\phi} \ sen\ \theta\)            (15a)

\(2 \ \dot{\phi} \ \dot{\theta} \ cos \ \theta \ + \ \ddot{\phi} \ sen \ \theta =2 \ (\vec{e}_r\cdot\vec{\omega}_T) \ \dot{\theta}\)            (15b)

estas equações generalizam as eqs. (7b) e (7c) ao incluírem os efeitos da rotação da Terra.

Ora, \(\vec{\omega}_T\) tem as componentes cartesianas \(\vec{\omega}_T= \omega_T \ (0, cos \ \lambda, sen \ \lambda)\), pelo que:

\(\vec{e}_r \cdot \ \vec{\omega}_T= \omega_T \ (cos \ \lambda \ sen \ \theta\ cos \ \phi \ -sen \ \lambda \ cos \ \theta)\)

Para pequenas amplitudes de oscilação do pêndulo (\(\theta << 1\)), vem:

\(\vec{e}_r \cdot \ \vec{\omega}_T \cong - \ \omega_T \ sen \ \lambda\)

pelo que a eq. (15b) admite a solução:

\(\phi^.=- \ \omega_T \ sen \ \lambda\) = constante             (16)

(Para uma dedução mais simplificada deste resultado, ver “Pêndulo de Foucault”)
Quer dizer, o plano do pêndulo roda, em torno da vertical, no sentido dos ponteiros do relógio no hemisfério Norte (\(\lambda > 0\)) e no sentido contrário no hemisfério Sul (\(\lambda < 0\)). Esta rotação é uniforme e informa diretamente sobre a latitude do lugar, como se mostra na FIGURA 8.

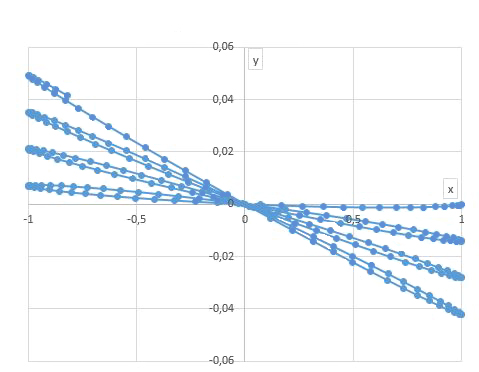
Finalmente, a eq. (15a) mostra que o período de oscilação do pêndulo é alterado:

\(\omega_0 \ \ \ \ \ \ \rightarrow \ \ \ \ \ \ \sqrt{\dot{\phi}^2 +\omega_0^2}\)

Porém, esta alteração é, praticamente, impercetível para as condições experimentais habituais ( \(ω_0 >> ω_T\)).

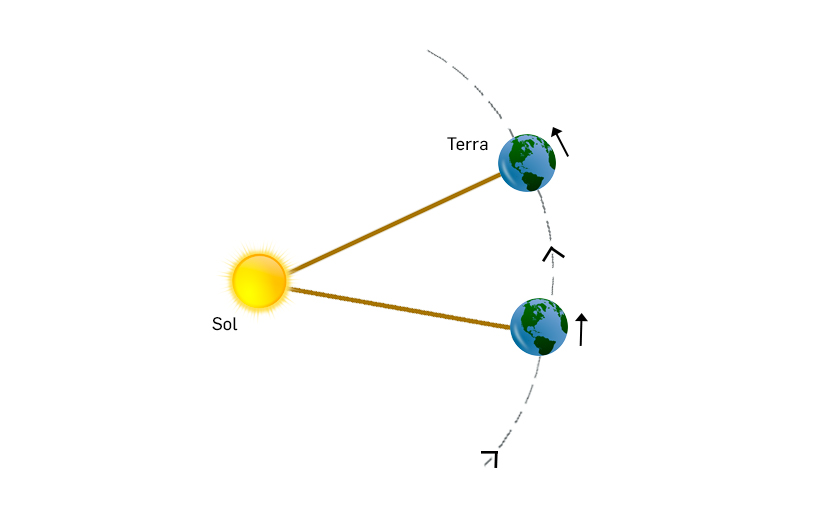
Tem interesse, neste contexto, analisar o valor de \(ω_T\). Como a Terra efetua uma rotação completa em 24h, poder-se-ia pensar que \(ω_T\approx\frac{2\pi}{24\times3600}s^{-1}\).Mas não é assim! Com efeito, um dia, i.e., 24 h é o tempo que decorre, para um observador na Terra, para o mesmo ponto do planeta se encontrar alinhado com o Sol. Mas, durante esse tempo, a Terra também se deslocou no seu movimento de translação em torno do Sol, que também é uma rotação. Para simplificar, aceitemos que este movimento é circular uniforme, realizando-se no mesmo sentido que a rotação da Terra (FIGURA 8). Então, ao fim de 24 h, a Terra rodou um pouco mais que \(2\pi\) e este excesso acumula-se exatamente em \(2\pi\) ao fim de um ano, quando a Terra regressa à sua posição inicial. Quer dizer, para um observador no Sol, considerado como observador inercial para quem \(\omega_T\) é definido, a Terra rodou 366 vezes no tempo correspondente a 365 dias terrestres, i.e., \(\frac{366}{365}\) vezes po dia terrestre, pelo que:

\(\omega_T\approx\frac{2\pi}{24\times3600}\times\frac{366}{365}s^{-1}\approx 7.3 \times 10^{-5} \ s^{-1}\)