Como exemplo, tomemos para um primeiro referencial o de uma estação de comboio —ou seja, um referencial definido por objetos em repouso na estação—, e para um segundo o de uma carruagem que acelera em relação à estação, em linha reta, com uma aceleração \( \overrightarrow{a_{c}} \).

Um bloco de madeira pousado numa mesa da carruagem estará imóvel nesse referencial, mas terá aceleração no referencial da estação. O observador Zé, no referencial da estação, aplicando a segunda lei de Newton, dirá que sobre o bloco se exerce uma força igual ao produto da sua massa pela sua aceleração, \( \overrightarrow{F} = m \times \overrightarrow{a_{c}} \).

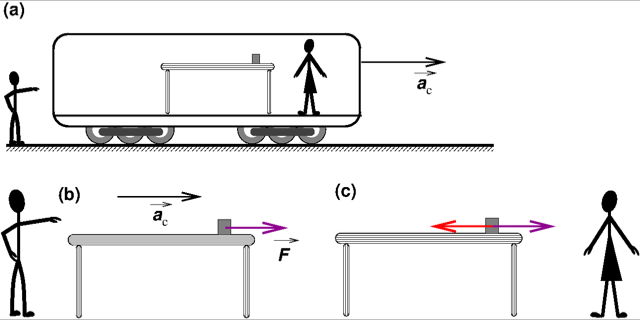
Figura 1. (a) Um bloco que não se desloca sobre a mesa está imóvel para a Ana, mas tem aceleração \( \overrightarrow{a_{c}} \) para o Zé;(b) O Zé conclui que existe uma força \( \overrightarrow{F} = m \times \overrightarrow{a_{c}} \) a atuar no bloco. Essa força só pode ser a força de atrito estático com a mesa; (c) a Ana vê o bloco parado. Logo conclui que a resultante das forças é nula. Existe uma força adicional \( \overrightarrow{F} = - m \times \overrightarrow{a_{c}} \) que cancela a de atrito.

Qual é a origem dessa força? O único corpo em interação com o bloco é a mesa. A força de interação entre duas superfícies sólidas paralela à superfície de contacto é a força de atrito. É pois a força de atrito exercida pela mesa que arrasta o bloco com a mesma aceleração que a mesa.

Mas uma observadora dentro da carruagem, a Ana, verá o bloco em repouso, com velocidade e aceleração nulas: o bloco tem uma posição fixa em relação à carruagem. Se aplicar a segunda lei, concluirá que a resultante das forças que actua no bloco é nula. A diferença entre as forças que reta no mesmo corpo (bloco) nos dois referenciais é

\( \left[ \overrightarrow{F} \right]_{carr} - \left[ \overrightarrow{F} \right]_{est} = \overrightarrow{0} - m \overrightarrow{a_{c}} = - m \overrightarrow{a_{c}} \)

No referencial da carruagem existe uma força adicional \( -m \overrightarrow{a_{c}} \), em relação às do referencial da estação:

\( \left[ \overrightarrow{F} \right]_{carr} = \left[ \overrightarrow{F} \right]_{est} - m \overrightarrow{a_{c}} \)

Alguns autores designam estas forças por forças fictícias ou pseudo forças (Feynman, 1963). A força que atua no corpo no referencial da estação é devida a uma interação entre a mesa e o bloco: atua num corpo (bloco) e é exercida por outro (mesa). No referencial da carruagem, além desta força de interação, existe uma outra, \(-m \overrightarrow{a_{c}}\), que, ao contrário da força de atrito, não tem origem numa interação física entre dois corpos. Este ponto de vista considera que essa força não é real e resulta apenas de uma “tentativa” de aplicar a segunda lei de Newton, num referencial em que ela não se aplica. Isto leva-nos a distinguir dois tipos de referenciais. Nos referenciais inerciais todas as forças são “reais”, com origem nas interações físicas com outros corpos; tendencialmente essas forças diminuem com o afastamento entre os corpos em interação. Nestes referenciais a segunda lei de Newton é válida: a resultante de todas as forças “reais” que atuam num corpo é o produto da sua massa pela sua aceleração. Os referenciais não inerciais são acelerados em relação aos inerciais. Nestes a segunda lei não é válida, na medida em que se a tentarmos aplicar, teremos de supor a existência forças adicionais, fictícias, que não têm origem na interação física entre corpos.

Este ponto de vista tem um inconveniente: em experiências feitas localmente é muito difícil determinar se o nosso referencial é, ou não, inercial. Para compreender esta afirmação, imaginemos que a Ana não tem janelas para ver para fora da carruagem e faz um conjunto de experiências para determinar se o seu referencial é inercial.

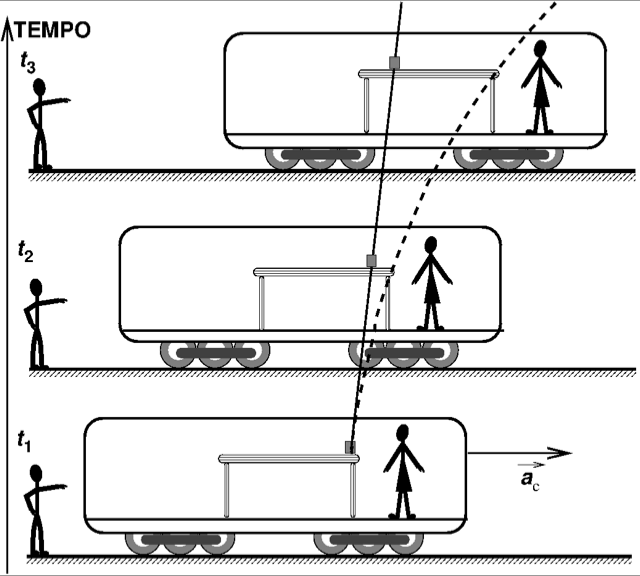
Figura 2. Para o Zé, na estação, quando o cubo de gelo é pousado na ponta da mesa, tem a mesma velocidade que a carruagem. Como não existe força de atrito com a mesa, a partir daí o Zé vê o bloco a deslocar-se com velocidade constante, igual à sua velocidade inicial (linha a cheio). Mas a carruagem, a mesa e a Ana estão a acelerar, ou seja a sua velocidade está a aumentar em relação ao Zé (linha a tracejado). A Ana observa o bloco a acelerar para trás sobre a mesa.

Começa por pousar na mesa um cubo de gelo que não tem atrito com a mesma (Figura 2). Para o Zé, a resultante das forças sobre o cubo é nula (o atrito com a mesa é nulo). Depois de pousado, desloca-se a velocidade contante: aquela que o comboio tinha quando o cubo foi pousado na mesa. Mas a velocidade da carruagem está aumentar por que esta está a acelererar na direção do movimento: por isso o cubo fica para trás. A Ana, dentro da carruagem vê o cubo a acelerar na direção oposta à do movimento da carruagem em relação à estação.

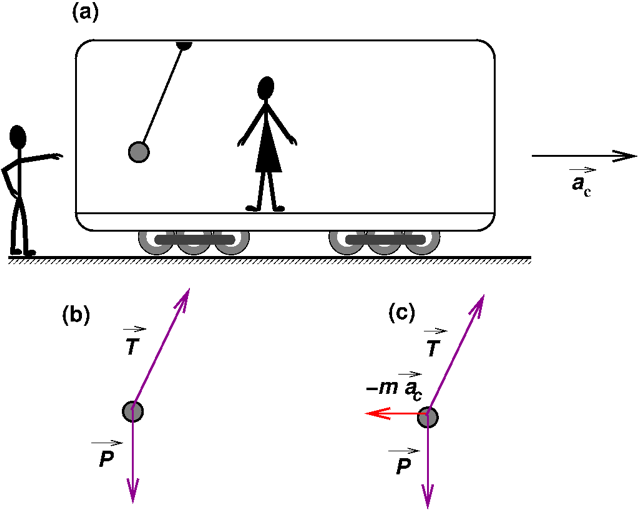
Figura 3. (a) Um corpo pendurado no teto não ficará perpendicular ao chão da carruagem; (b) o observador da estação vê o corpo acelerado e conclui que o seu peso, \( \overrightarrow{P} \), e a tensão do fio de suspensão, \( \overrightarrow{T} \) têm uma resultante \( \overrightarrow{P} + \overrightarrow{T} = m \overrightarrow{a_{c}}\); (c) a obervadora da carruagem vê a esfera em respouso; daí conclui que existe uma força adicional \( -m \overrightarrow{a_{c}} \) que, somada a \( \overrightarrow{P} \) e a \( \overrightarrow{T} \) dá resultante nula.

Seguidamente, a Ana pendura uma esfera num fio que prende ao teto (Figura 3). O fio não ficará perpendicular ao chão da carruagem. No referencial da estação a esfera terá a mesma aceleração que a carruagem, \( \overrightarrow{a_{c}} \). Sobre ela atuam duas forças: o peso com direção vertical, e a tensão do fio de suspensão. A soma destas duas forças terá de dar uma resultante \( \overrightarrow{F} = m \overrightarrow{a_{c}} \), o que implica que o fio tenha uma inclinação em relação à vertical da estação. Mas um fio com um “peso” na ponta chama-se fio de prumo e define a vertical do lugar. A Ana apenas descobrirá que a sua “vertical” (direção do fio de prumo) não é perpendicular ao chão: este não está “horizontal”.

Estas diferenças na descrição do mesmo fenómeno entre os dois referenciais radicam no facto de as acelerações do mesmo corpo serem distintas. Um corpo em repouso no referencial da carruagem tem aceleração \( \overrightarrow{a_{c}} \) no da estação. Em geral, se for \( \overrightarrow{a} \) a aceleração no referencial da estação, a aceleração no referencial da carruagem será:

\( \overrightarrow{a'} = \overrightarrow{a} - \overrightarrow{a_{c}} \)

Ora, não existe na carruagem nenhum letreiro onde se leia:


Referencial Não Inercial. Cuidado com Segunda Lei!


As forças são medidas e sentidas pelos seus efeitos nos corpos, nomeadamente pela aceleração dos mesmos. Por isso, a Ana, na carruagem, deteta no seu referencial uma força extra, em relação às da estação,

\( \left[ \overrightarrow{F} \right]_{carr} = m \overrightarrow{a'} = m \overrightarrow{a} - m \overrightarrow{a_{c}} = \left[ \overrightarrow{F} \right]_{est} - m \overrightarrow{a_{c}} \)

Como interpreta esta observação?

O Zé, na estação, sabe que além das forças de interação entre os objetos que manipula, todos os corpos estão sujeitos ao peso,

\( \overrightarrow{P} = m \overrightarrow{g} \).

A Ana verifica, de modo semelhante, que todos os objetos no seu referencial estão sujeitos a uma força

\( \overrightarrow{P'} = m \overrightarrow{g'} = m \overrightarrow{g} - m \overrightarrow{a_{c}} \)

em que \( \overrightarrow{g'} = \overrightarrow{g} - \overrightarrow{a_{c}} \). Ela não descobrirá que está num referencial não inercial, apenas que a aceleração da gravidade no seu referencial é \( \overrightarrow{g'} \), em vez de \( \overrightarrow{g} \). O seu chão não está na horizontal— que é a direção perpendicular a \( \overrightarrow{g'} \)—, e as suas paredes não estão verticais—direção do fio de prumo. O cubo de gelo deslizou sobre a mesa porque o tampo da mesa está inclinado em relação à direção horizontal, que, quer para ela, quer para o Zé, é a direção perpendicular à do fio de prumo. É possível que fique um pouco desorientada pelas paredes da carruagem não serem paralelas à direção do fio de prumo nem o chão perpendicular ao mesmo. A força inercial também atua na Ana, e o seu equilíbrio, na posição em que está representada nas figuras 1 a 3, será um pouco precário: se a direção de \( \overrightarrow{g'} \) intersetar o chão fora da base de apoio definida pela posição dos seus pés, ela tombará. Mas se a imaginarmos colocada numa cabine inclinada em relação à estação (Figura 4), com orientação determinada pela direção de \( \overrightarrow{g'} \), ela terá uma experiência em tudo idêntica à do Zé, apenas como um valor da aceleração da gravidade maior,

\( g' = \sqrt{g^{2} + a_{c}^2} \)

O fio de prumo estará paralelo às paredes; o cubo de gelo ficará imóvel na mesa; se largar uma bola ela cairá junto dos seus pés, na direção do fio de prumo; a água numa bacia terá uma superfície perpendicular à direção de \( \overrightarrow{g'} \). Se se pesar numa balança, descobrirá que o seu peso aumentou desde que subiu para a carruagem1

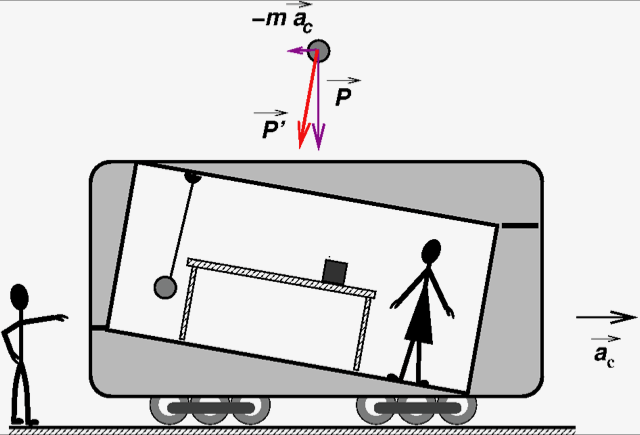
Figura 4. Para a observadora da carruagem a aceleração da gravidade tem a direção de \( \overrightarrow{P'} \). Ela está confortavelmente de pé com o corpo paralelo à direção do fio de prumo. O bloco não desliza na mesa porque o tampo está horizontal, perpendicular à direção da aceleração da gravidade no referencial da carruagem.

Esta impossibilidade de decidir se um referencial é não inercial fica ainda mais clara se imaginarmos que houve um engano na figura 4: afinal a situação real é a da figura 5.

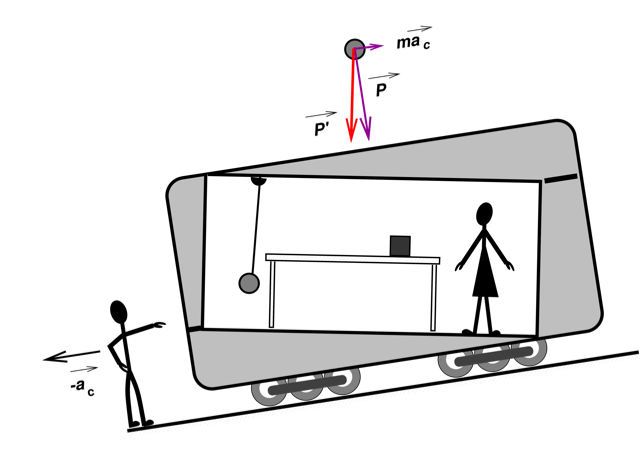
Figura 5. As experiências acima relatadas são compatíveis com a situação desta figura: a carruagem está parada numa rampa e o Zé está acelerado.

A carruagem está parada numa rampa e o Zé está acelerado na direção oposta com aceleração \( -\overrightarrow{a_{c}} \). Toda as observações referidas na Figura 4 são compatíveis com esta situação. Só que agora é no referencial da Ana que a aceleração da gravidade é a “real”, devida à atração da Terra, e a do Zé inclui uma força inercial \( -m(-\overrightarrow{a_{c}}) = m \overrightarrow{a_{c}} \). Afinal qual é o referencial inercial?

A lição destas observações é que, localmente, numa região limitada do espaço e tempo, forças inerciais não se podem distinguir de forças gravíticas. Quer umas quer as outras, atuam universalmente em todos os corpos, proporcionalmente à respetiva massa, razão pela qual conferem a todos os corpos a mesma aceleração.

Esta ideia constitui o princípio de equivalência e é a base física da Teoria da Relatividade Geral de Einstein. As equações da Relatividade Geral têm a mesma forma em qualquer referencial e o conceito de referencial inercial perde sentido. O movimento de corpos livres de forças que não as gravíticas é determinado pela geometria do espaço-tempo e esta depende, quer da distribuição de matéria, quer do referencial. A impossibilidade de distinguir forças inerciais da gravitação é expressa pela existência de referenciais em que, localmente, a aceleração gravítica é nula: referenciais de queda livre. Estes existem mesmo na vizinhança de massas criadoras de um campo gravítico. Um exemplo é a Estação Espacial Internacional (EEI). Como se move com a aceleração do campo gravítico da Terra, no seu referencial as forças inerciais cancelam exatamente a atração gravítica da Terra: os objetos não têm peso e no interior da EEI a gravidade é nula.

No contexto da fisica Newtoniana, podemos, em princípio, distinguir as forças que têm origem nas interações entre corpos das forças inerciais e designar estas por fictícias. Este é o ponto de vista apresentado em quase todos os manuais de Física (Lage, 2015). Mas devemos ter em conta que os efeitos das forças “fictícias” são tão reais como os de uma força “legítima” como a força da gravidade. Tanto assim que é impossível distingui-las através de experiências realizadas localmente. Por essa razão, este autor prefere a designação de força inercial: para um obervador que as experimenta, os seus efeitos são idênticos aos de qualquer outra força.

Neste breve artigo não referimos a situação mais complexa de referenciais em rotação mútua. Nesse caso as forças inerciais incluem a força centrífuga, função apenas da posição do corpo, e a força de Coriolis, que depende da sua velocidade. Numa nave espacial que se movimente apenas sob ação da gravidade, tal como na EEI, não existe peso. Mas com a nave em rotação, a força centrífuga pode ter exactamente o efeito de uma força gravítica. Este é o processo que permite criar “gravidade artificial”, e aproximar o ambiente de uma nave espacial da experiência que temos na Terra.


Notas

1 Em compensação, se a carruagem acelerar numa descida, o seu peso diminuirá, porque a força inercial, \( -m \overrightarrow{a_{c}} \), cancelará parcialmente a da gravidade. Mas o que muda é \( g \), não a massa.


Agradecimentos

Agradeço à Dra. Ana Rita Mota várias sugestões de melhoramento deste texto.