Sendo a Física uma disciplina em que, de forma geral, os alunos apresentam grandes dificuldades, este cenário fica crítico quando pretendemos ensinar Física a alunos com profundas lacunas em conceitos basilares da Física e da Matemática. Assim, e provavelmente por essa mesma razão, para esses alunos, as aulas desta disciplina são território árido, inacessível e desprovido de qualquer significado e interesse. Este é tradicionalmente o caso típico de muitos alunos do Ensino Profissional, que encaram a Física como uma ciência abstrata suportada por representações matemáticas que não dominam, na qual é “preciso decorar fórmulas cuja origem e finalidade são desconhecidas” (Veit & Teodoro, 2002, p. 88) numa teia de enorme complexidade, inibindo-lhes a atenção na aula e o interesse nesta disciplina. Feito o diagnóstico, impõe-se criar pontes entre os conceitos da Física e os fenómenos físicos do quotidiano e estabelecer, de forma visual, uma relação direta entre estes mesmos fenómenos físicos e as representações matemáticas, sejam elas gráficas ou algébricas. Pegar e lançar uma bola a um aluno, algures na sala, e vê-lo a agarrar a bola em pleno voo, e dizer “Este aluno sabe Física! Ele soube o momento e a posição exata onde colocar a mão pela perceção do movimento da bola” pode ser uma boa forma de quebrar o gelo e criar empatia, mas há agora que vestir este acontecimento com a roupagem matemática e descobrir todas as caraterísticas do movimento. Mas como passar do fenómeno físico à representação matemática? A minha sugestão chama-se Análise Digital de Vídeo e dela darei testemunho com um tema pouco simples como é a Cinemática para alunos do 11ºano dos Cursos Profissionais na Escola Secundária Adolfo Portela - Águeda.

A Análise Digital de Vídeo é uma técnica que permite analisar o movimento de um objeto presente num vídeo que contenha ainda uma referência espacial e do qual se conheça a escala de tempo na qual se registou o movimento. Com estes elementos e recorrendo a uma aplicação informática específica para este fim, consegimos extrair do vídeo tabelas de dados e respetivas representações gráficas. Deste modo, o aluno acompanha a posição do corpo em cada instante durante o movimento, com as respetivas coordenadas nas representações gráficas no instante considerado, de forma simultânea e síncrona, permitindo-lhe avançar depois para as suas representações analíticas que traduzem as leis cinemáticas do movimento. No caso concreto deste trabalho, recorri ao Tracker, um software gratuíto disponibilizado por Douglas Brown, de Cabrillo College, (http://www.cabrillo.edu/~dbrown/tracker/). Esta aplicação permite ainda a realização de estudos exploratórios através da modelação matemática, alterando as condições do movimento e sobrepondo ao vídeo objetos virtuais animados de acordo com as caraterísticas definidas pelo aluno e/ou professor. Percebido o conceito, fica assim ao alcance do professor a possibilidade de realizar uma abordagem de elevado potencial pedagógico, capaz de envolver os alunos, bastando para isso recorrer a um simples telemóvel com câmara de vídeo, um computador e uma aplicação informática de análise digital de vídeo. O mundo à nossa volta transforma-se num poderoso laboratório de Cinemática e Dinâmica.

O desafio começou por disponibilizar 10 minutos da aula para vir ao exterior e registar em vídeo alguns lançamentos com uma bola de basquetebol, tendo o cuidado de ter em cena um metro graduado que servisse posteriormente de escala. Feitos vários registos regressámos à sala onde transferimos os vídeos para o computador, importando-os no Tracker.

Defini o referencial e a escala, bem como a porção do vídeo a explorar, explicando a importância de cada um destes elementos no processo, sob o olhar curioso e atento dos alunos que iam colocando questões e, sem darem conta, aprendendo conceitos. Criado o objeto a marcar, fotograma a fotograma, obtém-se uma tabela de valores de posição x e y em função do tempo, bem como todos os parâmetros que daqui decorrem. Simultaneamente poderemos ter visíveis até três gráficos diferentes em simultâneo, ferramenta fundamental ao estudo da cinemática, mas de difícil análise para os alunos que tendem a confundir a representação gráfica do movimento com a imagem do próprio movimento (Beichner, 1994). Temos assim a possibilidade de relacionar a informação nos diferentes gráficos, confrontando-a em cada instante, não só entre si, como com o respetivo fotograma do vídeo do movimento em estudo.

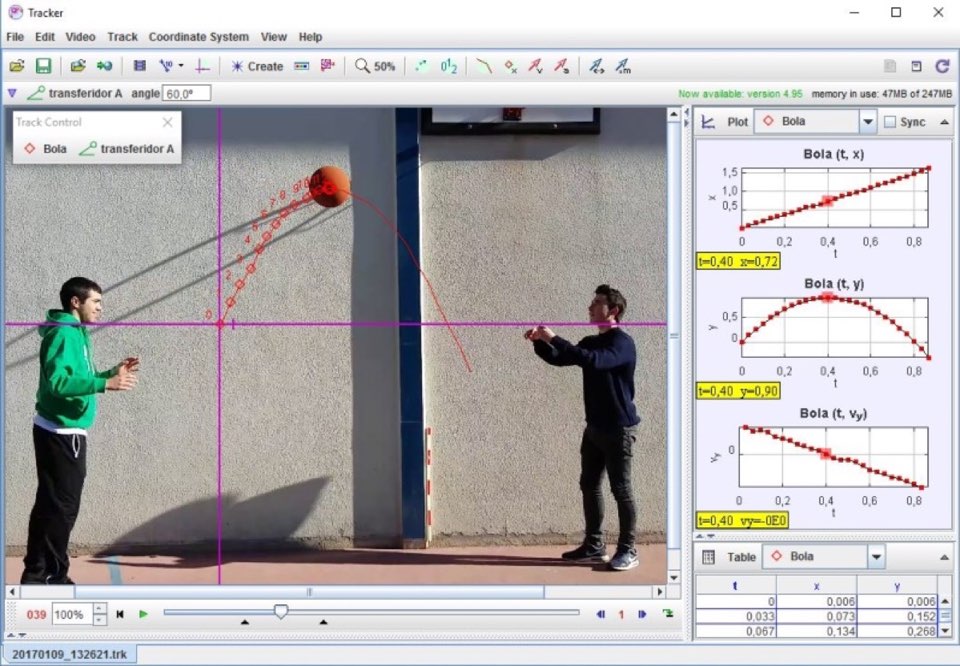
Neste caso, escolhi três gráficos. No primeiro, \( x = f(t) \) ilustra a variação da posição horizontal em função do tempo. Percebendo tratar-se de uma reta, o aluno percebe que neste eixo iguais espaços são percorridos em iguais intervalos de tempo, logo a velocidade do movimento na horizontal é constante. O segundo gráfico, \( y = f(t) \), mostra que na vertical o comportamento da bola é definido por uma parábola. Logo, a posição vertical obedece a uma equação quadrática caraterística da equação das posições¹ num movimento retilíneo uniformemente variado, com uma aceleração não nula (neste caso de valor negativo face à concavidade da parábola). Escolhi ainda acrescentar um terceiro gráfico, \( v_{y} = f(t) \), que evidencia que, tanto na subida como na descida, o declive (que traduz a componente escalar da aceleração) é constante. Isto raramente é óbvio para os alunos, podendo a partir daqui repescar a Lei Fundamental da Dinâmica e salientar que nas presentes circunstâncias, a força a que a bola está sujeita é também constante. O instante que escolhi nesta imagem corresponde ao instante em que a bola atinge a altura máxima na sua trajetória, podendo assim confrontar os gráficos \( y = f(t) \) e \( v_{y} = f(t) \) (2º e 3º gráficos da imagem) e salientar que a componente vertical da velocidade é nula no instante em que a altura atingida pela bola foi máxima. Este ambiente exploratório permite esclarecer dúvidas dos alunos e criar espaço de discussão sobre a física do movimento, seja na vertente cinemática, seja na vertente dinâmica.

Colocadas as equações do movimento no quadro, é tempo para avançar para análise algébrica dos gráficos apresentados. Com tempo seria adequado serem os alunos a descobrir os parâmetros do movimento e a escreverem as equações do movimento em causa. Se não houver tempo, ou se a opção didática for outra, o Tracker dispõe de uma ferramenta de análise gráfica bastante interessante: Data Tool.

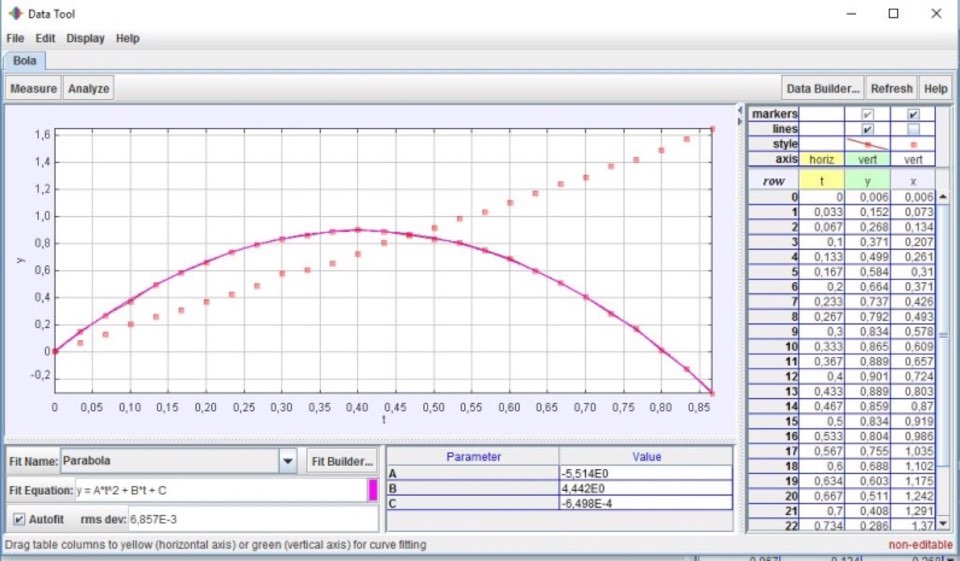
Uma vez definidas as equações do movimento podemos pedir ao aluno que determine, o tempo de subida, a altura máxima atingida, o instante em que a bola atinge o solo e a respetiva componente escalar da sua velocidade, e confrontar essas determinações com os valores patentes nos gráficos.

A Análise Digital de Vídeo constitui uma estratégia didática que estreita a relação entre o fenómeno físico quotidiano e as suas representações matemáticas, promovendo aprendizagens significativas e envolvendo os alunos no processo. Neste caso, a estratégia foi aplicada a turmas de Cursos Profissionais cujos alunos são tradicionalmente pouco motivadas para o estudo da Física e que tiveram aqui uma motivação acrescida que os fez acompanhar a aula e lhes deu oportunidade de aprender Física.

Notas

¹ \( y = y_{0} + v_{0}t + \frac{1}{2} a t^2 \)