A European Schoolnet, uma rede de 31 Ministérios da Educação incluindo o português, refere a urgência do aumento da literacia dos cidadãos europeus em STEM (Science, Technology, Engineering and Mathematics). Quanto mais não seja, neste contexto fará sentido que os nossos alunos do ensino secundário sejam colocados perante alguns métodos numéricos de resolução de equações, cujas vantagens de integração curricular precoce era já referida pelo notável pedagogo Sebastião e Silva há mais de 40 anos. Promover o desenvolvimento do sentido crítico é tarefa de qualquer agente educativo e ser crítico na utilização de máquinas de cálculo, por exemplo, baseadas no uso de métodos numéricos, deverá ser também tarefa de professores de diferentes áreas, com particular destaque para os de matemática, até porque as máquinas de cálculo, como máquinas de calcular ou mesmo os mais sofisticados computadores efetuam cálculos numéricos inevitavelmente sujeitos a erros.

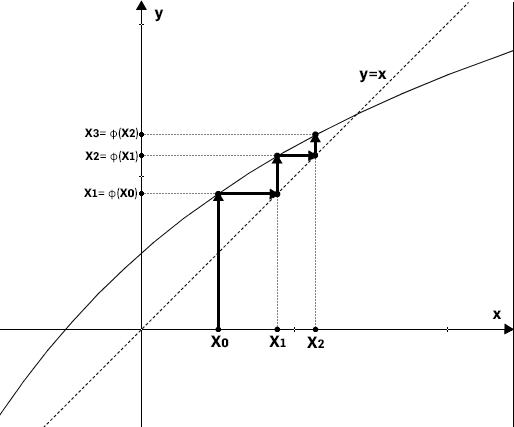
Um método numérico de resolução de equações de grande potencial pedagógico é o método do ponto fixo, que consiste em obter uma sucessão convergente para uma solução de uma equação do tipo x = ϕ(x), designando-se ϕ por função iteradora.

Por exemplo, a equação \(x^2 = 2\) é equivalente à equação \(x =\frac{4x+2}{x+4}\) , pelo que se pode neste caso definir a função iteradora \(ϕ(x) =\frac{4x+2}{x+4}\) . Esta é uma função iteradora que permite a construção de uma sucessão convergente para o ponto fixo √2, podendo observar-se na FIGURA 1 um esquema gráfico da construção dos termos da sucessão e os primeiros doze termos da sucessão quando se inicia com \(x_0 = 0,5\).

Herão de Alexandria (FIGURA 2), geómetra e engenheiro grego, que viveu muito provavelmente no Séc. I, tinha de resolver muitos problemas envolvendo raízes quadradas na sua prática de engenharia e para tal utilizava o método que a seguir se descreve, que não terá inventado, mas que hoje em dia se conhece pelo seu nome (também designado por método babilónico).

Para determinar um valor aproximado de √2, por exemplo, considerava uma aproximação fácil de obter, seja 1. De seguida, calculava a média dessa aproximação com o quociente do radicando por essa aproximação. Com o valor obtido, uma nova aproximação, efetuava sucessivamente o mesmo procedimento e considerando este exemplo podem observar-se as primeiras três aproximações calculadas.

\( x_0 = 1\)     ;     \(x_1=\frac{1+\frac{2}{1}}{2}=1,5\)     ;     \(x_2=\frac{1,5+\frac{2}{1,5}}{2} =1,41(6)\)     ;     \(x_3=\frac{x_2+\frac{2}{x_2}}{2} =1,414215...\)

Note-se que bastaram duas iterações deste método para obter √2 com precisão superior à da 7ª iteração com a função iteradora considerada no método do ponto fixo. O que o método de Herão tem de curioso é que é também um método de ponto fixo, mas com uma função iteradora mais poderosa no sentido da rapidez de convergência. \(ϕ(x) =\frac{1}{2} \left(x+\frac{2}{x}\right)\).

Isto revela que a eficácia do método do ponto fixo depende, entre outros fatores, de uma boa escolha de uma função iteradora. É possível reduzir um pouco os graus de liberdade para boas escolhas considerando um resultado que diz que a sucessão \(x_{n+1} = ϕ(x_n)\) é convergente para um ponto fixo ρ no interior de um intervalo I se em I ϕ for diferenciável e |ϕ´(x)| < 1. Além disso, a convergência é tanto mais rápida quanto mais próximo de zero se encontrar |ϕ’(ρ)|. Na realidade, enquanto no primeiro caso se tem \(ϕ'(x) =\frac{14}{x^2+8x+16}\) , no método de Herão tem-se que \(ϕ'(x) =\frac{x^2-2}{2x^2}\), donde se pode concluir que ϕ´(√2) é maior que zero (e menor do que 1) no primeiro caso, mas igual a zero no segundo caso.

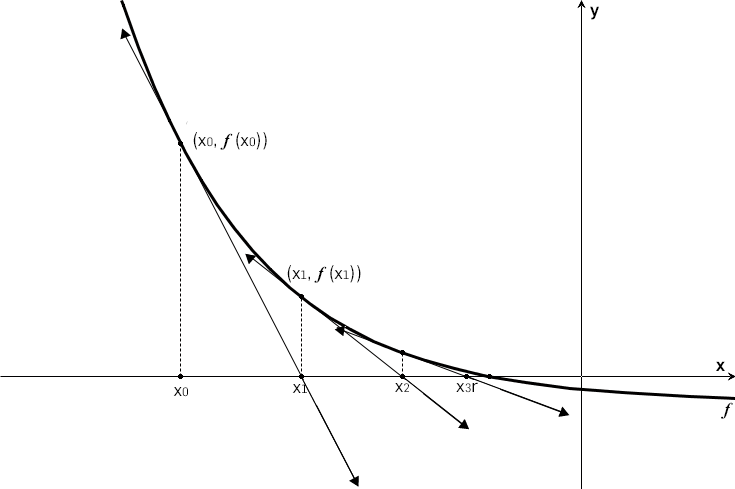
Outro método numérico de resolução de equações, que quando funciona é excelente em termos de eficácia, é o método de Newton-Raphson.

Tem uma interpretação geométrica muito interessante, baseada em interseções de retas tangentes ao gráfico da função com o eixo das abcissas do referencial, como se pode observar na FIGURA 3. Neste método, o termo geral da sucessão de iterações que se obtém é \(x_{n+1} = x_n -\frac{f(x_n)}{f'(x_n)}\).

Pode observar-se na FIGURA 3 que, neste método, à quarta iteração já são pelo menos onze as casas decimais exatas e os sucessivos valores parecem ser os mesmos do método de Herão. Na realidade assim é, pois ao resolvermos a equação \(f(x)=0\) e ao considerarmos a função iteradora \(ϕ(x) = x -\frac{f(x)}{f'(x)}\) , temos o método de Herão. Podemos observar deste modo que o Método de Newton-Raphson é, em circunstâncias que permitam a convergência, um caso particular do método do ponto fixo, que apresenta uma função iteradora que permite a mais rápida convergência.

Alguns dos aspetos referidos foram integrados com eficácia em aulas do 11º e do 12º anos de escolaridade, permitindo um melhor foco nas aprendizagens das sucessões, das derivadas, dos limites, entre outros, e uma maior satisfação das necessidades dos alunos mais curiosos e sedentos de sabedoria.