Função quadrática
📧 , 📧
- * Faculdade de Ciências da Universidade do Porto
- ɫ CMUP/ Universidade do Porto
Referência Tavares, J.N., Geraldo, A., (2017) Função quadrática, Rev. Ciência Elem., V5(1):069
DOI http://doi.org/10.24927/rce2017.069
Palavras-chave função quadrática, números reais, parábola, equação do 2º grau
Resumo
Uma função \(f: \mathbb{R} \longrightarrow \mathbb{R}\) chama-se uma função quadrática quando existem números reais \(a\), \(b\) e \(c\), com \(a \neq 0\), tais que \(f(x)=ax^2+bx+c\) para todo \(x \in \mathbb{R}\).
Propriedades
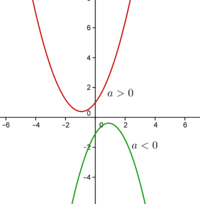
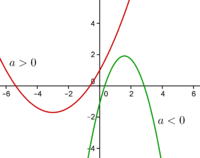
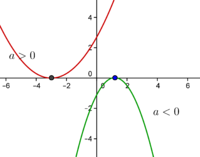
A função quadrática tem no máximo dois zeros. Determinar os zeros de uma função quadrática é equivalente a resolver a equação do 2ºgrau \(ax^2+bx+c=0\), assim poderá ser necessário recorrer à fórmula resolvente para equações do 2ºgrau.
|
|
 |
 |
 |
Monotonia:
| Suponhamos \(a>0\) e consideremos a forma canónica para a função quadrática \(f(x)\),
\(\displaystyle f(x)=ax^2+bx+c=a\left[ \left( x+\frac{b}{2a} \right)^2+ \frac{4ac-b^2}{4a^2} \right]\) Considerando a soma da duas parcelas no interior dos parêntesis retos, verificamos que a primeira depende de \(x\) e é sempre positiva. A segunda parcela é constante. Portanto, o menor valor desta soma é atingido quando \(\displaystyle \left( x+\frac{b}{2a} \right)^2\) é igual a zero, ou seja, quando \(x=-b/2a\). Neste ponto, \(f(x)\) também assume o seu valor mínimo. Concluímos assim que, quando \(a>0\) o menor valor (mínimo da função) assumido por \(f(x)\) é: \(f(-b/2a)=c-(b^2/4a)\). Se \(a<0\), o valor \(f(-b/2a)\) é o maior dos números \(f(x)\) (máximo da função), para qualquer \(x \in \mathbb{R}\). Quando \(a>0\), \(f(x)=ax^2+bx+c\) não assume valor máximo, é assim uma função ilimitada superiormente. Analogamente, quando \(a<0\), \(f(x)\) não assume valor mínimo sendo assim uma função ilimitada inferiormente. |
|
Referências
- 1 LIMA, Elon Lages, CARVALHO Paulo Cezar, WAGNER Eduardo, MORGADO Augusto César, (1997) A Matemática do Ensino Médio - Volume 1, 2ªedição, Coleção do Professor de Matemática, Sociedade Brasileira de Matemática, Rio de Janeiro.
Este artigo já foi visualizado 3977 vezes.



