Lei da entropia

Metáforas com macacos e Shakespeare, ou outras análogas, têm sido utilizadas por vários cientistas como, por exemplo, o biólogo Richard Dawkins² e o astrofísico Fred Hoyle³ no âmbito da seleção natural dos seres vivos. Alguns argumentos de Dawkins basearam-se num programa computacional o qual adaptámos ao presente algoritmo genético. Analisemos agora a ideia que Henry Bent transmitiu¹ com a sua metáfora.

Durante a queda dum objeto a energia potencial inicial vai-se convertendo em energia cinética até que se imobilize no solo. Então, a energia localizada no objeto converte-se em energia térmica que se dispersa no solo, na atmosfera e no próprio objeto. É o exemplo típico de processos irreversíveis, uma vez que não é expetável que, espontaneamente, o objeto se levante do chão retornando ao seu estado inicial. Isto implicaria que a energia térmica, dispersa por diferentes locais, se concentrasse e orientasse sob o objeto, de modo a sustentar o trabalho de ascensão. Estes factos, e tantos outros comprovados experimentalmente, são expressos num dos enunciados da lei da Entropia (2ª lei ou 2º princípio da Termodinâmica): “em processos irreversíveis a entropia do universo aumenta, atingindo o valor máximo no estado de equilíbrio”. Neste caso, o universo termodinâmico é a união do objeto, do solo e da atmosfera constituindo um sistema isolado.

A entropia é uma função do número de microestados realizados pelo universo na sua evolução temporal. Os microestados são identificados pelas posições e velocidades moleculares. As moléculas ocupam os níveis de energia disponíveis dando lugar a distribuições diferentes, cada uma com um determinado número de microestados, mas mantendo a energia total constante porque o universo é um sistema isolado (1ª lei da Termodinâmica). A Termodinâmica Estatística calcula as probabilidades das diferentes distribuições, concluindo que o estado do universo, após um processo irreversível, corresponde à distribuição de maior probabilidade (com o maior número de microestados e dispersão da energia), isto é, o estado de entropia máxima. Esta conclusão confirma a lei da entropia, enunciada pela primeira vez pela Termodinâmica Clássica sem qualquer fundamento estatístico. Então, o evento do objeto ascender, espontaneamente, está em contradição com a lei da entropia porque implica uma diminuição da entropia e dispersão da energia do universo. Além disso, sugeria a ideia (um sonho ainda recorrente) de conceber processos cujo único resultado fosse a conversão total de energia térmica em trabalho que, no caso do objeto, resultaria na conversão total de energia térmica em energia potencial. É claro que uma máquina a vapor converte energia térmica (“calor”) em trabalho, mas não é o único resultado porque parte da energia, proveniente da fonte quente, não é convertida em trabalho pois transita para a fonte fria aumentando a entropia do universo. Em suma, após um processo irreversível nada fica como antes: o universo vai perdendo a capacidade de produzir trabalho pois parte da energia disponível (energia livre) para esse fim degrada-se em energia térmica, a qual não pode converter-se completamente em trabalho.

Todavia, a existência de uma distribuição molecular com probabilidade máxima não descarta as distribuições com probabilidades inferiores que eventualmente conduzam à diminuição e não ao aumento da entropia do universo. Na realidade, as moléculas movem–se incessantemente e nada impede que realizem essas distribuições ao longo do tempo. Há, de facto, uma determinada probabilidade, ainda que praticamente negligenciável, da energia térmica se converter, por si só, completamente em trabalho levando o objeto a ascender repentinamente com a diminuição da entropia do universo. É precisamente a ordem de grandeza desta probabilidade ( \(≃ 10^{−( 10^{23} )}\) ) que Henry Bent comparou com a probabilidade da escrita dos macacos a qual é simples estimar:

Suponhamos uma máquina de escrever com o alfabeto inglês e outros caracteres (pontos, vírgulas, chavetas, espaços em branco, etc.), num total de 95 caracteres, e se pretende que um macaco batendo nas teclas reproduza a frase “To be or not to be? That is the question!”. A probabilidade de obter um determinado carácter ao acaso é \(1/95 ≃ 10^{−2}\), donde a probabilidade da frase, que tem 41 caracteres, ser reproduzida totalmente ao acaso é \(10^{−2\times41}≃ 10^{−82}\), ou seja, cerca de 1 possibilidade entre 10⁸². A obra completa de Shakespeare tem 884421 palavras⁴. A média de caracteres das palavras inglesas é ≈ 5, donde a probabilidade da obra ser reproduzida ao acaso é cerca de 10^−8844210. Por conseguinte, a probabilidade de determinada quantidade energia térmica, 1 cal (4,186 J) por exemplo, se converter espontânea e completamente em energia potencial é, de facto, menor do que a da escrita metafórica dos macacos. Note-se que a ordem de grandeza destas probabilidades significa que a eventual ocorrência dos ditos eventos necessitaria de um tempo muito superior ao da idade do Universo (≈ 14 mil milhões de anos), ou seja, pode concluir-se que ambos os eventos são praticamente impossíveis. Contudo, dado que as probabilidades não são iguais a zero, se for admitido um tempo infinitamente longo não se exclui a hipótese dos macacos executarem (virtualmente, é claro) a tarefa e do Universo retornar ao seu estado inicial. O que é expresso pelo teorema da infinitude referente aos macacos (infinite monkey theorem) e pelo teorema da recorrência de Poincaré acerca do Universo (disponíveis na Internet). Curiosamente, macacos virtuais versus Shakespeare estão atualmente a servir-se de supercomputadores, ao que parece com sucesso (veja-se o link da FIGURA 1). Voltaremos ao tema da entropia mais adiante.

Algoritmos genéticos

Um algoritmo genético é uma técnica de otimização baseada nos princípios evolucionários da seleção natural e da genética. Daqui o seu nome e a sua terminologia: os algoritmos usam populações de objetos (designados cadeias de carateres, cromossomas, genes, etc.), potenciais candidatos à solução de determinado problema. Os cromossomas cruzam-se, sofrem mutações e dão lugar a sucessivas gerações na direção da melhor solução.

Desempenham um papel relevante especialmente em química, bioquímica e biologia para resolver problemas de grande complexidade e quantidade de informação^{5, 6}, a par de outros métodos da inteligência artificial. Questões a que os algoritmos genéticos podem responder são, por exemplo:

• - Como determinar as conformações de energia mínima de proteínas?
• - Quantos isómeros de C₂₆H₅₆O são éteres contendo apenas um anel benzénico?
• - Como otimizar a síntese em fluxo (“flow shop”) de compostos químicos numa unidade industrial?
• - Como simular os efeitos de mutações e cruzamentos dos cromossomas na reprodução e seleção natural dos seres vivos?

A complexidade destes problemas reside no número extremamente elevado de possibilidades a considerar e nas características específicas de cada sistema. As proteínas enrolam-se de forma a encontrar a conformação de energia mínima. Todavia, a conformação que uma determinada proteína adota num organismo vivo pode não ser a do mínimo global, mas o número de mínimos locais é enorme. Os hidrocarbonetos, C_nH_2n+2, por exemplo, têm 5, 75 e > 10⁹ isómeros para n = 6, 10 e 30 respetivamente, donde a ordem de grandeza do número de isómeros para compostos com mais elementos será bastante superior. As sínteses em fluxo de compostos químicos podem realizar-se por diferentes caminhos bem como a reprodução e seleção natural dos seres vivos. É o que se designa “explosão combinatória”.

Contudo, os passos mais elementares dos algoritmos para cada problema são semelhantes. Assim, podem ser compreendidos através de programas simples, como o que apresentamos, que exemplifiquem os conceitos básicos envolvidos no desenvolvimento de algoritmos mais complicados.

Algoritmo monkey business

O ficheiro executável “monkeybusiness.jar”, está acessível em www.casadasciencias.org. Pode correr em Windows, Unix ou Linux desde que o Java Runtime Environment (JRE) esteja atualizado. É conveniente verificar as opções de segurança e privacidade dos computadores (em especial nos Mac). Em geral, para executar o programa basta clicar em “monkeybusiness.jar”, embora alguns sistemas possam requerer a definição de um “path” para o local onde o ficheiro for instalado. Além da interface gráfica, o programa mostra uma janela suplementar com o Resumo/Guia e Exercícios propostos.

Vejamos, sucintamente, os passos essenciais do algoritmo:

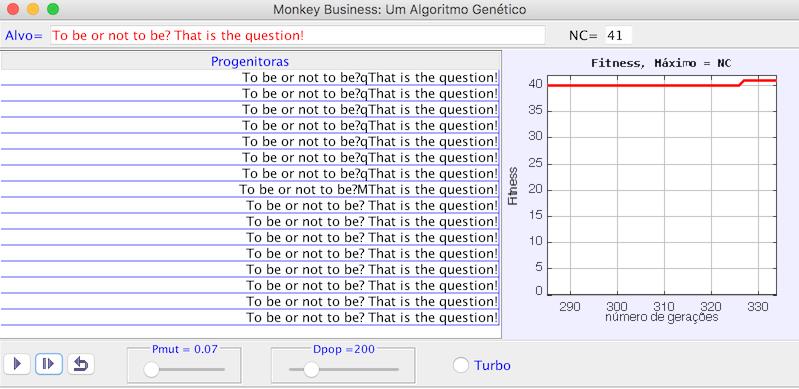
1) A frase-alvo que se pretende reproduzir, “To be or not to be, that is the question!”, já está introduzida. Tem 41 carateres (NC=41); os espaços em branco também contam.

2) Geração aleatória de 41 carateres alfa-numéricos de modo a obter uma população inicial com o número de frases pré-estabelecido, Dpop=200, designado “dimensão da população”.

3) Determinação da qualidade de cada uma das frases da população através da função “Fitness”. Esta função calcula o número de carateres da cada frase que eventualmente coincidam com os da frase-alvo, quer no valor alfa-numérico quer na respetiva posição.

4) Seleção da frase com maior Fitness (“progenitora”).

5) Mutação sucessiva dos carateres da progenitora com uma probalidade pré-definida (Pmut=0.07), gerando um nova população de dimensão Dpop=200.

6) Volta ao passo ao passo 3).

A frase-alvo e os valores de Pmut e Dpop foram pré-estabelecidos, mas podem ser alterados conforme as intruções no Resumo/Guia e Exercícios da janela suplementar.

Porque razão gera o algoritmo genético a frase-alvo após um número relativamente pequeno de gerações? Pois bem, a frase escolhida como progenitora é sempre a de maior Fitness e as mutações são efetuadas com a probabilidade Pmut < 1. Isto é, embora com elementos aleatórios, o processo não é absolutamente ao acaso porque nem todas os caracteres das sucessivas gerações sofrem mutações e a escolha das progenitoras garante a aproximação das sucessivas gerações à frase-alvo. Pelo contrário, se a simulação for executada de modo a que todos os caracteres sejam alterados ao acaso (Pmut =1), então a frase-alvo não será reproduzida, o que traduz a improbabilidade dos macacos realizarem a tarefa.

É evidente uma certa semelhança com a reprodução e a seleção natural dos seres vivos. Neste sentido, no entanto, o algoritmo simula, quando muito, a reprodução assexuada porque em cada geração existe uma única progenitora. Para a reprodução sexuada são necessários dois progenitores e o cruzamento dos respetivos cromossomas, garantindo que os descendentes herdam as caraterísticas dos seus ascendentes. Algoritmos genéticos mais complexos do que o presente incluem cruzamentos. O modo de os efetuar depende das particularidades de cada problema. Um exemplo muito simples dá a ideia básica. Sejam dois progenitores:

A B C D m p x y

F G H J i w o r

Cindindo as cadeias em D e J e trocando as partes terminais, os descendentes são:

A B C D i w o r

F G H J m p x y

Para muitos especialistas parece inequívoco que a seleção natural dos seres vivos, embora com elementos aleatórios, está longe de ser fruto do acaso absoluto^{2, 3}, o que as simulações, em certa medida, também sugerem. Contudo, enquanto o algoritmo presente tem como objetivo (definido por nós antecipadamente) a reprodução de uma única frase-alvo, no caso dos seres vivos o objetivo (propósito) não foi definido por nós e os resultados são multivariados, sendo as questões acerca da origem e natureza do propósito essencialmente filosóficas.

Mas voltemos à entropia. Tanto a geração da frase-alvo como a de seres vivos produzem estruturas organizadas. Se estes fossem os únicos resultados, então a entropia do universo diminuiria, em contradição com a lei da entropia. Contudo, ambos os processos exigem energia para sustentar o trabalho computacional (eletrónico) e biológico, mas parte dessa energia é inevitavelmente convertida em energia térmica (“calor”) que se dispersa pela vizinhança. Assim, o balanço global é o aumento da entropia do universo, a despeito de, localmente, a entropia diminuir, tal como no caso da queda do objeto se uma força contra a gravidade for aplicada para reaver a energia potencial inicial. A propósito, o professor americano Myron Tribus dizia: “A entropia de qualquer sistema pode diminuir à custa de outro corpo. Não há processos que não possam ser revertidos, se aceitarmos uma maior irreversibilidade algures”, ao que um aluno questionou: “Como se pode desmexer um ovo mexido?”. A resposta redentora do professor: “Dei-o a comer à galinha”. Enfim, humor e entropia também se casam!

Inteligência artificial

Desde a década de 1990 que os métodos da inteligência artificial (IA) têm vindo a ser aplicados em química, bioquímica, biologia, medicina e indústrias afins. Em 1995, Cartwright⁵ escreveu: “IA é uma área jovem e largamente inexplorada. Apesar da sua história ser muito curta, o seu potencial é inequívoco: IA será uma parte central do arsenal dos químicos dentro de duas décadas”.

De facto, existem inúmeros problemas de extrema complexidade e quantidades de informação, cujo tratamento pode ser eficientemente realizado através desses métodos que simulam o raciocínio inteligente, os mecanismos genéticos, e a aquisição e manipulação do conhecimento.

O cérebro humano, constituído por uma rede de neurónios massivamente paralela, não funciona sequencialmente. Os neurónios têm, individualmente, um desempenho semelhante, porventura simples, mas dispostos em arquiteturas paralelas possuem a capacidade de processamento simultâneo e integrado, trocando entre eles a informação recebida do exterior ou gerada internamente, manifestando capacidades extraordinárias como os saltos intuitivos, a autoaprendizagem e a auto-reprogramação. Quem faça palavras cruzadas, por exemplo, certamente não procura exaustivamente todas as palavras que conhece e que possam caber no espaço indicado; bastam, por vezes, uma ou duas letras ou palavras para surgir o tal “salto intuitivo”. A aprendizagem requer experiências repetidas, treino e memorização, inevitáveis na tomada de decisões^{7, 8}. A reprogramação é a capacidade de, conforme as circuntâncias, alterar os procedimentos de forma a encontrar alternativas para resolver os problemas. Por outro lado, os seres vivos têm a capacidade de se reproduzir, sujeitos à seleção natural. São, essencialmente, estas capacidades que os métodos de inteligência artificial tentam simular e que os distingue dos métodos mais tradicionais. As redes neuronais artificiais, os algoritmos genéticos e os do crescimento de estruturas celulares, a programação genética e os sistemas-especialistas são exemplos de métodos inteligentes utilizados nas ciências exatas e da vida.

Os algoritmos inteligentes podem incluir, também, a lógica difusa (“fuzzy logic”)^{6, 9}, uma área de notável interesse científico e industrial. Esta lógica generaliza as regras formais de raciocínio estabelecidas por Aristóteles, permitindo tratar inúmeros problemas complexos caraterizados por incertezas intrínsecas. Por exemplo, a resposta a uma questão pode não ser exatamente “sim” ou “não”, mas “talvez” e a cor dum objeto pode não ser exatamente “preto” ou “branco”, mas “cinzento”, existindo dentro destes uma infinidade de tonalidades. Atualmente é vulgar encontrar processadores “fuzzy” em máquinas de lavar roupa e louça, automóveis e ar condicionado. Estes processadores, contrariamente aos digitais (de 0’s e 1’s) têm uma variação contínua entre 0 e 1, conduzindo a controlos suaves com poupanças de energia e água consideráveis.

Já mencionámos algumas questões a propósito dos algoritmos genéticos. Exemplos de outras aplicações são^{5, 6, 10 - 12} :

- O número de moléculas que potencialmente podem atuar como fármacos estima-se ser da ordem de 10⁴⁰. Deste número astronómico de possibilidades, apenas uma infíma fração será eventualmente sintetizada e, desta, somente um número ainda menor será submetido a uma rigorosa avaliação para testes humanos. Qualquer procedimento computacional concebido para este fim deve ser capaz de considerar o número de potenciais fármacos sem efetivamente inspecionar cada uma das estruturas moleculares.

- Previsão dos espetros de ressonância magnética nuclear (RMN) de moléculas ainda não sintetizadas e a determinação das relações quantitativas de estrutura-propriedades moleculares (QSPR).

- Correlações entre a composição química de combustíveis e o seu desempenho, permitindo a previsão das características de combustíveis que ainda tenham de ser formulados no laboratório ou testados no terreno. Ou correlações entre a composição química de vinhos e azeites e a sua qualidade, para o mapeamento classificado das diferentes regiões vinícolas e olivícolas.

- Mapeamento de superfícies de energia potencial (PES) de sistemas heterogéneos em conjugação com métodos quânticos.

- Avaliação de testes e análises médicas com resultados contraditórios e inconclusivos de forma a produzir diagnósticos consistentes.

O algoritmo genético “monkey business” não inclui a maioria das capacidades da inteligência artificial. Todavia, tem os elementos básicos para compreender o objetivo da “programação genética”, a que Cartwright⁶ chamou “Cálice Sagrado” da computação científica. A ideia fundamental é substituir os carateres das cadeias (frases, no nosso caso) por instruções codificadas de forma a gerar programas alternativos, selecionando e executando automaticamente o que melhor se adapte à resolução dum dado problema. A única ação do utilizador é fornecer a descrição do problema. A tarefa do computador é auto-reprogramar-se conforme a informação recebida.

Conclusão

A propósito de uma metáfora analisámos a natureza estatística da lei da entropia, introduzimos um algoritmo genético que reproduz frases e referimos alguns aspetos da inteligência artificial e da sua importância nas ciências exatas e da vida.

Como tudo em ciência, os métodos da inteligência artificial não são “varinha-mágica”, mas é indubitável que contribuem para a resolução de problemas de extrema complexidade como os que referimos. Sublinhe-se, no entanto, que os métodos mais tradicionais não são de somenos importância. Por exemplo, o ajuste dum conjunto de dados experimentais a uma reta ou polinómio pelo método dos mínimos quadrados, que por vezes até pode ser realizado por calculadoras de bolso, é de longe mais eficaz do que um método inteligente. De modo semelhante, embora o cáculo dos níveis de energia de moléculas poliatómicas possa não ser trivial em termos computacionais, os algoritmos convencionais da mecânica quântica são em geral mais eficientes. Em suma, a escolha entre um método tradicional e um método inteligente, ou da conjugação de ambos, depende da natureza do problema que se pretenda resolver.

Qualquer algoritmo é um conjunto de passos elementares para resolver um determinado problema, científico ou não. Uma receita culinária, por exemplo, não é mais do que um algoritmo. Numa fase inicial é conveniente esboçá-lo numa linguagem natural, no nosso caso em português como exemplificámos, pois facilita a sua interpretação. Todavia, para que o computador o compreenda é necessário codificá-lo numa linguagem de programação. O programa apresentado foi codificado em Java. Embora o código não seja aqui listado, pode ser examinado e alterado seguindo as instruções dadas na janela suplementar. A sua compreensão é praticamente imediata, se já se souber uma linguagem de programação (Basic, Python, Fortran, C++, etc.). De contrário, uma leitura atenta das estruturas básicas do Java será suficiente; na Internet existem vários textos didáticos sobre o assunto.

Os algoritmos científicos baseiam-se geralmente em técnicas numéricas avançadas. Não é o caso do programa “monkey business” que está perfeitamente ao nível dos últimos anos do ensino secundário.