Os fósseis são restos ou manifestações da atividade de antigos organismos, preservados habitualmente em rochas. As pistas de pegadas de dinossauros são um exemplo dessa atividade e permitem aferir dados sobre o modo de vida e comportamento desses animais. Consideramos que este contexto seria adequado para o desenvolvimento de uma atividade interdisciplinar, integrando as Ciências Naturais e a Matemática, na qual se partisse de uma pista de pegadas de um terópode para realizar inferências relativa à sua locomoção, como resultado de um processo de modelação matemática.

A fase de preparação foi demorada e implicou um estudo aprofundado do tema, em particular, das características morfológicas dos terópodes e da forma como estas determinam o seu movimento, dos aspetos da dinâmica de locomoção de outros animais e das relações que se podem estabelecer entre elas^1,2. A consulta da literatura da especialidade mostrou que existem dois fatores determinantes para o espaçamento entre as pegadas de uma pista: o comprimento da perna do terópode (dado por uma grandeza designada altura da anca – distância da articulação da anca ao chão, quando em posição de caminhada) e a sua velocidade de deslocação. Como não existem dinossauros vivos nem um registo fóssil que nos permita ter uma noção clara e abrangente da biometria das diferentes espécies de dinossauros, é necessário utilizar modelos matemáticos para obter uma estimativa da altura da anca a partir de alguns elementos conhecidos. Um dos modelos usado pelos paleontólogos, é a fórmula de Thullborn:

H = 3,06.FL^1,14

que calcula a altura da anca H (em cm) de dinossauros terópodes de pequena e média dimensão em função do comprimento da pegada FL (em cm) (FIGURA 1)²:

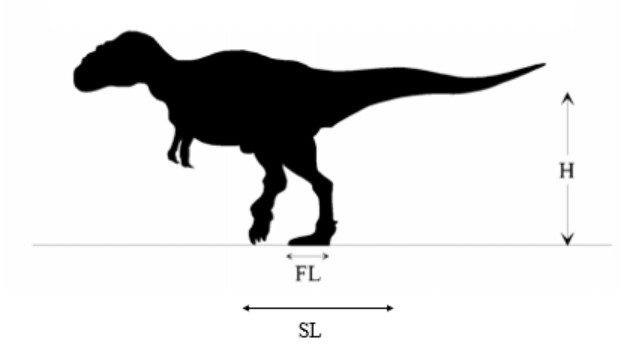
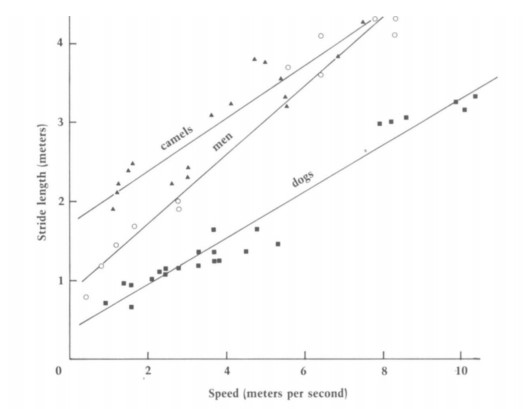
Outra questão a ter em conta é o comprimento da passada (SL), que corresponde, grosso modo, a duas vezes o comprimento do passo. Por um lado, animais com membros posteriores mais compridos produzem passadas maiores do que outros com pernas mais curtas e, por outro lado, à medida que um animal corre mais depressa, as suas pernas descrevem um arco mais longo, pelo que o comprimento da passada tende a ser maior. Na FIGURA 2A podemos observar um diagrama de dispersão onde se correlaciona o comprimento da passada e a velocidade em três espécies distintas, entre elas o ser humano¹. O gráfico mostra que existe uma associação forte entre estas duas variáveis em cada espécie, mas, por outro lado, vemos que o modelo de regressão linear que traduz essa relação varia de espécie para espécie. Por si só, este facto colocaria em causa a resposta a um problema envolvendo uma espécie que, por se encontrar extinta, não nos poderia fornecer os dados necessários à obtenção de um modelo de regressão específico.

Apenas existindo uma regra geral, isto é, um único modelo de regressão que seja válido para diferentes espécies, é que o problema a propor à turma seria passível de ser abordado. Para que se possa comparar a dinâmica de locomoção de animais de diferentes tamanhos e com diferentes tipos de locomoção, teremos de utilizar grandezas relativas, adimensionais, que tenham em conta essas diferenças. Como refere Alexander, partindo do princípio que a locomoção se processa da forma mais eficiente possível, animais movendo-se com igual velocidade adimensional (av) produzirão passadas de comprimento relativo muito semelhante, o que fará com que seja possível comparar diferentes tipos de animais e de diferentes tamanhos. Na FIGURA 2B podemos observar um diagrama de dispersão onde se correlaciona o comprimento relativo da passada e a velocidade adimensional para várias espécies animais, bípedes ou quadrupedes, grandes ou mais pequenas¹.

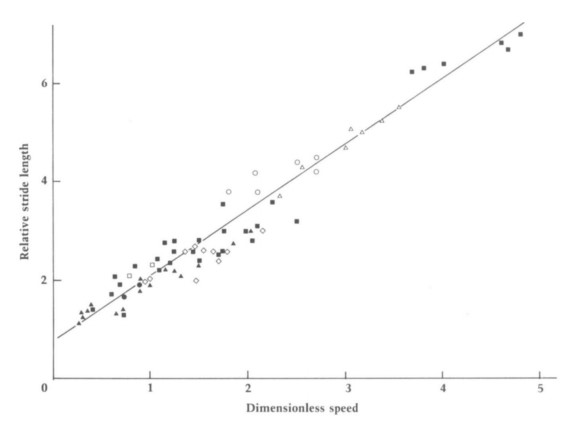
FIGURA 2. A- Diagramas de dispersão das variáveis velocidade (m/s) e comprimento da passada (m) para três espécies distintas; B- diagrama de dispersão para a velocidade adimensional e o comprimento relativo da passada para humanos (○), avestruzes (●), cães (■), elefantes (□), ovelhas (△), camelos (▲) e rinocerontes (◇) ¹.

Da observação do gráfico da FIGURA 2B podemos perceber que, efetivamente, é possível estabelecer um modelo único para relacionar a velocidade com o comprimento da passada, e que isso será feito através do uso de grandezas adimensionais. Para tal, não se deve considerar comprimento da passada (SL) mas antes o comprimento relativo da passada (RSL)¹:

\(RSL=\frac{SL}{H}\)

e em vez da velocidade v, a velocidade adimensional (av)¹:

\(av=\frac{v}{\sqrt{g.H}}\)

(g é a aceleração da gravidade: 9,8 m.s^-2).

A relação entre o comprimento relativo da passada e a velocidade adimensional é ainda mais evidente em animais com o mesmo tipo de locomoção. De facto, o alinhamento das pegadas de dinossauros indica que caminhavam com as patas por baixo do corpo. Isto faz com que a dinâmica de locomoção dos dinossauros possa ser comparável à das aves ou dos mamíferos e não, por exemplo, à dos répteis modernos⁵. No caso particular dos dinossauros terópodes, que são bípedes, essa relação pode ser estabelecida com algumas aves ou com os seres humanos, o que nos dá uma base de trabalho empírica para a implementação de um processo de modelação.

Após este estudo prévio, com recurso a moldes e decalques de pegadas de terópodes elaboradas no FabLab da nossa instituição (FIGURA 3A), simulamos uma pista de pegadas que fosse anatomicamente plausível no espaço exterior (FIGURA 3B e 3C) e interior (FIGURA 3D) da ESES, de modo a salvaguardar que qualquer eventualidade climatérica não colocaria em causa a realização da atividade. O tamanho da pegada correspondia a um animal de dimensões realistas para um terópode do período Jurássico e o comprimento da passada deveria sugerir uma velocidade de deslocação verosímil.

FIGURA 3. Molde de pegada de terópode (A) e construção da pista simulada no exterior (B, C) e no interior da escola (D).

Entretanto, e a partir da adaptação das propostas do Department of Geology of Brooklyn College³ e da National Science Teachers Association⁴, elaboramos um guião da atividade para os estudantes. A proposta didática da atividade seguiu uma estratégia Inquiry⁵, operacionalizada através da realização de tarefas associadas aos momentos do modelo de ensino 6E⁶: Engage, Explore, Explain, Exchange, Elaborate e Evaluate.

Para despertar o interesse das estudantes sobre a temática, o momento de ensino Engage incluiu uma visita de estudo ao museu e a realização de um trabalho de campo na Lourinhã. Posteriormente, noutra aula, além do enquadramento da atividade, as estudantes tomaram contacto com a pista de pegadas, sendo confrontadas com o problema ao qual deveriam dar resposta: A que velocidade se deslocou o dinossauro responsável pela pista?

A segunda parte do guião, relativa ao momento Explore, foi idealizada de modo a orientar a atividade dos vários grupos de trabalho no sentido de i) reconhecerem as grandezas envolvidas na análise da pista de pegadas (FIGURA 4); ii) realizarem medições; iii) obterem uma estimativa para a altura da anca do terópode a partir das medições efetuadas, com recurso a um modelo matemático conhecido; iv) implementarem uma metodologia de recolha de dados relativos à locomoção humana e de determinação, no ser humano, dos mesmos parâmetros recolhidos na pista, o comprimento da passada e altura da anca.

Na pista de pegadas proposta, o comprimento da pegada era 30 cm e o comprimento da passada 360 cm, aproximadamente. Cada grupo, autonomamente, obteve valores sensivelmente iguais a estes, com as discrepâncias decorrentes do maior ou menor cuidado na realização da medição. A altura da anca, grandeza associada ao comprimento da perna, foi determinada recorrendo à fórmula de Thullborn para terópodes de pequena e média dimensão², obtendo-se para um comprimento da pegada de 30 cm, o valor de 147,8 cm.

H = 3,06. 30^1,14 ≈ 147,8

É importante sublinhar que cada grupo trabalhou com as suas medições e com os resultados por si obtidos.

Intercalado com o momento exploratório em curso (Explore), foram incluídos no guião da atividade momentos de explicação (Explain) e de aprofundamento (Elaborate) nos quais as estudantes tomaram contacto com a fundamentação teórica da utilização da locomoção humana como base para a construção do modelo que permitiria dar resposta ao problema colocado. Para ajustar um modelo de regressão linear a um conjunto de dados bivariados referentes ao comprimento relativo da passada e velocidade adimensional, seria importante dispor de um conjunto de dados suficientemente grande e cujos valores fossem diversificados, de modo a evidenciar a correlação entre as variáveis. Assim, foi proposto que fossem recolhidos dados em dois tipos de locomoção distintos, nomeadamente, marcha e corrida. A partir daqui cada grupo de trabalho, constituído por 4 ou 5 estudantes, implementou a seguinte metodologia de recolha de dados (ver FIGURA 5):

• I. Seleção de um elemento do grupo para fornecer dados, percorrendo, primeiro a andar e depois a correr, um trajeto plano em linha reta com 20 m. Medir e registar a altura da anca desse elemento (A).
• II. Acompanhamento do elemento A por um outro, o elemento B, cuja função consistia na contagem e registo do número de passos dados pelo elemento A durante o percurso, tanto a andar como a correr.
• III. Cronometragem pelos restantes elementos (C), e realizada de modo independente, do tempo que o elemento A demorou a percorrer 20 m em cada uma das modalidades de locomoção. O tempo registado pelo grupo seria assim a média das diferentes medições.

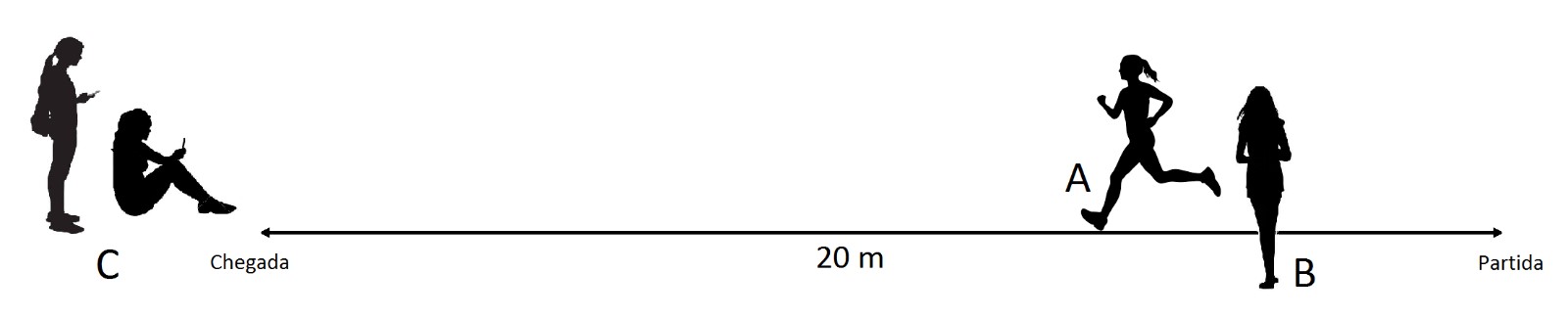
Após a recolha dos dados, os grupos de trabalho determinaram, para cada tipo de locomoção (marcha ou corrida), a velocidade média e o comprimento da passada, passando depois a obter o comprimento relativo da passada e a velocidade adimensional. Com estes valores, preencheram uma tabela contendo os dados e resultados obtidos por todos os grupos (FIGURA 6).

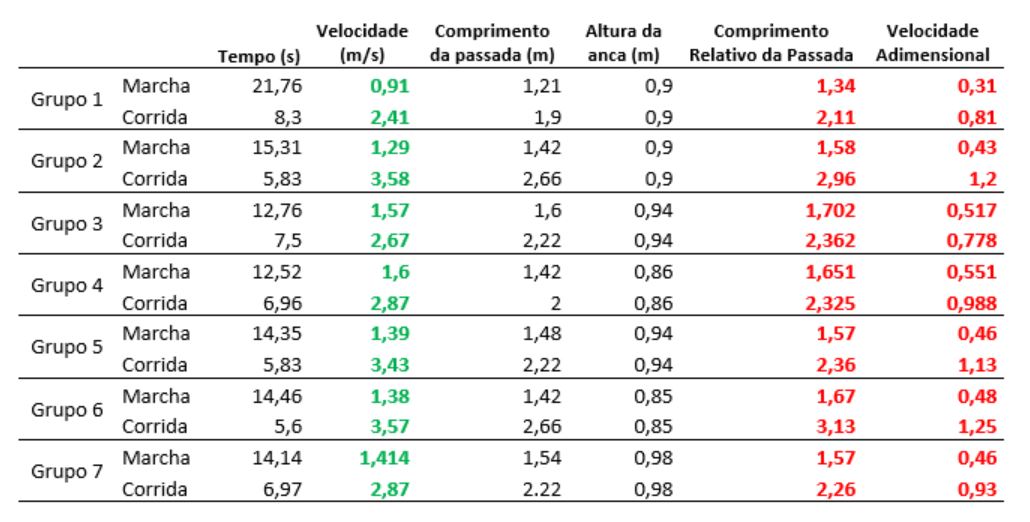
A compilação de todos os dados numa única tabela foi importante na estratégia didática adotada, ao proporcionar um momento de partilha (Exchange). Para além do repositório dos dados obtidos por todos os grupos, a elaboração conjunta desta tabela permitiu às estudantes olhar de formar crítica para o seu trabalho e o das colegas, de analisar os valores obtidos no seu contexto, desenvolver o seu raciocínio numérico e ampliar as suas noções de grandeza e de medida. Esta discussão entre pares, moderada pelos docentes, possibilitou ainda a deteção e correção de erros de registo e de cálculo ocorridos durante o processo.

Partindo desta tabela, os vários grupos construíram o diagrama de dispersão para as variáveis comprimento relativo da passada e velocidade adimensional. A partir daí determinaram a equação da reta de tendência (modelo de regressão linear pelo método dos mínimos quadrados), de modo a relacionar os valores das duas variáveis (FIGURA 7). A obtenção da equação da reta de regressão foi feita recorrendo às ferramentas disponíveis na aplicação informática de folha de cálculo Excel^®.

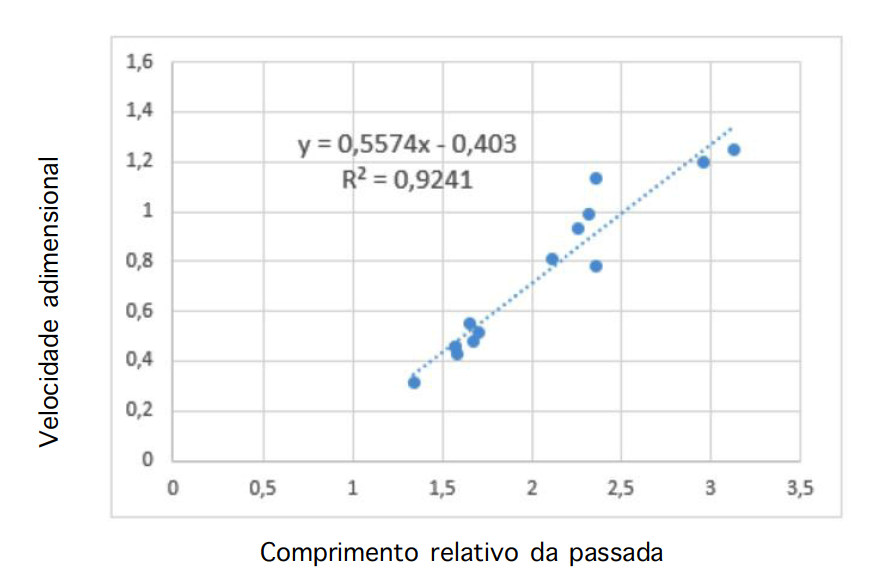
Tomando o modelo encontrado, haveria agora que dar resposta ao problema, realizando os cálculos necessários. Como já vimos anteriormente, para um comprimento da pegada (FL) de 30 cm, a altura da anca estimada (H) de 147,8 cm e o comprimento da passada (SL) de 360 cm, teremos um comprimento relativo da passada de 2,44, aproximadamente.

\(RSL=\frac{SL}{H}=\frac{360}{147,8}≈2,4357\)

sendo este o valor de x a introduzir na equação da reta de regressão. Assim, obtemos uma velocidade adimensional para o dinossauro de, aproximadamente,

\(y=0,5526×2,4357-0,3905≈0,9555\)

Deste modo, de

\(av=\frac{v}{\sqrt{g.H}}\)

vem (convertendo o valor de H para m)

\(0,9555=\frac{v}{\sqrt{9,8\times1,478}}\)

donde resulta que o dinossauro terópode responsável pela pista se deslocaria a uma velocidade aproximada de

\(v = 0,9555 \sqrt{9,8\times1,478} ≈ 3,6365\)

na unidade m. \(s^{-1}\). Nesta fase do trabalho, os professores esclareceram eventuais dúvidas das estudantes relacionadas com o cálculo algébrico, e auxiliaram-nas a dar significado ao valor encontrado, sugerindo a sua conversão para km/h. Este momento gerou alguma discussão de estratégias de resolução em grande grupo (Exchange). Uma das estratégias propostas, consistiu em multiplicar a velocidade inicial pelo fator de conversão 3,6:

\(v=3,6365\) \(m.s^{-1}\) \(=3,6365×3600 \) \(m.h^{-1}\) \(=\frac{3,6365×3600}{1000} \) \(Km.h^{-1}\) \(=3,6365×3,6 \) \(Km.h^{-1}\) \(≈13,09 \) \(Km.h^{-1}\)

resultando em, aproximadamente 13 Km/h.

Cada grupo de trabalho registou as suas produções no guião, o qual foi usado como um dos instrumentos de avaliação da atividade (Evaluate).

Como balanço do trabalho, consideramos que as Ciências da Terra e da Vida proporcionam contextos privilegiados para a resolução de problemas recorrendo à modelação matemática, promovendo assim aprendizagens significativas em ambas as áreas. Da análise das produções dos estudantes e do acompanhamento dos vários grupos no decurso da atividade foi possível constatar, desde logo, que o trabalho de campo na Lourinhã constituiu um elemento fundamental para o enquadramento da atividade desenvolvida, posteriormente, na escola. Este envolvimento promoveu a compreensão acerca do modo como a partir dos registos da atividade de um organismo do passado se podem inferir algumas das suas características e comportamento. A organização da atividade e o seu carácter investigativo, o trabalho em grupo, a interdisciplinaridade e o desenvolvimento de competências digitais foram aspetos que motivaram as estudantes, tendo sido assinalados por estas como mais-valias para a sua formação. As estudantes valorizaram a vertente empírica do trabalho – as observações e as medições de grandezas de diferentes tipos (comprimento, tempo), assim como a construção do modelo matemático a partir de dados reais obtidos de forma direta, como forma de compreender melhor o fenómeno em estudo. Consideramos, assim, que esta atividade interdisciplinar promoveu, nestas futuras professoras/educadoras, o desenvolvimento de um conjunto de competências associadas tanto ao conhecimento do conteúdo, como ao conhecimento didático em Ciências Naturais e Matemática.