Qual é, então, a origem das forças inerciais? Para se perceber, devemos começar por relembrar o 1º Princípio de Newton - um corpo livre (isto é, infinitamente afastado de todos os outros) tem um movimento retilíneo e uniforme. Daqui decorre que se um corpo é livre para um tal observador, então também é livre para qualquer outro observador que, em relação ao primeiro, tenha um movimento uniforme e retilíneo. Tais observadores designam-se por inerciais e são, pois, equivalentes nas suas descrições de corpos livres. O 1º Princípio é, assim, uma afirmação de grande simetria e simplicidade e, na verdade, ele não é alterado pela teoria da relatividade restrita. Por outro lado, é óbvio que um tal corpo não tem aquele movimento para todos os observadores: estrelas distantes rodam em torno da Terra, mas atribuímos aquele movimento à rotação da Terra. Há, assim, observadores inerciais, para quem o ° Princípio é verificado, e observadores não inerciais, para quem o mesmo Princípio não é verificado. E são estes observadores não inerciais que experimentam as forças inerciais exemplificadas acima. Observadores na Terra não são inerciais.

Ora, é, apenas, para os observadores inerciais que se aplica o 2º Princípio de Newton, i.e., um corpo deixa de ser livre e, portanto, deixa de ter movimento uniforme ou retilíneo, por ação de forças originadas em campos. Deste modo, a 2ª lei de Newton escreve-se \(\overrightarrow{a}={\frac{\overrightarrow{F}}{m}}\), i.e., a aceleração do corpo para um observador inercial é a força (conhecida) atuando sobre o corpo, dividida pela massa do corpo.

Considere-se, agora, um observador não inerciai (será notado por O), dotado de um sistema de eixos com versores \(\overrightarrow{i'(t)},\overrightarrow{j'(t)},\overrightarrow{k'(t)}\) que, em geral, dependem do tempo, para o observador inercial, se tal sistema de eixos tiver rotação. Um qualquer corpo terá, para tal observador, uma velocidade e uma aceleração que serão notadas por uma plica. É fácil estabelecer a relação destas grandezas com as mesmas grandezas definidas para o observador inicial. Começando pela posição instantânea do corpo, tem-se:

\(\overrightarrow{r(t)}=\overrightarrow{r'(t)}+\overrightarrow{r_O(t)}\)                     (1)

O 1º membro estabelece a posição do corpo em relação ao observador inercial; no 2º membro, \(\overrightarrow{r_O(t)}\) denota a posição do observador não inercial em relaçao ao inercial; e \(\overrightarrow{r'(t)}=x'(t)\overrightarrow{i'(t)}+y'(t)\overrightarrow{j'(t)}+z'(t)\overrightarrow{k'(t)}\). Note-se, aqui, quer as coordenadas do corpo considerado quer os versores dos eixos usados pelo observador não inercial, dependem do tempo: o corpo move-se em relação a este observador e este pode rodar em relação ao inercial. Se o corpo não se mover em relação aos observador O (não inercial), diremos que está rigidamente ligado a ele.

Derivando a eq. (1) em ordem ao tempo, obtemos a relação entre as velocidades:

\(\overrightarrow{v(t)}=\overrightarrow{v'(t)}+\overrightarrow{\omega(t)}\times \overrightarrow{r'(t)}+\overrightarrow{v_O(t)}\)                     (2)

Aqui, o sinal × denota produto vetorial; e

\(\overrightarrow{v'(t)}=ẋ'(t)\dot{\overrightarrow{i'(t)}}+ẏ'(t)\dot{\overrightarrow{j'(t)}}+ż'(t)\dot{\overrightarrow{k'(t)}}\)

é a velocidade do corpo em relação ao observador não inercial (o ponto significa derivada em ordem ao tempo); \(\overrightarrow{\omega(t)}\) é a velocidade de rotação instantânea do referencial não inercial (em relação ao inercial), sendo definida pelas equações:

\(\frac{d}{dt}\overrightarrow{i'(t)}=\overrightarrow{\omega(t)}\times\overrightarrow{i'(t)}\)

\(\frac{d}{dt}\overrightarrow{j'(t)}=\overrightarrow{\omega(t)}\times\overrightarrow{j'(t)}\)

\(\frac{d}{dt}\overrightarrow{k'(t)}=\overrightarrow{\omega(t)}\times\overrightarrow{k'(t)}\)

Tal resulta de \(\overrightarrow{i'(t)},\overrightarrow{j'(t)},\overrightarrow{k'(t)}\) serem versores, pelo que as suas diferenciais são perpendiculares aos respetivos versores. É óbvio que se os eixos do observador O não rodarem, então os seus versores serão independentes do tempo e \(\overrightarrow{\omega(t)}\)= 0. Nesta caso, a eq. (2) reduz-se à lei de adição de velocidades de Galileu. Finalmente, \(\overrightarrow{v_o(t)}\) é a velocidade do observador não inercial (a origem do seu sistema de eixos) em relação ao observador inercial. Coletivamente, a soma \(\overrightarrow{\omega(t)}\times\overrightarrow{r'(t)}+\overrightarrow{v_o(t)}\) é designada por velocidade de transporte - seria a velocidade do corpo se rigidamente ligado ao observador, pelo que é a expressão da velocidade de um ponto genérico de um sólido rígido.

Uma nova derivação, em ordem ao tempo, da eq. (2) conduz-nos à relação entre as acelerações:

\(\overrightarrow{a(t)}=\overrightarrow{a'(t)}+2\overrightarrow{\omega(t)} \times \overrightarrow{v'(t)}+\overrightarrow{\omega(t)}\times (\overrightarrow{\omega(t)}\times\overrightarrow{r'(t)})+\overrightarrow{ \dot{ {\overrightarrow{\omega} }(t)} }\times\overrightarrow{r'(t)}+\overrightarrow{a_O(t)}\)                     (3)

onde:

\(\overrightarrow{a'(t)}\)á a aceleração do corpo em relação ao observador O (não inercial);

\(2\overrightarrow{\omega(t)} \times \overrightarrow{v'(t)}\) é designada por aceleração de Coriolis - só existe se o corpo se mover, em relação a O, e o sistema de eixos deste observador tiver rotação em relação ao observador inercial;

\((\overrightarrow{\omega(t)}\times\overrightarrow{r'(t)})\) é a aceleração centrípeta, reduzindo-se a \( -\omega(t)^2\overrightarrow{r'_p(t)} \), \( \overrightarrow{r'_p(t)}\) sendo a componente de \(\overrightarrow{r'(t)}\) perpendicular a ω(t), i.e., ao eixo de rotação;

\(\overrightarrow{a_O(t)}\)é a aceleração do observador não inercial O em relação ao inercial.

Coletivamente, a soma \( \overrightarrow{\omega(t)}\times (\overrightarrow{\omega(t)}\times\overrightarrow{r'(t)})+\overrightarrow{\dot{ {\overrightarrow{\omega} }(t)}}\times\overrightarrow{r'(t)}+\overrightarrow{a_O(t)}\) é designada por aceleração de transporte - seria a aceleração do corpo se rigidamente ligado ao observador e, portanto, será a aceleração de um ponto genérico de um sólido.

Podemos, agora, regressar à 2ª lei de Newton, substituindo, no 1º membro, a aceleração \(\overrightarrow{a(t)}\) pela expressão obtida, eq. (3). Resolvendo em ordem a \(\overrightarrow{a'(t)}\), obtemos:

\(\overrightarrow{a'(t)}=\frac{\overrightarrow{F}}{m}-2\overrightarrow{\omega(t)}\times \overrightarrow{v'(t)}-\overrightarrow{\omega(t)}\times(\overrightarrow{\omega(t)} \times\overrightarrow{r'(t)})-\overrightarrow{\dot{ {\overrightarrow{\omega} }(t)}}\times\overrightarrow{r'(t)}-\overrightarrow{a_O(t)}\)                     (4)

Mas agora, olhando para esta equação, podemos reinterpreta-lo como uma 2ª lei de Newton na qual, para além das forças \(\overrightarrow{F}\), surgem devidas aos campos, surgem novas forças originadas por o observador O não ser inercial. Tais forças são coletivamente designadas por forças fictícias ou, preferencialmente, forças de inércia \(\overrightarrow{Fi}\):

\(\overrightarrow{Fi}=-m\left[\overrightarrow{2\omega(t)}\times\overrightarrow{v'(t)}+\overrightarrow{\omega(t)} \times(\overrightarrow{\omega(t)}\times\overrightarrow{r'(t)})+\overrightarrow{ \dot{ {\overrightarrow{\omega} }(t)}}\times\overrightarrow{r'(t)}+\overrightarrow{a_O(t)}\right]\)                     (5)

No 2º membro, o 1º termo é a força de Coriolis. Os outros três termos são coletivamente designados for forças de transporte, reconhecendo-se a força centrífuga no 2º termo. Para aplicações na Terra, e para escalas de tempo inferiores a vários milhares de anos (período de precessão do eixo da Terra), o 3º termo é desprezável. Assim, se na força \(\overrightarrow{F}\) for considerada, separadamente, a atração gravitacional da Terra, m\(\overrightarrow{G}\), como se esta estivesse parada, então esta contribuição adicionada aos 3º e 4º termos na eq. (5), escreve-se na forma mais conhecida, i.e., \(m\overrightarrow{g}\), onde, portanto, \(\overrightarrow{g}\) leva em conta não só a atração gravitacional como o efeito da força centrífuga, originando, assim, a variação da aceleração da gravidade com a latitude.

Note-se que as forças de inércia são proporcionais à massa, tal como o peso, e, por isso, são modernamente chamadas por forças gravíticas, designação que se entenderá melhor quando for discutida a teoria da relatividade geral.

Um exemplo simples: suponha-se que se larga um corpo do alto da torre dos Clérigos (altura h=70m). Considere-se o seguinte sistema de eixos: o eixo z tem a direção e sentido contrário à vertical do lugar \(\overrightarrow{(g)}\) que se pode determinar com um fio de prumo; o eixo x é tangente ao meridiano e aponta para Sul; e o eixo y é tangente ao paralelo, apontando para Este. Se se ignorar a força de Coriolis, um corpo largado livremente cai com movimento uniformemente acelerado \(z=h -\frac{1}{2}g t^2\) e, portanto, a sua velocidade, em qualquer instante, é: \(v_z = - gt\).

Sendo λ ≈ 45° a latitude do lugar, o vetor rotação instantanea da Terra, com a direção e sentido do eixo da Terra e grandeza \(\omega \approx \frac{2\pi}{24*3600}s^{-1}\), faz um ângulo \(\frac{\pi}{2}\)-λ com o eixo z. Assim, a força de Coriolis tem, nesta 1ª aproximação, a direção e sentido do eixo y, i.e., aponta para Este, resultando:

\(\frac{d^2}{dt^2}y=2\omega \cos\)λ gt

Uma 1ª integração dá-nos a velocidade para Este (lembrando que o corpo é abandonado com velocidade nula):

\(\frac{d}{dt}y=\omega \cos\)λ gt²

E nova integração dá o desvio para Este:

\(y=\frac{1}{3}\omega \cos\)λ gt³

Assim, para os valores numéricos indicados, quando o corpo atinge o solo, t= \(\sqrt{\frac{2h}{g}}\)≈ 3.7 s, o seu desvio para Este foi y ≈ 9 mm.

Para maiores alturas de queda, o cálculo exato revela que a trajetória do grave é helicoidal.

Este exemplo mostra a grande vantagem de se ter usado um referencial não inercial (a Terra) porque é neste referencial que a experiência é executada e os seus resultados são reportados. Nada impede que a análise deste mesmo problema seja feita a partir do um referencial inercial, por exemplo, por um astronauta imóvel em relação ao Sol e longe da Terra. Como vê o astronauta o movimento do mesmo corpo largado do alto da torre? Para ele, a partir do momento em que é largado, o corpo fica apenas submetido à força gravítica da Terra determinada unicamente pela massa da Terra, não importando que o planeta esteja a rodar ou não - a força é m\(\overrightarrow{g}\). Mas, agora, o corpo está animado de uma velocidade inicial, a velocidade do ponto no alto da torre de onde ele foi largado. Com estes dados, o astronauta pode calcular a trajetória balística do corpo e pode, assim, determinar onde ele irá chocar junto à base da torre, tendo, para isso, que levar em conta que a Terra rodou enquanto o corpo caía. Percebe­ se que o cálculo seria bem mais elaborado, sendo, contudo fácil perceber por que o corpo atinge o chão a leste da vertical passando pelo alto da torre. De facto, quando o corpo é largado, a sua velocidade inicial é a velocidade da Terra naquela posição inicial, i.e., tangente ao paralelo passando pelo alto da torre. Esta velocidade é ligeiramente maior do que a velocidade da base da torre porque o alto da torre está mais afastado do eixo de rotação da Terra. Além disso, uma vez largado, o corpo só está submetido à força de gravidade, dirigida para o centro da Terra (suposta homogénea, para simplificar). Logo, não é alterada aquela componente da velocidade tangente ao paralelo. Assim quando atinge o solo, o corpo deslocou-se mais, na direção e sentido do paralelo, do que a base da torre - o ponto de impacto situa-se, pois, a leste da base da torre.

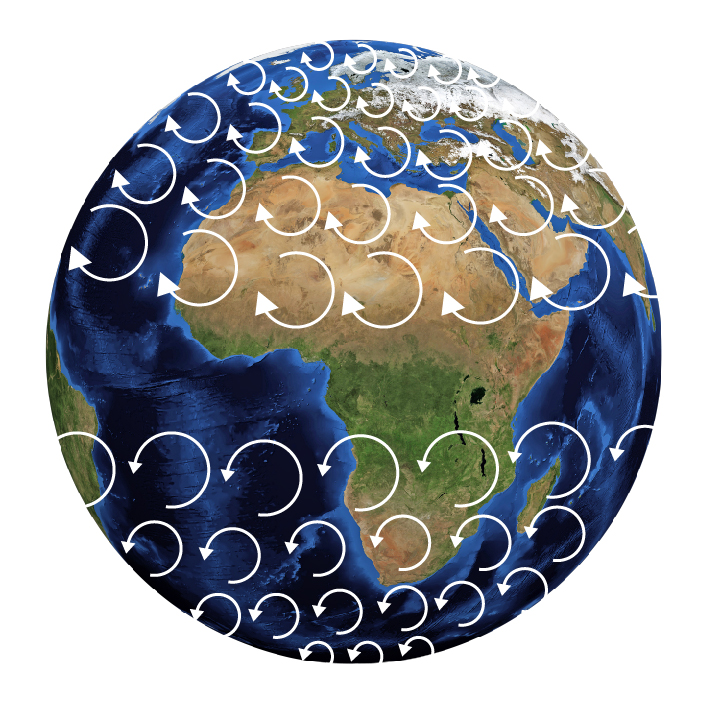
	Muitos outros exemplos podem ser interpretados recorrendo às forças de inércia. A direção dominante dos ventos globais pode se explicada qualitativamente. Não houvesse rotação da Terra, os ventos globais soprariam dos pólos (mais frios, maior pressão) para o equador (mais quente, menor pressão). Mas a Terra roda - a força de Coriolis altera este movimento, como mostra a figura.

Se a Terra não rodasse, um pêndulo simples oscilaria sempre no mesmo plano (designado por plano invariante). Mas a Terra roda fazendo aparecer, para os seus habitantes, a força de Coriolis, perpendicular à velocidade e, portanto, obrigando o plano de oscilação a rodar. É o pêndulo de Foucault, um método simples de exibir a rotação da Terra. O desenvolvimento mais detalhado deste interessante movimento não cabe aqui, mas é fácil percebe-lo, qualitativamente, em duas situações limites. Imagine-se o pêndulo num dos pólos geográficos. Aí, o seu plano de oscilação é invariante para o astronauta atrás referido e, portanto, executa uma rotação completa em um dia para o observador terrestre. Por outro lado, se o pêndulo for colocado a oscilar no Equador, o seu plano de oscilação é arrastado pelo movimento da Terra, pelo que permanece invariante para um observador terrestre. Intui-se, deste modo, que a amplitude de oscilação do plano do pêndulo dá informações sobre a latitude do lugar.

Um outro exemplo é o girocompasso de Foucault, em tempos muito usado em navios. Trata-se de um cilindro maciço, suspenso pelo seu centro de gravidade (suspensão Cardan) e posto a girar por um motor que mantém uniforme a velocidade de rotação. A força de Coriolis tem resultante nula, mas não é nulo o seu momento resultante, pelo que o momento cinético do cilindro não é mais constante, o que origina uma oscilação do seu eixo em torno da direção Norte. De novo, a análise detalhada deste comportamento é deixada para outro artigo.

A explicação qualitativa das marés é um outro exemplo interessante. Comecemos por ignorar o Sol e a rotação da Terra. Nestas condições, a superfície livre dos oceanos, que podem ser considerados em equilíbrio, seria esférica, coincidente com uma superfície isopotencial gravítico da Terra. Com a Terra em rotação, há que introduzir o efeito da força centrífuga, também ela derivada de um potencial com simetria cilíndrica (o eixo do cilindro é o eixo da Terra). Assim, o potencial total, soma dos anteriores, assemelhar-se-ia a uma esfera ligeiramente alongada no equador. Qual o efeito do Sol? Se, numa primeira aproximação, se considerar que a força gravítica do Sol é uniforme (em grandeza e intensidade), aquela superfície apenas seria ligeiramente deslocada, mas não deformada, em relação à parte sólida do planeta. Mas o Sol está a distância finita da Terra: a sua força de gravidade não é uniforme, sendo ligeiramente maior na parte dos oceanos voltada para o Sol e ligeiramente menor na parte dos mesmos oceanos mais afastada do Sol. Assim, a superfície livre dos oceanos deforma-se (em relação à forma quase esférica inicial), ficando mais alongada nas regiões mais próximas do Sol, que exerce maior atração, e também nas mais afastadas porque à menor atração do Sol se sobrepõe a força centrífuga. Imaginando o Sol a rodar em torno da Terra ( é isso que vê um observador terrestre!), haverá marés cheias aproximadamente separadas por 12 horas. A não uniformidade do campo gravítico (do Sol, neste caso) é responsável por estas forças de maré. Numa primeira aproximação, bastante válida para o Sol, essa força é determinada pela derivada da intensidade do campo gravítico solar em ordem à distância ao centro da Terra, isto é, proporcionais ao inverso do cubo da distância. E este resultado mostra a importância da Lua nas marés: a força gravítica exercida pela Lua sobre a Terra é cerca de 5 milésimas da força exercida pelo Sol; mas as respetivas forças de maré são praticamente iguais. A periodicidade das marés é estabelecida quer pelo Sol quer pela Lua.

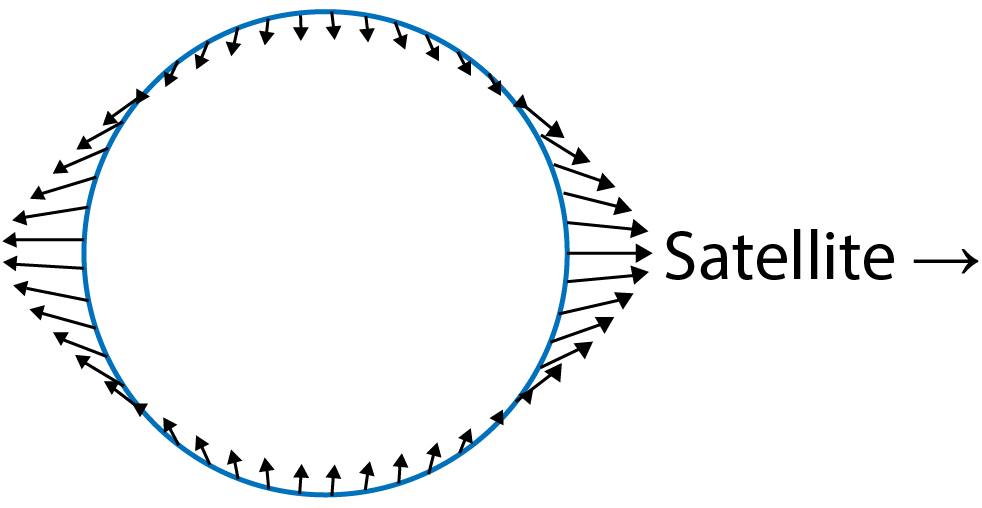
Por último, uma pergunta que o leitor certamente se colocou: existe algum observador inercial?

A resposta poderá ser surpreendente: um observador em queda livre na Terra é, para curtos tempos de queda e para curtas distâncias percorridas, um observador inercial. Designemo-lo por I e designemos por O um outro observador na Terra. Para este, I cai com movimento acelerado devido à atração da Terra. Imaginemos, agora, que I larga uma bola - ela cai, para O, com a mesma aceleração que I e, portanto, para I a bola estará em repouso. Imaginemos que I dá um impulso à bola; para O a aceleração da bola é igual à aceleração de I (enquanto a bola permanecer nas imediações de I). Então, para I, a bola não tem qualquer aceleração, afastando-se com movimento uniforme e retilíneo - para I a bola é um corpo livre que verifica o 1º Princípio e, portanto, ele é um observador inercial. Mas porque foi necessário referir curtos tempos e curtas distâncias? Porque o campo gravítico terrestre não é uniforme, sujeitando I às forças de maré. Tal observador pode verificar isso se largar, em repouso, quatro bolas definindo vértices de um quadrado vertical. Devido às forças de maré, o quadrado deforma-se (enquanto cai com I): o lado inferior, mais próximo da Terra, diminui o comprimento, porque todas as bolas seguem linhas de força do campo gravítico terrestre e estas confluem para o centro da Terra; e os lados laterais esticam, pelo mesmo motivo. O quadrado vai deformando num trapézio.