Se representarmos por (x,y)={ ( x_i,y_i ) }, com i = 1,...,n, uma amostra de dados bivariados, a covariância amostral entre as variáveis x e y é dada pela seguinte expressão:

$${\rm{Cov}}\left( { {\rm{x }},{\rm{y}}} \right) = \frac{ {\rm{1} } }{ { {\rm{n - 1} } } }\sum\limits_{ {\rm{i} } = {\rm{1}}}^{\rm{n}} { {\rm{(} }{ {\rm{x} }_{\rm{i}}}{\rm{ - \bar x)(} } { {\rm{y} }_{\rm{i} } }{\rm{ - \bar y)}}} {\rm{,\quad \quad onde \quad \quad \bar x }} = {\rm{ }}\frac{ {\rm{1} } } { {\rm{n} }}\sum\limits_{ {\rm{i} } = {\rm{1}}}^{\rm{n}} { { {\rm{x} }_{\rm{i}}}} {\rm{ \quad \quad e \quad \quad \bar y } } = {\rm{ }}\frac{ {\rm{1} } } { {\rm{n} } }\sum\limits_{ {\rm{i} } = {\rm{1}}}^{\rm{n}} { { {\rm{y} }_{\rm{i} } } }$$

Uma associação linear entre os x’s e os y’s, do mesmo sentido, isto é, quando a valores grandes (pequenos) de x correspondem, de um modo geral, valores grandes (pequenos) de y, faz com que predominem as parcelas positivas na expressão da covariância, pois quando $(x_{i}-\bar{x})>0\quad(<0)$ , tende a ser $(y_{i}-\bar{y})>0 \quad(<0)$. Então a covariância vem positiva. Geometricamente, tem-se:

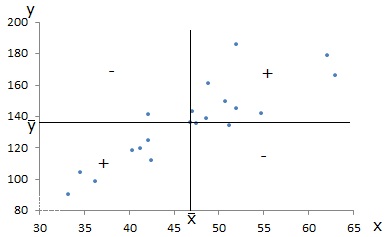
Uma associação linear entre os x’s e os y’s, de sentido contrário, isto é, quando a valores grandes (pequenos) de x correspondem, de um modo geral, valores pequenos (grandes) de y, faz com que predominem as parcelas negativas na expressão da covariância, pois quando $(x_{i}-\bar{x})>0\quad(<0)$, tende a ser $(y_{i}-\bar{y})>0 \quad(<0)$. Então a covariância vem negativa. Geometricamente, tem-se:

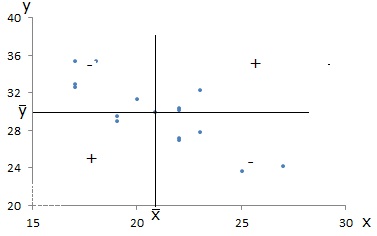
Se não se verificar uma associação linear entre as variáveis, então nem predominam as parcelas positivas, nem as negativas, obtendo-se para a covariância um valor próximo de 0. Geometricamente tem-se:

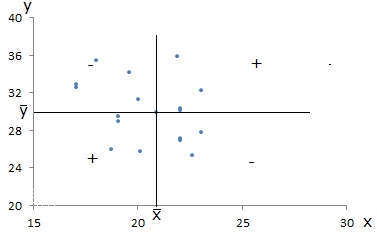
A covariância é uma medida que tem o inconveniente de depender das unidades com que se apresentam os elementos da amostra, pelo que não é normalmente usada. Em sua substituição utiliza-se o coeficiente de correlação amostral, que não depende das unidades utilizadas.