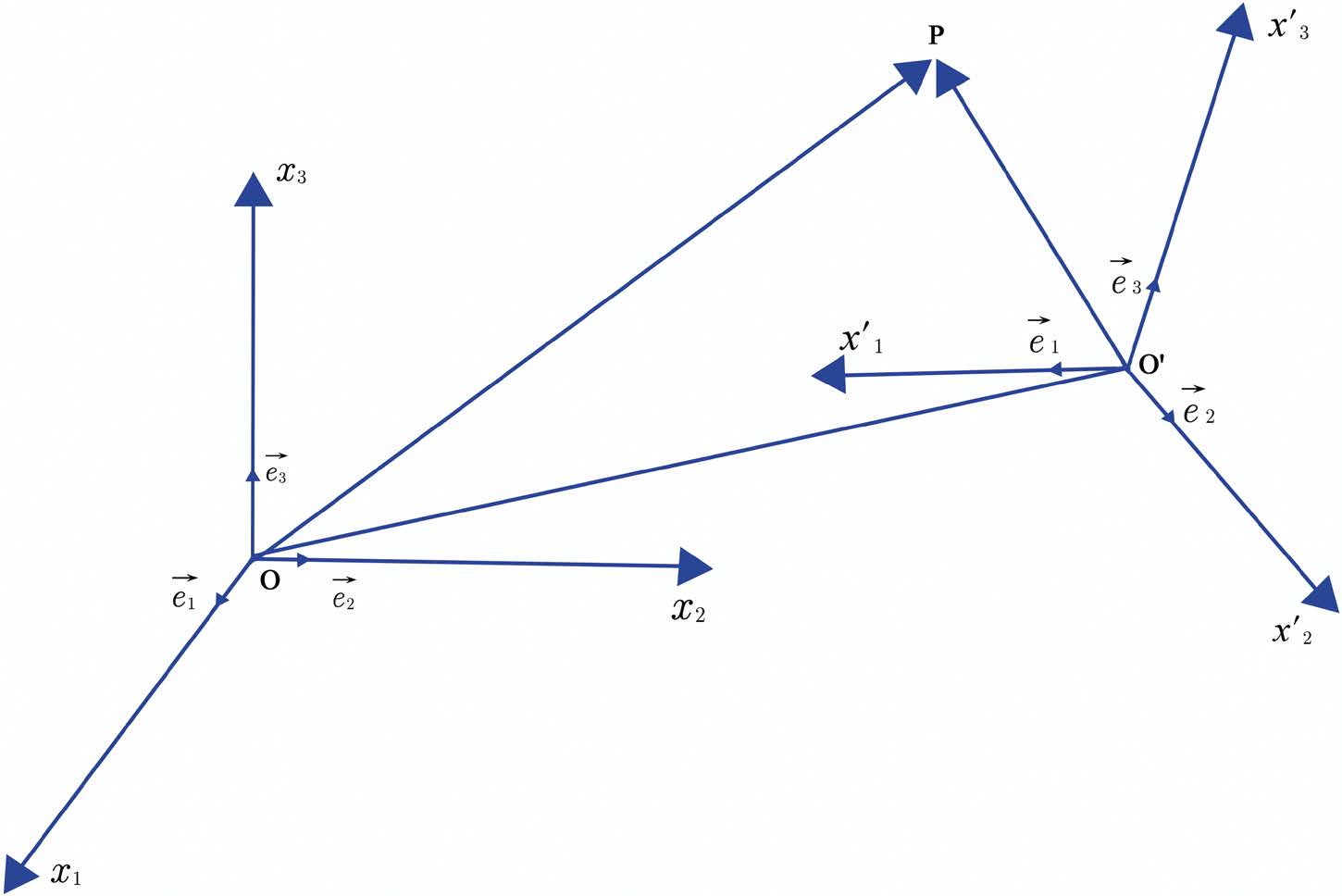
A figura mostra os dois sistemas de eixos: para cada observador, os três eixos são ortogonais entre si e, em cada eixo, é definida uma uma unidade de comprimento, comum não só aos três eixos de um observador como aos três eixos do outro observador. Tal justifica o adjectivo “ortonormado” atrás utilizado. Note-se que cada eixo se prolonga, como linha recta, indefinidamente e que, em cada um, distâncias, a partir da respetiva origem, são afetadas do sinal (+) nos sentidos indicados pelas setas e do sinal (-) nos sentidos opostos. É, assim, muito conveniente associar, com cada eixo, um vetor unitário (versor) com origem na origem do referencial, apontando no sentido positivo do eixo e de tamanho unitário. Deste modo, em cada referencial fica associada uma base (\(\overrightarrow{e_1},\overrightarrow{e_2},\overrightarrow{e_3}\)) que permite univocamente definir, para cada observador, a posição de qualquer ponto no espaço.

Exigiremos, adicionalmente, que os dois sistemas de eixos tenham a mesma orientação. Isso significa o seguinte: se imaginarmos que as origens se sobrepõem (O ≡ O’) e alinharmos \(x’_1\) com \(x_1\) e \(x’_2\) com \(x_2\), fazendo coincidir as respetivas partes positivas, então não só \(x’_3\) alinha com \(x_3\) como também coincidem as respetivas partes positivas. Se, pelo contrário, a parte positiva de \(x’_3\) coincide com a parte negativa de \(x_3\), diremos que os referenciais têm orientações inversas. Por último, designaremos um sistema de eixos por direto se um saca-rolhas progredir segundo a parte positiva de \(x_3\) quando roda (de 90°) da parte positiva de \(x_1\) para a parte positiva de \(x_2\). Se aquela progressão se der para a parte negativa de \(x_3\), diremos que o sistema de eixos é inverso. É óbvio que os dois referenciais da figura são ambos diretos, tendo, pois, a mesma orientação.

Duas notas:

1ª - É muito comum usar-se a notação (\(x,y,z\)) para os eixos, nomeadamente, \(x\equiv x_1, y\equiv x_2, z \equiv x_3\). É completamente arbitrário usar uma ou outra notação mas, como veremos, há grandes vantagens em utilizar a notação mais simétrica (\(x_1, x_2, x_3\)) que será aqui adotada.

2ª - É óbvio que a descrição de uma grandeza física é independente das convenções atrás utilizadas, nomeadamente, a tri-rectangularidade, normalização e orientação dos eixos. E é possível apresentar uma descrição mais geral, liberta destes constrangimentos e desejável para diversos fins, mas que aqui não cabe fazer.

Regressando à figura, vemos que o mesmo ponto \(P\) tem coordenadas (\(x_1, x_2, x_3\)) para o observador \(O\), e (\(x'_1, x'_2, x'_3\)) para o observador \(O’\). A mesma figura mostra a relação:

\(\overrightarrow{OP}=\overrightarrow{OO'}+\overrightarrow{O'P}\)            (1)

sendo, então:

\(\overrightarrow{OP}=x_1\overrightarrow{e}_1+x_2\overrightarrow{e}_2+x_3\overrightarrow{e}_3\equiv x_i\overrightarrow{e}_i\)            (2)

\(\overrightarrow{O'P}=x'_1{\overrightarrow{e}'}_1+x'_2\overrightarrow{e}'_2+x'_3\overrightarrow{e}'_3\equiv x'_i\overrightarrow{e}'_i\)

Aqui, as últimas igualdades mostram já a vantagem da notação simétrica: as duas somas são substituídas por uma notação mais compacta onde o índice repetido indica uma soma (sobre os valores desse índice). O índice repetido é designado por índice mudo e pode ser representado por qualquer outra letra, desde que não haja ambiguidades.

Nas eqs.(2), os três versores são unitários e ortogonais entre si, condições que se resumem na seguinte expressão:

\(\overrightarrow{e}_i\cdot\overrightarrow{e}_j=\delta_{ij} \ \ \ \ \ \ \ \ i,j=1,2,3\)            (3)

onde o ponto indica produto escalar e \(\delta_{ij}\) é o símbolo de Kronecker:

\(\delta_{ij}=\begin{cases}1 & se \ i = j\\0 & se \ i \neq j\end{cases}\)

O mesmo se passa, evidentemente, com os versores \(x'_1, x'_2, x'_3\) do outro observador:

\(\overrightarrow{e}'_i\cdot\overrightarrow{e}'_j=\delta_{ij} \ \ \ \ \ \ \ \ i,j=1,2,3\)           (4)

Regressando a (1), designemos por (\(x_1, x_2, x_3\)) as coordenadas (para o observador O) do ponto O’, i.e.,

\(\overrightarrow{OO'}=x_i\overrightarrow{e}_i\)

Deste modo, a eq. (1) escreve-se:

\(x_i\overrightarrow{e}_i=X_i\overrightarrow{e}_i+ x'_i\overrightarrow{e}'_i\)            (5)

Ora, sendo o espaço tridimensional, as duas bases de representação utilizadas não são independentes. Assim, por exemplo, os versores \(\overrightarrow{e}'_1,\overrightarrow{e}'_2,\overrightarrow{e}'_3\) devem escrever-se como combinações lineares de \(\overrightarrow{e}_1,\overrightarrow{e}_2,\overrightarrow{e}_3\):

\(\overrightarrow{e}'_i=M_{ij}\ \overrightarrow{e}_j\)            (6)

A matriz \([M]\) estabelece a relação entre as duas bases de representação e é fácil deduzir o significado dos seus elementos. Com efeito, usando as eqs. (3) e (5), obtem-se:

\(\overrightarrow{e}'_i\cdot \overrightarrow{e}_k=M_{ij}\ \overrightarrow{e}_j\cdot\overrightarrow{e}_k=M_{ij}~\delta_{jk}=M_{ik}\)            (7)

Usando a definição de produto escalar, tem-se:

\(M_{ik}=\mid\overrightarrow{e}'_i\mid \ \mid\overrightarrow{e}_k\mid \cos (\overrightarrow{e}'_i, \overrightarrow{e}_k)=\cos(\overrightarrow{e}'_i, \overrightarrow{e}_k)\)

Isto é, \(M_{ik}\) é o cosseno do ângulo formado pelas partes positivas dos eixos \(x'_i\) e \(x_k\), o que justifica a designação de cossenos diretores para os elementos da matriz \([M]\). Deve notar-se que estes nove elementos não são independentes; com efeito, usando as eqs. (4) e (6), tem se:

\(\overrightarrow{e}'_i\cdot\overrightarrow{e}'_j=\delta_{ij}=M_{ik}\ \overrightarrow{e}_k \cdot M_{jn} \ \overrightarrow{e}_n=M_{ik}M_{jn} \overrightarrow{e}_k\cdot\ \overrightarrow{e}_n=M_{ik}M_{jn}\delta_{kn}=M_{ik}M_{jk}\)

onde se invocou a eq. (3). Assim:

\(M_{ik}M_{jk}=\delta_{ij}\)            (8)

ou, em termos matriciais:

\(\left[M\right]\left[M\right]^T=1\)

Aqui, o sobrescrito \(T\) significa matriz transporta e 1 é a matriz unidade. Estas matrizes dizem se ortogonais, sendo agora fácil obter a relação inversa da eq. (6):

\(\left[M^{-1}\right]_{ki}\overrightarrow{e}'_i=\left[M^{T}\right]_{ki}\overrightarrow{e}'_i=M_{ik}\ \overrightarrow{e}'_i=\left[M^{-1}\right]_{ki}\left[M\right]_{ij}\ \overrightarrow{e}_j=\overrightarrow{e}_k\)            (9)

Como o determinante de um produto de matrizes é o produto dos respetivos determinantes, e como o determinante de qualquer matriz é igual ao determinante da sua transposta, segue-se que:

\(\det\left[M\right]=\pm \ 1\)

Este resultado mostra como distinguir algebricamente a orientação de dois referenciais cartesianos: se \(\det\left[M\right]=1\), têm a mesma orientação e se \(\det\left[M\right]=-1\), têm orientações inversas.

Exemplos (considera-se \(O ≡ O’\), embora seja irrelevante porque a matriz \([M]\) não depende das origens escolhidas para os eixos)

a) O sistema de eixos (\(x'_1, x'_2, x'_3\)) obtem-se de (\(x_1, x_2, x_3\)) rodando, no sentido direto, de um ângulo \(ϕ\) em torno do eixo comum \(x_3\equiv x'_3\):

\(\left[M\right]=\begin{bmatrix}\cos\phi & sen\phi & 0 \\-sen\phi & \cos\phi & 0 \\0 & 0 & 1 \end{bmatrix}\rightarrow \det\left[M\right]=1\)

b) O sistema de eixos (\(x'_1, x'_2, x'_3\)) obtem-se de (\(x_1, x_2, x_3\)) por reflexão especular no plano (\(x_2, x_3\)):

\(\left[M\right]=\begin{bmatrix}-1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 1 \end{bmatrix}\rightarrow \det\left[M\right]=-1\)

Regressando à eq. (1), os resultados obtidos permitem escrever:

\(x_i\overrightarrow{e}_i=X_i\overrightarrow{e}_i + x'_i\overrightarrow{e}'_{i}=X_i\overrightarrow{e}_i + x'_i \ M_{ij}\overrightarrow{e}_j\)

No último termo, podemos trocar \(i\) com \(j\) porque são ambos índices mudos (apenas indicam somas!). Com o resultado assim obtido e dada a independência linear dos vetores da base, tem-se, finalmente:

\(x_i=X_i+M_{ji}x'_j\)            (10)

Escalares

Qualquer função que tenha o mesmo valor para os dois observadores é um escalar. São disso exemplos conhecidos a temperatura (FIGURA 2), a massa ou carga elétrica de um corpo, o volume de um domínio, a área de uma superfície ou o comprimento de uma linha.

Mais geralmente, se se considerar uma função de ponto, i.e., que a cada ponto do espaço associa um número, real ou complexo, essa função (notada aqui por \(ψ\) e \(ψ’\) respetivamente pelo observador \(O\) e \(O’\)) é um escalar se e só se:

\(\psi(x_1, x_2, x_3)= \psi'(x'_1, x'_2, x'_3)\)            (11)

Deve notar-se que as formas analíticas, i.e., as expressões destas funções são, em geral, diferentes porque têm exatamente que reproduzir o mesmo valor no mesmo ponto do espaço, sendo que tal ponto apresenta coordenadas diferentes para um e outro observadores. Por exemplo, considere-se a rotação de eixos atrás definida: a distância à origem \(O\) de um ponto de coordenadas (\(x_1, 0, 0\)) é, evidentemente, |\(x_1\)|. Para o outro observador \(O’\) cujos eixos rodaram de \(ϕ\) em torno do eixo comum \(x_3\equiv x'_3\), essa mesma distância é expressa por \(\), uma função analiticamente diferente da anterior mas que garante o mesmo valor numérico quando nelas se substituem as respetivas coordenadas do mesmo ponto do espaço.

Vetores

A eq. (10) fornece a relação entre as coordenadas do mesmo ponto \(P\) para os dois observadores considerados. Imaginemos, agora, um outro ponto \(Q\) cujas coordenadas são (\(y_1, y_2, y_3\)) para \(O\), e (\(y'_1, y'_2, y'_3\)) para \(O’\). A relação entre estas grandezas é dada pela mesma eq. (10):

\(y_i=X_i+M_{ji}y'_j\)

Então o segmento orientado \(\overrightarrow{PQ}\) é descrito pela diferença das coordenadas dos dois pontos, encontrando-se:

\(y_i-x_i=M_{ji}(y'_j-x'_j)\)            (12)

Esta diferença de coordenadas é, pois, independente das origens dos referenciais.

Designa-se por vetor polar, ou simplesmente vetor (FIGURA 3), uma grandeza definida por regras precisas e comuns aos dois observadores, a qual se exprime através de três números (\(A_1, A_2, A_3\)) para \(O\) e por outros três números (\(A'_1, A'_2, A'_3\)) para \(O’\), de tal forma que a relação entre estes conjuntos de números é exatamente a eq. (12):

\(A_i=M_{ji}A'_j\)            (13)

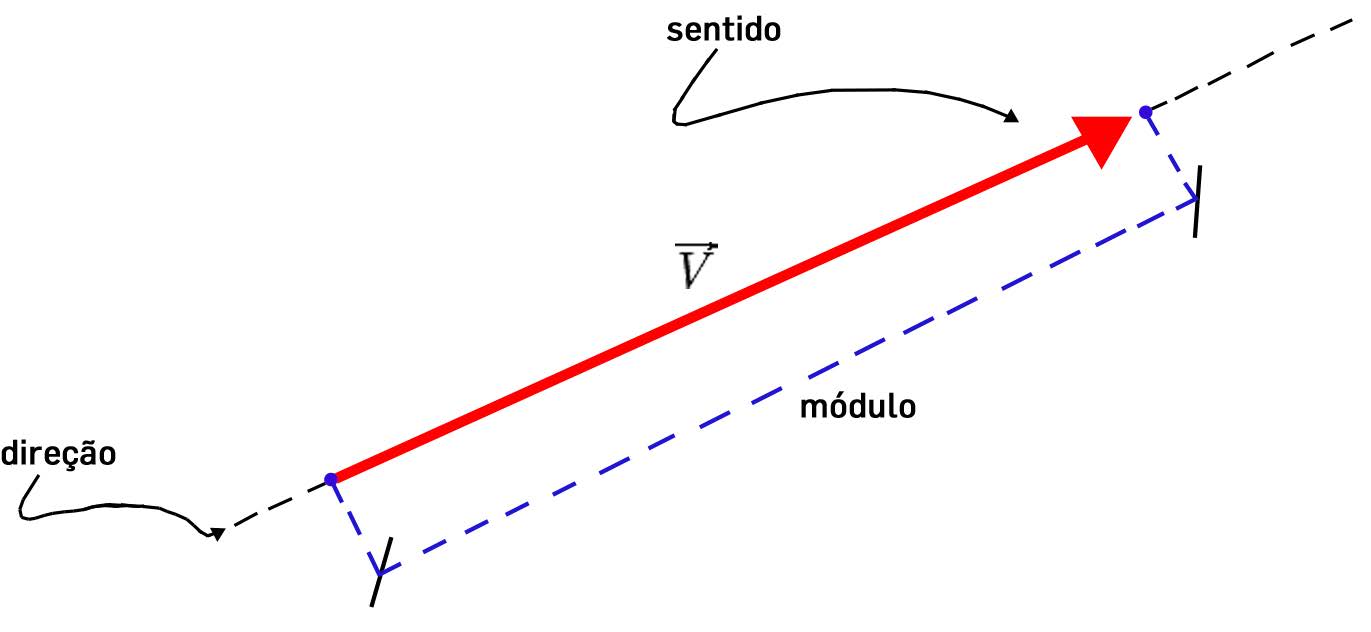
Segue-se, pois, que o segmento orientado \(\overrightarrow{PQ}\) é um vetor, sendo usada a mesma notação (uma seta sobre a letra) para \(\overrightarrow{A}\), um vetor de componentes (\(A_1, A_2, A_3\)) para \(O\) e (\(A'_1, A'_2, A'_3\)) para \(O’\). Com a eq. (8), a relação (13) pode ser invertida:

\(A'_i=M_{ik}A_k\)            (14)

Uma tal grandeza é independente dos observadores, embora, para cada um deles, ela se exprima através de componentes, em geral diferentes para os diferentes referenciais, mas relacionadas pelas eqs. (13) ou (14). São estas leis de transformação que definem um vetor e asseguram a sua independência dos observadores:

\(\overrightarrow{A}=A_i\overrightarrow{e}_i=M_{ji}A'_j\overrightarrow{e}_i=A'_j\overrightarrow{e}_j\)

A última igualdade resulta da eq. (6).

A velocidade de um ponto material é, talvez, o exemplo mais conhecido de vetor. Se tal ponto material é o ponto \(P\) atrás considerado, as suas coordenadas passam a depender do tempo (um escalar!), obrigando-nos a precisar a eq. (13):

\(x_i(t)=X_i+M_{ji}x'_j(t)\)

Deve, aqui, observar-se que se admitiu que nem \(O’\) se move em relação a \(O\) (as coordenadas \(X_i\) são fixas), nem o referencial de \(O’\) rodou em relação ao referencial de \(O\) (a matriz \([M]\), dos cossenos diretores, é também independente do tempo). O observador \(O\) define a velocidade do ponto material pelo conjunto (\(\frac{dx_1}{dt},\frac{dx_2}{dt},\frac{dx_3}{dt}\)) e o observador \(O’\) define a velocidade do mesmo ponto por (\(\frac{dx'_1}{dt},\frac{dx'_2}{dt},\frac{dx'_3}{dt}\)). Ora, derivando, em ordem ao tempo, a equação anterior, obtemos:

\(\frac{dx_i}{dt}=M_{ji}\frac{dx'_j}{dt}\)

Comparando com a eq. (13), estas derivadas definem um vetor, a velocidade \(\overrightarrow{v}\) do ponto material cujas componentes são (\(\frac{dx_1}{dt},\frac{dx_2}{dt},\frac{dx_3}{dt}\)), para o observador \(O\), e (\(\frac{dx'_1}{dt},\frac{dx'_2}{dt},\frac{dx'_3}{dt}\)) para o observador \(O’\). Derivando, novamente, a equação anterior, definimos um novo vetor, a aceleração \(\overrightarrow{a}\) do ponto material.

Há muitos outros exemplos de vetores em Física: a intensidade do campo gravítico \(\overrightarrow{G}\), a intensidade do campo elétrico \(\overrightarrow{E}\), a densidade de corrente elétrica \(\overrightarrow{l}\), etc.. Em todos eles, existe uma definição precisa que origina três números para um observador e outros três números para outro observador, sendo que estes conjunto de números estão relacionados pela eq. (13).

Usando a eq. (13) podemos definir duas outras importantes grandezas. Consideremos um outro vetor \(\overrightarrow{B}\), com componentes \(B_i\), para o observador \(O\), e \(B'_i\), para o observador \(O’\). Então:

\(B_i=M_{ji}=B'_j\)

Efetuemos o produto contraído \(A_iB_i\) e vejamos como ele se transforma:

\(A_iB_i=(M_{ji}A'_j)(M_{ki}B'_k)=M_{ji}M_{ki}A'_jB'_k=A'_jB'_j\)            (15)

Aqui, a última igualdade resultou da eq.(8). Quer dizer, o produto contraído de dois vetores é um escalar e,na verdade, reconhece-se o produto escalar dos vetores na eq. (15). O caso particular \(\overrightarrow{A}=\overrightarrow{B}\) define um escalar importante: o quadrado da grandeza do vetor \(\overrightarrow{A}\), soma dos quadrados das suas componentes. exemplos de produtos escalares abundam em Física: o trabalho realizado por uma força ou a sua potência, o calor libertado por efeito Joule, etc..

Outro caso importante resulta de se considerar uma função escalar tal como foi definida na eq. (11). Diferenciando ambos os membros daquela equação, obtemos a seguinte igualdade escalar:

\(\frac{\partial \psi}{\partial x_i}dx_i=\frac{\partial \psi'}{\partial x'_j}dx'_j\)

Ora, reconhecemos, em cada um dos membros, as componentes do vetor deslocamento infinitesimal \(d\overrightarrow{r}\), aparecendo, então, quer o 1º membro quer o 2º membro como um produto escalar, o que nos faz suspeitar que \(\frac{\partial \psi}{\partial x_i}\) e \(\frac{\partial \psi'}{\partial x'_j}\) são componentes do mesmo vetor para um e outro observadores. Podemos confirmar que assim é recorrendo à lei de transformação do vetor . Usando a eq. (14), tem-se:

\(\frac{\partial \psi}{\partial x_i}dx_i=\frac{\partial \psi'}{\partial x'_j}M_{ji}dx_i\)

Como as componentes do vetor deslocamento são arbitrárias e independentes, resulta:

\(\frac{\partial \psi}{\partial x_i}dx_i=\frac{\partial \psi'}{\partial x'_j}M_{ji}\)

que é a lei de transformação de um vetor (cf. eq. 13). Reconhecemos, aqui, o gradiente da função escalar:

\(\nabla\psi=\frac{\partial \psi}{\partial x_i}\overrightarrow{e}_i=\frac{\partial \psi'}{\partial x'_j}\overrightarrow{e}'_j=\nabla'\psi'\)            (16)

Note-se bem o significado deste resultado: um e outro observador definem os gradientes das suas funções, analiticamente diferentes, para concluírem que os vetores assim obtidos são iguais.

Recorda-se, rapidamente, que o vetor \(\nabla\psi\) é normal, em cada ponto, às superfície \(ψ = c = const\) e que o seu sentido indica o sentido do crescimento da função, fornecendo, inclusivamente, a distância de um ponto destas superfícies a outra, muito próxima (onde a constante toma o valor \(c+dc\)), através de \(dc_{\diagup\lceil\nabla\psi\rceil}\). Estes resultados obtêm-se diretamente das equações acima.

Tensores

Regressando aos vetores (arbitrários) \(\overrightarrow{A}\) e \(\overrightarrow{B}\) atrás considerados, iremos agora estudar como se transforma o produto \(A_iB_j\), notando que aqui se definem nove termos independentes.

O segundo observador também define as nove quantidades \(A'_iB'_j\). Ora, usando a eq. (14), obtemos:

\(A_iB_j=(M_{ki}A'_k)(M_{nj}B'_n)=M_{ki}M_{nj}A'_kB'_n\)            (17)

Definimos, agora, um tensor (cartesiano) de 2ª ordem como um conjunto de nove números, definidos por regras precisas, quer para o primeiro observador (designemo-los por \(T_{ij}\)) quer para o segundo (\(T'_{ij}\)), os quais estão relacionados como na eq. (17), i.e.,

\(T_{ij}=M_{ki}M_{nj}T'_{kn}\)            (18)

É esta, então, a lei de transformação de um tensor de 2ª ordem. Há muitos exemplos em Física de tais tensores: o tensor de inércia, na mecânica do sólido rígido; os tensores das tensões (FIGURA 4) e das deformações, na mecânica do sólido deformável; os tensores permitividade elétrica e permeabilidade magnética, bem como o tensor de Maxwell, no eletromagnetismo; etc.. Cada uma destas grandezas tem uma definição precisa para um e outro observador, mas para todos eles a lei de transformação é a eq. (18).

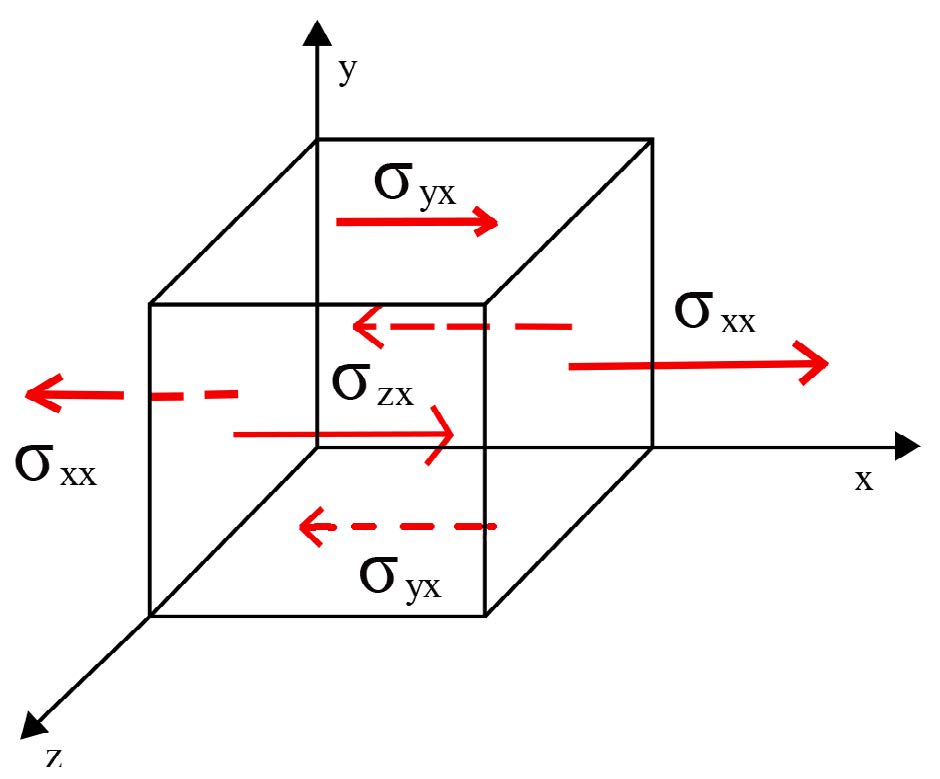
Por esta mesma razão, a matriz \([M]\), embora com dois índices, não é um tensor porque ela respeita à relação entre eixos de dois observadores.

Várias propriedades importantes e gerais deduzem-se facilmente a partir da eq. (18).

1ª Contraíndo os índices i e j (i.e., igualando-os e somando sobre os seus três valores possíveis), vem:

\(T_{ii}=M_{ki}M_{ni}T'_{kn}=\delta_{kn}T'_{kn}=T'_{kk}\)

A contração dos índices, designada por \(traço do tensor\), define um escalar.

2ª Multipliquemos ambos os membros da eq. (14) por um vetor \(w_j\), efetuando a contração deste índice:

\(T_{ij}w_j=M_{ki}M_{nj}T'_{kn}w_j\)

No 2º membro, reconhecemos a soma \(M_{nj}w_j=w'_n\), pela eq. (14). Assim:

\(T_{ij}w_j=M_{ki}T'_{kn}w'_n\)

Comparando com a eq. (13), vemos que \(T_{ij}w_j\) define um vetor: a contração de um tensor de 2ª ordem por um vetor dá um vetor. Pode-se provar o resultado inverso: suponhamos que temos definidas 9 quantidades \(T_{ij}\)para o observador \(O\) e outras nove quantidades \(T'_{kn}\) para o observador \(O’\). Se a equação anterior for verificada qualquer que seja o vetor \(\overrightarrow{w}\), podemos concluír que aquelas quantidades definem um tensor de 2ª ordem. É importante, na demonstração, a arbitrariedade do vetor. Um exemplo, aparentemente inesperado, é fornecido pelo símbolo de Kronecker, atrás definido. Admitamos, então, que \(T_{ij}=\delta_{ij}\) e, também, \(T'_{kn}=\delta_{kn}\).

Inserido na equação anterior, obtem-se:

\(w_i=M_{ki}w'_k\)

Mas esta é a lei de transformação do vetor arbitrário \(\overrightarrow{w}\). Então, concluímos que o símbolo de Kronecker é um tensor de 2ª ordem. Vejamos como se transforma: usando a genérica eq. (18), onde se identifica \(T'_{kn}=\delta_{kn}\) no 2º membro, obtemos:

\(M_{ki}M_{nj}\delta_{kn}=M_{ki}M_{kj}=\delta_{ij}\)

onde se recordou a eq. (8). Quer dizer, o símbolo de Kronecker, como tensor de 2ª ordem, tem a mesma forma para todos os observadores - diremos que é um tensor isotrópico.

3ª Um tensor de 2ª ordem é simétrico ou antissimétrico se satisfizer, respetivamente, \(S_{ij}=S_{ji}\) ou \(A_{ij}-A_{ji}\). É fácil ver que, no primeiro caso, o tensor tem seis elementos independentes e, no 2º caso, apenas três. Como se transformam estes tensores?

Começando pelo simétrico, tem-se:

\(M_{ki}M_{nj}S'_{kn}=M_{ki}M_{nj}S'_{nk}=M_{ni}M_{kj}S'_{kn}\)

Aqui, a 2ª igualdade é obtida trocando os índices mudos \(k\) e \(n\). O resultado final mostra que a simetria de um tensor é mantida na transformação. Consideremos, agora, a transformação de um tensor antissimétrico:

\(M_{ki}M_{nj}A'_{kn}=-M_{ki}M_{nj}A'_{nk}=-M_{ni}M_{kj}A'_{kn}\)

Aqui, procedemos, como antes, na troca dos índices mudos. A conclusão é a mesma: a antisimetria de um tensor é mantida pela sua lei de transformação.

Quer isto dizer que as simetria ou anti-simetria de um tensor (de 2ª ordem) são propriedades invariantes do tensor, verificadas por qualquer observador. Um exemplo evidente é o símbolo de Kronecker, um tensor simétrico.

4ª Vale a pena considerar com mais pormenor o caso de um tensor antissimétrico. Designemos as suas três entradas independentes da seguinte maneira:

\(𝛺_1\equiv-A_{23}=A_{32}\)

            \(Ω_2\equiv-A_{31}=A_{13}\)            (19)

\(Ω_3\equiv-A_{12}=A_{21}\)

Ora, sendo \(A_{ij}\) um tensor e sendo \(\overrightarrow{w}\) um vetor polar qualquer, então, como vimos, \(C_i=A_{ij}w_j\) é um vetor polar. Explicitando as suas componentes, encontramos:

\(C_1=A_{12}w_2+A_{13}w_3=-\Omega_3w_2+\Omega_2w_3\)

\(C_2=A_{21}w_1+A_{23}w_3=\Omega_3w_1-\Omega_1w_3\)

\(C_3=A_{31}w_1+A_{32}w_2=-\Omega_2w_1+\Omega_1w_2\)

Reconhecemos os segundos membros como as componentes de um produto vetorial o qual se escreve na sua forma habitual:

\(\overrightarrow{C}=\overrightarrow{Ω}\ \times \ \overrightarrow{w}\)            (20)

como se (\(\Omega_1,\Omega_2,\Omega_3\)) fossem as componentes de um vetor \(\overrightarrow{Ω}\). Contudo, \(\overrightarrow{Ω}\) não é um verdadeiro vetor (polar) porque aquelas componentes são, realmente, componentes de um tensor antissimétrico. Designa-se \(\overrightarrow{Ω}\) por vetor dual do tensor antissimétrico ou, mais habitualmente, por pseudo-vector ou vetor axial. Podemos verificar que \(\overrightarrow{Ω}\) se transforma, realmente, de maneira oposta à de um vetor polar considerando o exemplo simples da reflexão no plano \(x_2x_3\) atrás considerada (FIGURA 5).

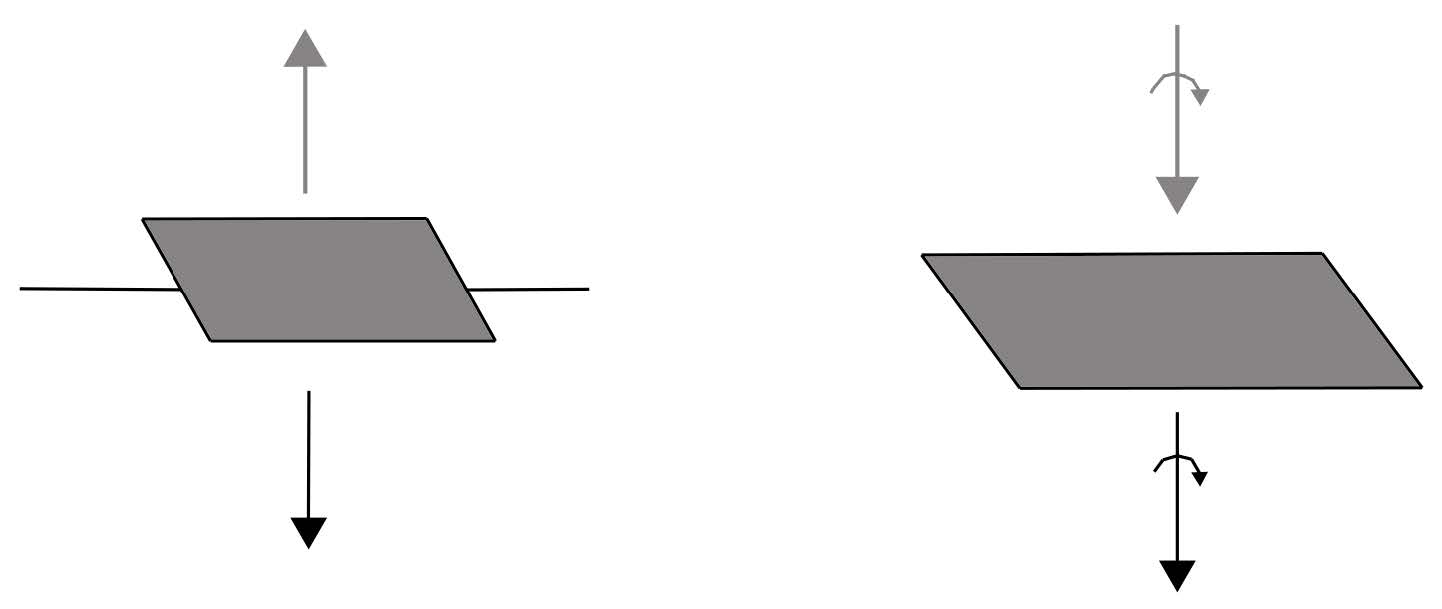
Usando a eq. (18) para a transformação do tensor \(A_{ij}\), com a matriz \([M]\) escrita naquele exemplo, obtemos:

\(\Omega_1\equiv-A_{23}=-M_{k2}M_{n3}A'_{kn}=-A'_{23}=\Omega'_1\)

\(\Omega_2\equiv-A_{31}=-M_{k3}M_{n1}A'_{kn}=-A'_{31}=-\Omega'_2\)

\(\Omega_3\equiv-A_{12}=-M_{k1}M_{n2}A'_{kn}=A'_{12}=-\Omega'_3\)

Compare-se com a transformação de um vetor polar, \(\overrightarrow{w}\), por exemplo, que se obtem da eq. (13):

\(w_1=M_{j1}w'_j=-w'_1\)

\(w_2=M_{j2}w'_j=w'_2\)

\(w_3=M_{j3}w'_j=w'_3\)

Um exemplo simples: imaginemos um pião a girar, no sentido direto, com o seu eixo dirigido segundo \(x_1\). O seu vetor rotação instantânea estará dirigido segundo este mesmo eixo. Veja-se a imagem no “espelho” \(x_2x_3\) - é um pião a girar no mesmo sentido, pelo que é idêntico o seu vetor rotação instantânea. Mas se dermos um passo em direção ao espelho, a nossa imagem dará um passo em sentido contrário - o deslocamento definido pelo passo é um verdadeiro vetor.

No entanto, é verdade que, para transformações entre referenciais com a mesma orientação, um vetor axial se comporta como um vector polar. É fácil verificar esta afirmação, repetindo os cálculos anteriores mas usando a matriz \([M]\) definida para o outro exemplo considerado atrás (rotação de eixos).

Voltando à eq. (20), recordamos que ela apenas reescreveu uma relação tensorial envolvendo o vetor \(\overrightarrow{w}\) e o tensor antissimétrico \(A_{ij}\), conduzindo a contração obtida, necessariamente, a um verdadeiro vetor \(\overrightarrow{C}\) (ver eq. 20). Assim, nesta equação, somos obrigados a concluir que o produto vetorial de um pseudo-vetor por um vetor polar conduz a um vetor polar. Alternativamente, o produto vetorial de dois vetores polares ou de dois pseudo-vetores resulta necessàriamente num vetor axial.

São muitos os exemplos em Física onde intervêm pseudo-vetores. São assim o momento cinético de uma partícula ou o (pseudo) vetor rotação instântanea de um sólido rígido, o campo magnético ou o momento magnético em eletromagnetismo, etc.. É de salientar que tais pseudo-vectores surgem em definições apropriadas mas acabam por aparecer em novos produtos vetoriais gerando, assim, verdadeiros vetores (por exemplo, o campo magnético dado pela lei de Biot-Savart faz-se sentir pela força de Lorentz - ambas as expressões contêm produtos vetoriais).

4ª Será, agora, óbvio que o produto escalar de um vetor por um pseudo-vector, por exemplo, \(\overrightarrow{Ω} \cdot \overrightarrow{w}\) tal como referidos acima. não é um verdadeiro escalar, dada a diferente lei de transformação dos termos nele presentes: é realmente um pseudo-escalar e como tal designado. Contudo, o produto escalar de dois pseudo-vectores é um verdadeiro escalar, de que são exemplos a potência de um sólido em rotação (produto escalar do seu momento cinético pelo pseudovector rotação instantânea) ou a energia de um magneto submetido a um campo magnético (produto escalar do seu momento magnético pela intensidade do campo magnético).