A partir do terceiro, cada número é pois igual à soma dos dois imediatamente anteriores.

É interessante notar que a sucessão \(\displaystyle\frac{F(n)}{F(n-1)}\) converge para um limite Φ que é o chamado número de ouro.

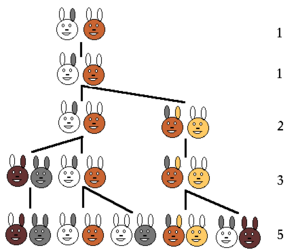
Foram criados pelo matemático italiano Fibonacci como um modelo simplificado do crescimento de uma população de coelhos.

Neste modelo:

\(F (n) =\) número total de pares de coelhos no ano \(n\)

O processo inicia-se no ano \(n = 0\) com um único par de coelhos jovens. Ao fim de cada ano, cada par dá origem a um novo par de descendentes. No entanto, cada par necessita de um ano para procriar o seu par de descendentes.

Fórmula de Binet

É possível mostrar a seguinte fórmula, chamada fórmula de Binet

\(F(n)=\displaystyle\frac{1}{\sqrt{5}}\left(\left(\displaystyle\frac{1+\sqrt{5}}{2}\right)^n- \left(\displaystyle\frac{1-\sqrt{5}}{2}\right)^n\right)\)

Algoritmos em Python

Apresentamos em seguida dois procedimentos em Python para a obtenção de qualquer número da sequência de números de Fibonacci, um deles um algoritmo recursivo e o outro um algoritmo iterativo.

Depois de uma das funções anteriores estar definida, quer seja a recursiva ou a iterativa, para obtermos, por exemplo, \(F(8)\) basta usarmos a instrução fibonacci(8).

No caso de querermos obter uma lista dos números de Fibonacci, e não só números isolados, podemos utilizar o procedimento abaixo descrito (em que o argumento da função range representa o número de números da sequência que queremos obter). No exemplo abaixo obtemos os dez primeiros números de Fibonacci.