Uma cifra consiste num procedimento que transforma um texto num outro, o criptograma, que se pretende ilegível para quem não possua um pedaço de informação (mantido secreto) a que se chama a chave. Essa transformação pode, por exemplo, substituir cada letra da mensagem original por outra letra, eventualmente de um outro alfabeto. Estas cifras de substituição são formadas por funções que fazem corresponder a cada caracter de um alfabeto um (outro) determinado caracter do mesmo (ou de outro) conjunto de símbolos. Assim podemos representar uma chave desta cifra como, por exemplo:

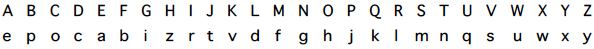
onde a primeira linha corresponde às letras da mensagem original e a segunda linha às que substituem cada uma dessas letras. Como o objetivo, para além de esconder o texto original, cifrando-o, é também que os destinatários, conhecendo a chave, o possam decifrar, estas transformações têm que ser reversíveis, ou seja, injetivas. No caso de se usar o mesmo alfabeto para as mensagens e para os respetivos criptogramas, estas cifras são, portanto, bijetivas, ou seja, permutações desse alfabeto.

Um ataque de “força bruta” a uma cifra de substituição envolve cerca de

26! = 403 291 461 126 605 635 584 000 ≈ 4 x 1026

tentativas, o que poderá dar a ideia de que esta cifra é seguríssima. É aqui que entra em campo a Criptanálise. Como observou o matemático árabe do séc. IX, al-Kindi, o facto de cada letra ser, ao longo de todo o texto, substituída sempre pelo mesmo símbolo, faz com que a frequência relativa de uma letra do texto original seja exatamente igual à frequência relativa da letra correspondente no criptograma. Esta observação permite um ataque devastador a este tipo de cifras. Basta construirmos a tabela de frequências relativas dos carateres da língua do criptograma e orientamos a pesquisa da chave fazendo corresponder as frequências encontradas no criptograma com as frequências médias de cada caracter na língua original. Ainda que possam ocorrer algumas variações significativas entre a frequência dos carateres no criptograma e a respetiva frequência média, em especial se o criptograma for pouco extenso, este método permite reduzir drasticamente o espaço de procura de chaves, tornando o ataque a este tipo de cifra relativamente fácil.

Para dificultar ataques baseados no estudo das frequências, foram criados sistemas que não cifram sempre da mesma forma cada uma das letras do texto original. Um exemplo é a chamada cifra de Vigenère, que usa ciclicamente as cifras de uma sequência de cifras de substituição. Esta nova cifra, que foi entusiasticamente denominada le chiffre indéchiffrable, veio, apesar disso, a ser quebrada no séc. XIX por C. Babbage (1791-1871). A ideia é que o período da cifra, o tamanho da sequência de cifras de substituição usadas, pode ser facilmente determinado através de uma pesquisa de padrões que se repetem a distâncias que correspondem a múltiplos desse período, e é depois possível proceder a um ataque estatístico como acima descrito. Claro que estes ataques só são eficazes se os textos intersetados forem suficientemente longos.

Durante o séc. XX foram inventados vários dispositivos eletromecânicos implementando cifras mais sofisticadas. Talvez o mais famoso desses dispositivos seja a máquina Enigma, versões da qual foram usadas pelas tropas alemãs durante a segunda guerra mundial.

Na cifra Enigma, a chave consiste no estado inicial da máquina, ou seja, a colocação e posicionamento de várias das suas componentes. Para decifrar uma mensagem cifrada numa máquina Enigma é necessário saber exatamente qual a configuração inicial da máquina que cifrou a mensagem. Usando ideias de várias áreas da matemática, nomeadamente Teoria de Grupos, que estuda, em particular, propriedades das permutações, alguns matemáticos “quintessencialmente puros”[1, p. 299], habituados a “pensar em espaços abstratos multidimensionais”[7, p. 199], conseguiu conceber métodos que foram múltiplas vezes bem sucedidos para encontrar as chaves usadas em certos dias por várias unidades militares alemãs.

Num mundo de comunicações digitais como o de hoje, onde são omnipresentes as transmissões de informação por ondas eletromagnéticas, não temos muitas vezes consciência do quanto dependemos de processos criptográficos. Quando se fala de Criptografia são as imagens de espiões, de mensagens diplomáticas e grandes segredos militares que imediatamente nos ocorrem. Este foi realmente o seu papel durante alguns milhares de anos, mas na segunda metade do séc. XX, quando passou a ser um campo de estudo da Matemática, e as transmissões digitais se popularizaram, a Criptografia quebrou as fronteiras do seu nicho de aplicação e invadiu as nossas vidas. Das emissões de televisão e telemóveis, às máquinas multibanco, na multitude das utilizações da internet, a Criptografia está lá, não só para garantir a segurança de segredos quando é caso disso, mas também para identificar e garantir identidades de interlocutores, pagamentos e integridade da transmissão de mensagens, efetuando tarefas das mais simples às mais complexas. Podemos dizer que grande parte das soluções encontradas para transpor interações que damos como garantidas no “mundo físico” para o “mundo virtual”, onde os interlocutores não se encontram fisicamente no mesmo local, foram e são dadas pela Criptografia, que usa hoje cada vez mais ferramentas matemáticas no próprio desenho das cifras.