Aqui, são apresentados dois exemplos típicos, mas bastante gerais: o trabalho realizado sobre um dieléctrico por um campo eléctrico externo e o trabalho realizado sobre um magnete por um campo magnético externo. Por externo entende-se que as fontes desses campos (a bateria que alimenta o condensador, o gerador que cria a corrente) não são parte do sistema de interesse. Em ambos os casos, começa-se por considerar constantes os campos aplicados, o que permite incorporar esses trabalhos na própria definição da energia interna dos sistemas considerados. Deste modo, essa redefinida energia interna só pode ser alterada quando os campos variam, obtendo-se, então, as conhecidas expressões do trabalho electromagnético sobre os sistemas de interesse. Este procedimento poderá parecer um pouco estranho e algo arbitrário, mas devemos lembrar-nos que, em Termodinâmica, um sistema é considerado isolado e, portanto, com uma energia interna constante, se não houver trocas de calor com outro sistema nem variação dos parâmetros externos que determinam a situação de equilíbrio, tais como pressão aplicada ou campos aplicados. A um nível mais fundamental, a energia interna não é mais que o Hamiltoniano do sistema, conceito fundamental da Mecânica e da Física Estatística, o qual se manterá constante se os campos externos permanecerem constantes.

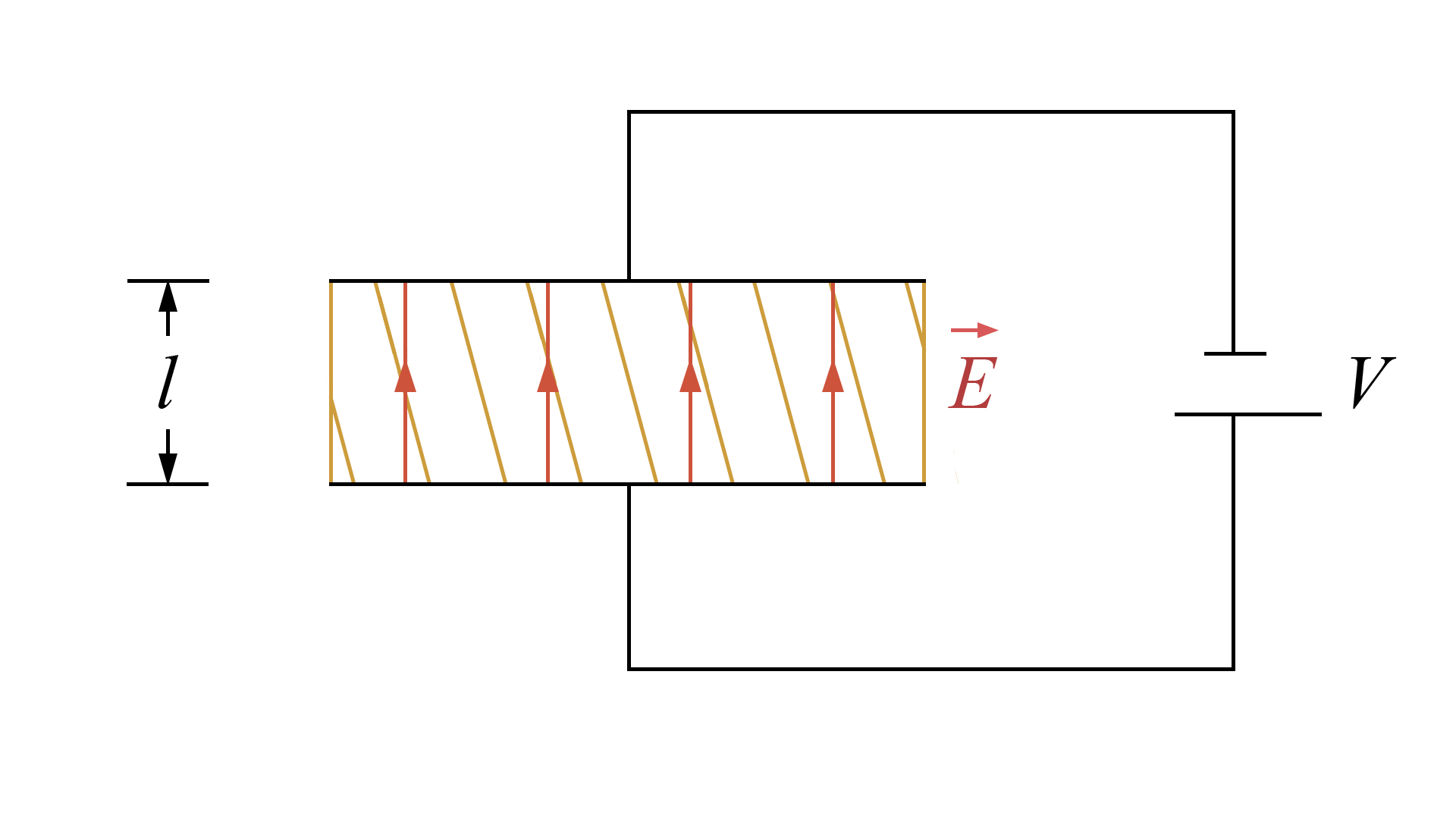
Consideremos a Figura 1: um condensador submetido a uma tensão constante \(V\), imposta pela bateria; no interior do condensador está introduzido um dieléctrico no qual existe uma polarização elétrica \(P\) paralela às linhas do campo aplicado \(E_{a}=\frac{V}{l}\). Suponhamos agora, que a polarização varia de \(\delta P\): então, há um aumento de carga positiva na face superior do dieléctrico igual a \(A\delta P\), onde \(A\) é a área da face, e um aumento de carga negativa \(-A\delta P\), na outra face. Como consequência, na placa superior do condensador, há um aumento de carga livre, negativa, \(-A\delta P\), e, na placa inferior, há um aumento de carga livre, positiva, \(A\delta P\). Quer dizer, a carga \(A\delta P\) foi transportada através da bateria da placa superior (ao potencial 0) para a placa inferior (ao potencial V), pelo que a bateria, sempre em tensão constante, realizou o trabalho, \(\delta W=AV\delta P=AlE_{a}\delta P\). Deste modo, a variação de energia interna do dieléctrico é \(dU=\delta W=AlE_{a}\delta P\) e como o campo aplicado permanece constante, podemos redifinir a energia interna de forma a incluir a interacção com o campo aplicado: \(U-AlE_{a}P\rightarrow U\). Assim, a variação desta redefinida energia interna resulta, apenas, da variação do campo aplicado: \(dU=-AlPdE_{a}\). Deverá notar-se que a energia interna contem, também, a interacção eléctrica entre os dipólos que definem a polarização; mas toda a interacção com o campo eléctrico aplicado ficou explicitada.

Apresentamos, a seguir, uma dedução mais geral e, por isso, mais formal. Num dieléctrico onde está definida uma polarização \(\overrightarrow{P}(\overrightarrow{r},t)\) que varia no tempo, existe uma corrente eléctrica \(\frac{\partial \overrightarrow{P}}{\partial t}\). Logo, o campo electrostático aplicado realiza a potência \(\int d\overrightarrow{r}\frac{\partial \overrightarrow{P}}{\partial t}\cdot \overrightarrow{E_{a}}(\overrightarrow{r})=\frac{d}{dt}\int d\overrightarrow{r}\overrightarrow{P}(\overrightarrow{r},t)\cdot \overrightarrow{E_{a}}(\overrightarrow{r})\), onde o integral é estendido ao domínio fixo ocupado pelo dieléctrico. Será, então, esta a variação da energia interna por unidade de tempo, i.e., \(\frac{dU}{dt}=\frac{d}{dt}\int d\overrightarrow{r}\overrightarrow{P}(\overrightarrow{r},t)\cdot \overrightarrow{E_{a}}(\overrightarrow{r})\). Assim, redefinindo a energia interna de modo a conter a interacção com o campo eléctrico aplicado \(U-\int d\overrightarrow{r}\overrightarrow{P}\cdot \overrightarrow{E_{a}}(\overrightarrow{r})\rightarrow U\), vemos que esta quantidade se conserva enquanto o campo aplicado permanecer constante. Deste modo, só há variação da energia interna redefinida se o campo aplicado variar, isto é, o trabalho realizado sobre tal sistema é:

\(\delta W=-\int d\overrightarrow{r}\overrightarrow{P}(\overrightarrow{r})\cdot \delta \overrightarrow{E_{a}}(\overrightarrow{r})\)

Note-se que a energia interna redefinida contem, para um único dipólo eléctrico \(\overrightarrow{p}\), o termo de interação \(-\overrightarrow{p}\cdot \overrightarrow{E_{a}}\).

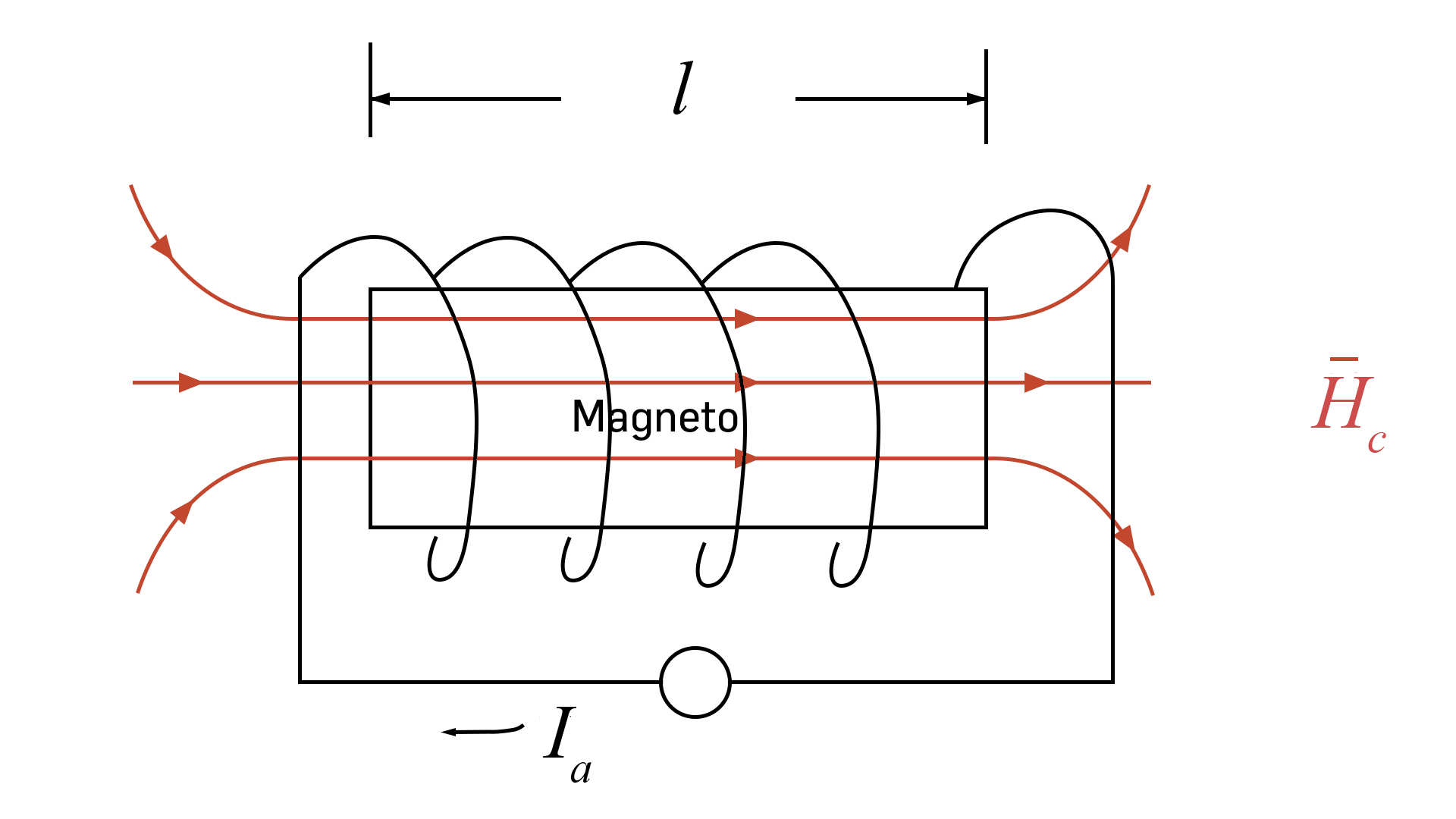
A FIGURA 2 representa um solenóide com \(N\) espiras, comprimento \(l\), enrolado em torno de um magnete cilíndrico, com secção recta da área \(A\). O circuito eléctrico é alimentado por um gerador de corrente que mantem sempre uma intensidade de corrente \(l\). O campo magnético aplicado no interior do solenóide é longitudinal, com amplitude \(H_{a}=\frac{N}{l}l\). É este, também, o campo magnético no interior do magnete, pelo que a excitação magnética dentro do magnete é \(B=\mu _{0}(H_{a}+M)\), onde \(\mu _{0}\) é a permeabilidade magnética do vazio, uma constante fundamental. Admitamos, agora, que a magnetização varia de \(\delta M\), mas mantendo-se a corrente sempre constante. Haverá, então, uma variação da excitação magnética \(\delta B=\mu _{0}\delta M\) e, portanto, uma variação do fluxo magnético através do solenóide, \(\delta \Phi =NA\delta B=\mu _{0}NA\delta M\), originando (lei de Faraday) uma força electromotriz induzida \(\varepsilon =-\frac{\partial \Phi }{\partial t}\). Não fosse o gerador de corrente e esta f.e.m. iria alterar a corrente; mas o gerador mantem sempre a mesma corrente, pelo que compensa automaticamente esta f.e.m., Isto é, o gerador cria a f.e.m. Não fosse o gerador de corrente e esta f.e.m. iria alterar a corrente; mas o gerador mantem sempre a mesma corrente, pelo que compensa automaticamente esta f.e.m., Isto é, o gerador cria a f.e.m. \(-\varepsilon =\frac{\partial \Phi }{\partial t}\) e, portanto, despende a potência \(I\frac{\partial \Phi }{\partial t}\). De forma equivalente, o gerador realiza o trabalho \(\delta W=I\delta \Phi =\mu _{0}NAI\delta M=\mu _{0}(Al)\frac{N}{l}I\delta M=\mu _{0}AlH_{a}\delta M\) durante o intervalo de tempo em que variou a magnetização. É, então, este, o trabalho realizado sobre o magnete, originando a variação da sua energia interna \(dU=\delta W=\mu _{0}AlH_{a}\delta M\). Como o campo aplicado permanece constante, podemos redefinir a energia interna de modo a incluir a interacção do magnete com o campo aplicado: \(U-\mu _{0}AlH_{a}M\rightarrow U\). Deste modo, a variação desta redefinida energia interna deve-se unicamente à variação do campo aplicado: \(dU=-\mu _{0}AlM\delta H_{a}\), sendo este, então, o trabalho realizado sobre o sistema que inclui a sua interacção com o campo aplicado. Deve notar-se que a energia interna contem, também, a interacção entre os dipólos magnéticos que constituem o magnete, mas toda a interacção com o campo aplicado ficou explicitada.

Apresentamos, a seguir, uma dedução mais geral e, por isso, mais formal. Em electromagnetismo, apenas o campo eléctrico realiza trabalho. Quando há uma variação de magnetização, é induzido um campo eléctrico \(\overrightarrow{E}\) que, por si só, iria fazer variar a corrente num circuito. Se queremos manter esta corrente constante, o gerador compensa, automaticamente, este campo induzido gerando um campo \(-\overrightarrow{E}\) e, portanto, realizando a potência, por unidade de volume, \(-\overrightarrow{E}\cdot \overrightarrow{i_{a}}\), onde \(\overrightarrow{i_{a}}\) é a densidade de corrente aplicada. Assim, a potência dispendida pelo gerador é \(-\int d\overrightarrow{r}\overrightarrow{E}\cdot \overrightarrow{i_{a}}\). Ora, pela lei de Maxwell-Ampére, o campo magnético aplicado e a corrente aplicada estão relacionados por \(\overrightarrow{i_{a}}=\bigtriangledown \wedge \overrightarrow{H_{a}}\). Substituindo e integrando por partes, obtem-se a expressão equivalente para a potência fornecida pelo gerador: \(-\int d\overrightarrow{r}\overrightarrow{H_{a}}\cdot \bigtriangledown \wedge \overrightarrow{E}=\int d\overrightarrow{r}\overrightarrow{H_{a}}\cdot \frac{\partial \overrightarrow{B}}{\partial t}\), onde a segunda expressão resulta da lei de Maxwell-Faraday. Como \(\overrightarrow{B}=\mu _{0}(\overrightarrow{H}+\overrightarrow{M})\), qual a diferença entre este campo magnético \(\overrightarrow{H}\) e o campo aplicado \(\overrightarrow{H_{a}}\)? Será evidente que \(\overrightarrow{H}=\overrightarrow{H_{a}}+\overrightarrow{H_{d}}\), onde \(\overrightarrow{H_{d}}\) é o campo devido ao próprio magnete. Mas tal campo satisfaz a \(\bigtriangledown \wedge \overrightarrow{H_{d}}=0\) porque é originado, apenas, nas correntes microscópicas dos dipólos magnéticos que constituem o magnete e que definem o momento magnético. Tendo rotacional nulo, o campo \(\overrightarrow{H_{d}}\) deriva de um gradiante: \(\overrightarrow{H_{d}}=\bigtriangledown \psi \), pelo que a sua contribuição para o integral anterior é nula: \(\int d\overrightarrow{r}\overrightarrow{H_{a}}\cdot \frac{\partial \overrightarrow{H_{d}}}{\partial t}=\int d\overrightarrow{r}\overrightarrow{H_{a}}\cdot \bigtriangledown \frac{\partial \psi }{\partial t}=-\int d\overrightarrow{r}\frac{\partial \psi }{\partial t}\bigtriangledown \cdot \overrightarrow{H_{a}}=0\) (para o campo aplicado é \(\overrightarrow{H_{a}}=\frac{\overrightarrow{B_{a}}}{\mu _{0}}\) e qualquer excitação magnética tem divergência nula). Então, a potência do gerador pode reescrever-se \(\mu _{0}\int d\overrightarrow{r}\overrightarrow{H_{a}}\cdot \frac{\partial M}{\partial t}=\frac{d}{dt}\int d\overrightarrow{r}\mu _{0}\overrightarrow{H_{a}}\cdot \overrightarrow{M}\), originando, portanto, a variação de energia interna \(\frac{dU}{dt}=\frac{d}{dt}\int d\overrightarrow{r}\mu _{0}\overrightarrow{H_{a}}\cdot \overrightarrow{M}\), levando à redefinição da energia interna \(U-\int d\overrightarrow{r}\mu _{0}\overrightarrow{H_{a}}\cdot \overrightarrow{M}\rightarrow U\). Assim, esta energia interna redefinida contem a interacção com o campo magnético aplicado e só pode variar se este variar, isto é, o trabalho realizado por este campo magnético é:

\(\delta W=-\int d\overrightarrow{r}\mu _{0}\overrightarrow{M}(\overrightarrow{r})\cdot \delta \overrightarrow{H_{a}}(\overrightarrow{r})\)

Note-se que a energia interna redefinida contem, para um único dipólo magnético \(\overrightarrow{\mu }\), o termo de interção \(-\overrightarrow{\mu }\cdot \overrightarrow{B_{a}}\).

O leitor poderá ter a seguinte dúvida: se, no caso do dieléctrico, o campo eléctrico aplicado é não depende do tempo, então por que pode variar a polarização? De modo análogo, no caso do magnete, se o campo magnético aplicado não depende do tempo por que pode variar a magnetização? Em ambos os casos, a resposta é a mesma: polarização ou magnetização podem variar porque é, por exemplo, alterada a temperatura ou pressão, mas também, espontaneamente, por reorientação de domínios microscópicos ou porque ocorre uma transição de fase. Estes são tópicos muito interessantes mas que estão para além dos objectivos deste trabalho.