Os modelos compartimentais são modelos matemáticos em que a variação temporal de uma determinada grandeza ou característica físico-química se faz através de conjuntos bem definidos, a que chamamos compartimentos^{1, 2}. A taxa de transferência entre compartimentos é sempre proporcional à quantidade desta grandeza ou característica em cada compartimento. Estes modelos têm ampla utilização em muitas áreas científicas com ênfase nas ciências biomédicas, estudos populacionais, epidemiologia e informática.

Construção de modelos compartimentais

Considere-se o modelo compartimental mais simples possível - um modelo a dois compartimentos, em que um compartimento (A) transfere uma determinada grandeza para outro (B):

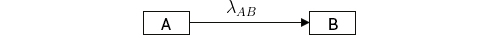
Os elementos do compartimento A vão sendo “transferidos” para os elementos do compartimento B com uma taxa de transferência \(\lambda _{AB}\), numa relação que pode ser escrita da seguinte forma:

\(\left\{\begin{matrix} \frac{dA}{dt}=-\lambda _{AB}A\\ \\ \frac{dB}{dt}=\lambda _{AB}A \end{matrix}\right.\) (1)

Ora, nós conhecemos estas equações. Não são mais do que as equações diferenciais cuja solução é a conhecida função exponencial, tanto com expoente positivo, como negativo:

\(\left\{\begin{matrix} f_{A}\left ( t \right )=f_{0A}e^{-\lambda t}\\ \\ f_{B}\left ( t \right )=f_{0A}\left ( 1-e^{-\lambda t} \right ) \end{matrix}\right.\) (2)

Esta função é seguramente conhecida de todos, e tem inúmeras aplicações, como por exemplo no caso do decaimento radioactivo. Considerando um radionuclídeo em decaimento com uma determinada atividade num instante \(t=0,A\left ( 0 \right )=A_{0}\), a solução da equação (1) para A é:

\(A\left ( t \right )=A_{0}e^{-\lambda t},\) (3)

Neste caso, \(\lambda _{AB}=\lambda =\frac{In\left ( 2 \right )}{T_{1/2}}\), e \(T_{1/2}\) é o tempo de semivida característico do radionuclídeo.

Em termos do modelo compartimental, este fenómeno pode ser compreendido da seguinte forma: o compartimento A representa o conjunto de elementos “pai”, e o compartimento B representa o conjunto de elementos “filho”. O compartimento A está a “transferir” o seu conteúdo, neste caso, por decaimento radioativo, para o compartimento B. A solução da equação que descreve esta transferência compartimental é dada pela equação (3).

No entanto, este modelo compartimental simples não nos traz nada de novo, dado que a lei do decaimento radioativo pode ser compreendida sem o auxílio à utilização de compartimentos.

Aplicações em ciências biomédicas

Vamos tentar imaginar então, algo mais complicado, como o seguinte modelo a três compartimentos:

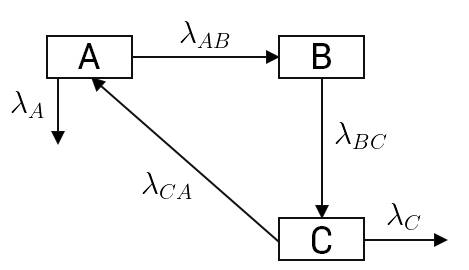
Que descreve as seguintes equações diferenciais:

\(\left\{\begin{matrix} \frac{dA}{dt}=\lambda _{CA}C-\left ( \lambda _{AB}+\lambda _{A} \right )A,\\ \\ \frac{dB}{dt}=\lambda _{AB}A-\lambda _{BC}B,\\ \\ \frac{dC}{dt}=\lambda _{BC}B-\left ( \lambda _{CA}+\lambda _{C}C \right ). \end{matrix}\right.\) (4)

Este modelo não tem uma solução analítica como no caso de (1). Na verdade, na maioria dos casos, os modelos compartimentais resolvem-se numericamente, utilizando, por exemplo, um método de Runge-Kutta de 4ª ordem, apesar de qualquer método numérico, desde que adequado, possa ser utilizado. Outras vezes, podem possuir soluções analíticas exatas, ou aproximadas.

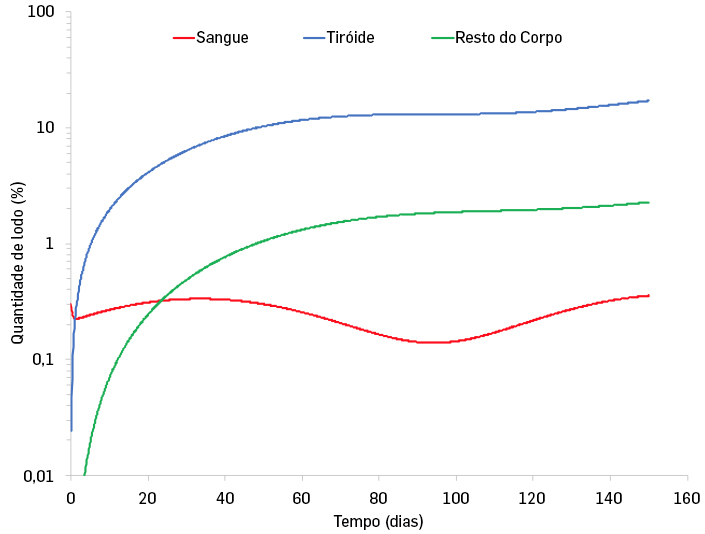
Na FIGURA 3, apresentamos uma solução para o sistema de equações (4) usando um método de Runge-Kutta.

Este modelo é utilizado para descrever a biocinética do iodo no nosso organismo³, em que o compartimento A representa o sangue, e transfere o seu conteúdo (neste caso iodo) para o compartimento B (que representa a tiroide) com uma taxa \(\lambda _{AB}\), e expele-o através do sistema urinário, com uma taxa \(\lambda _{A}\). Como vimos, o compartimento B representa a tiroide, que recebe do compartimento A como explicado acima, iodo, e transfere-o, com uma taxa \(\lambda _{BC}\), para o resto do corpo, representado pelo compartimento C. O compartimento C recebe iodo à taxa \(\lambda _{BC}\), e expele-o, através do sistema intestinal, com uma taxa \(\lambda _{C}\). Os valores dos parâmetros são determinados experimentalmente através de medições dos níveis de iodo em cada sistema de órgãos referido acima. Considerando uma concentração periódica de iodo no sangue que reflita um consumo diário de iodo, veja-se como rapidamente os valores de iodo na tiroide e resto do corpo convergem para valores constantes, de cerca de 24% na tiroide e 2% no resto do corpo, como pode ser visto na FIGURA 3.

A importância deste modelo deve-se ao facto de, como é sabido, o iodo ser fundamental para o correto metabolismo da tiroide. Para além disso, isótopos radioativos do iodo são usados, tanto em terapia como para imagem da tiroide em medicina.

Outro modelo compartimental com o mesmo número de compartimentos, mas distribuídos de forma diferente, e bastante utilizado em farmacocinética, para o estudo e desenvolvimento de novos fármacos, é chamado de “modelo a três compartimentos”⁴, e pode ser representado através do seguinte esquema:

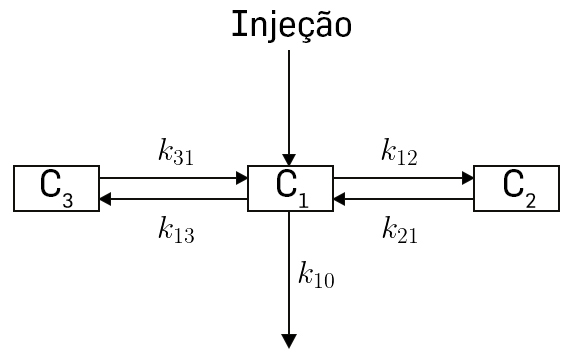
Na forma mais simplificada do modelo, assume-se que a administração do fármaco se faz por injeção, e portanto a incorporação no primeiro compartimento é imediata (ou seja, a totalidade do fármaco, no instante \(t=0\), no compartimento \(C1\). O compartimento \(C_{1}\) representa o plasma sanguíneo, e os dois compartimentos \(C_{2}\) e \(C_{3}\) são compartimentos ditos “periféricos”, um representando um metabolismo lento do fármaco (tecido gordo) e o outro, um rápido (tecido magro). As equações diferenciais são:

\(\left\{\begin{matrix} \frac{dC_{1}\left ( t \right )}{dt}=-\left ( k_{10}+k_{12}+k_{13} \right )C_{1}\left ( t \right )+k_{21}C_{2}\left ( t \right )+k_{31}C_{3}\left ( t \right ),\\ \\ \frac{dC_{2}\left ( t \right )}{dt}=k_{12}C_{1}\left ( t \right )-k_{21}C_{2}\left ( t \right )\\ \\ \frac{dC_{3}\left ( t \right )}{dt}=k_{13}C_{1}\left ( t \right )-k_{31}C_{3}\left ( t \right ) \end{matrix}\right.\) (5)

Apesar do sistema de equações descrito em (4) não ter uma solução analítica, é possível fazer uma aproximação ao valor da concentração do fármaco no plasma, \(C_{1}\left ( t \right )\):

\(C_{1}\left ( t \right )\cong Ae^{-\alpha t}+Be^{-\beta t}+Ce^{-\gamma t}\) (6)

O primeiro termo \(Ae^{-\alpha t}\) representa a fase de distribuição do fármaco no organismo, logo após incorporação no plasma; o segundo termo \(Be^{-\beta t}\) representa a fase de eliminação em que o fármaco se encontra a ser eliminado do próprio plasma e tecido magro; e finalmente o terceiro termo \(Ce^{-\gamma t}\) representa a fase terminal, em que o fármaco se encontra a ser eliminado muito lentamente pelo resquício acumulado no tecido gordo do corpo.

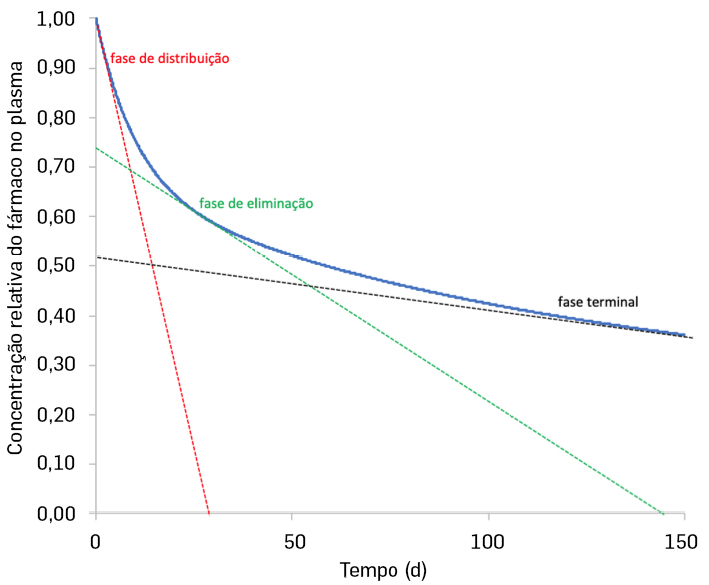
Na FIGURA 5 vemos um gráfico da evolução da concentração de um fármaco com valores escolhidos arbitrariamente apenas para ilustração. Este modelo permite compreender de forma relativamente simples como um fármaco é absorvido e expelido pelo corpo, o que é essencial para o estudo da sua aplicabilidade clínica.

APLICAÇÕES EM EPIDEMIOLOGIA

1 - Modelo SIR e SIRS

Os modelos compartimentais têm uma enorme aplicabilidade em ciências biológicas. Mas existe outra área em que estes modelos têm ampla aplicação, que é a epidemiologia e o estudo das populações⁵.

Para ilustração, e agora que estamos familiarizados com os modelos compartimentais, imaginemos o seguinte modelo para descrever a evolução de uma doença infecciosa numa determinada população:

A população é dividida em compartimentos de acordo com o estado de cada elemento relativamente à doença - Os suscetíveis (S) a contrair a doença, os infetados (I) pela doença, e os que foram mortos ou recuperados da doença (R). Este modelo também é um modelo a três compartimentos, mas tem uma particularidade diferente dos restantes modelos referidos acima. Neste modelo, a taxa de transferência do primeiro para o segundo compartimento é não só proporcional ao valor do primeiro, como também ao valor do segundo.

De facto, não só quanto maior a percentagem de suscetíveis mais rapidamente os suscetíveis contrairão a doença, como também quanto maior a percentagem de infetados mais rapidamente os suscetíveis contrairão a doença. Desta forma, as equações diferenciais para este modelo são:

\(\left\{\begin{matrix} \frac{dS\left ( t \right )}{dt}=-\frac{\beta }{N}S\left ( t \right )I\left ( t \right ),\\ \\ \frac{dI\left ( t \right )}{dt}=-\frac{\beta }{N}S\left ( t \right )-\gamma I\left ( t \right )\\ \\ \frac{dR\left ( t \right )}{dt}=\gamma I\left ( t \right ) \end{matrix}\right.\) (7)

E ainda uma quarta equação implícita que é \(S\left ( t \right )+I\left (t \right )+R\left ( t \right )=N\). Para além disso, este modelo possui ainda duas constantes de proporcionalidade, \(\beta \), que é o número de contactos que cada pessoa efetua por unidade de tempo (normalmente dias) no início do surto, c0, multiplicada pela probabilidade de contágio em cada contacto no início do surto, \(p_{0}\), e que é normalmente denominada taxa de transmissão:

\(\beta =p_{0}c_{0}\) (8)

E ainda \(\gamma \), que é a fração dos infetados que se recuperam ou morrem por unidade de tempo, normalmente denominada por taxa de recuperação ou remoção.

A partir deste modelo, podemos ainda definir a seguinte quantidade:

\(R_{0}=\beta _{/\gamma }=p_{0}c_{0}\tau \) (9)

que é o número médio de contactos de uma pessoa infetada por dia, multiplicada pela probabilidade de contágio num contacto, no início do surto multiplicada pelo tempo de infeção \(\tau =\gamma ^{-1}\) característico de cada doença infeciosa. Este número representa o valor expectável de infeções secundárias provocadas por uma infeção primária, e é normalmente chamado de número de reprodução de base. A sua importância prende-se com o facto de o seu valor ajudar a compreender de uma forma simples como será a evolução de uma determinada doença infeciosa: quando \(R_{0}\geq 1\) ocorrerá um surto epidémico; quando \(R_{0}< 1\) a doença não terá força suficiente para se espalhar, e acabará por desaparecer. A título de exemplo de algumas doenças conhecidas, a gripe tem um \(R_{0}\) de cerca de 1, o sarampo um valor entre 12 e 18^{6, 7}, e estima-se que a atual epidemia de COVID-19 tenha um valor de \(R_{0}\) que possa chegar a cerca de 7, apesar da maioria dos estudos apontar para um valor mais próximo de 2-3⁸

Na FIGURA 7 é mostrado um exemplo da evolução da trajetória de uma doença infecciosa com um \(R_{0}=4\) numa população de 10 milhões de habitantes.

Ao fim de um determinado tempo, no caso específico deste modelo, cerca de 100 dias, quase toda a população passou do estado suscetível para o estado removido, e neste período, uma vasta percentagem da população foi infetada, no caso do exemplo, cerca de 40%.

Para além do \(R_{0}\) podemos ainda definir o número de reprodução efetivo (\(R_{eff}\)), que representa o valor expectável de infeções secundárias provocadas por infetados a um instante t após o início do surto, ou seja \(R_{eff}\left ( t \right )=p_{t}c_{t}\tau \), em que \(p_{t}\) representa a probabilidade de contágio no instante \(t\), e \(\tau =\gamma ^{-1}\) continua a ser o tempo de infeção característico de cada doença. Pela expressão percebemos que \(R_{eff}\left ( 0 \right )=R_{0}\).

Quando o valor de \(R_{eff}\) passa a ser inferior a 1, e o surto passa a entrar em fase decrescente. No final do surto epidémico, é possível pensar que nem todos os suscetíveis adquiriram imunidade (ou esta não é duradoura). Desta forma, os removidos têm a possibilidade de serem reinfetados. É possível introduzir isto na equação acrescentando um termo \(\xi R\left ( t \right )\):

\(\left\{\begin{matrix} \frac{dS\left ( t \right )}{dt}=-\frac{\beta }{N}S\left ( t \right )I\left ( t \right )+\xi R\left ( t \right )\\ \\ \frac{dI\left ( t \right )}{dt}=-\frac{\beta }{N}S\left ( t \right )-\gamma I\left ( t \right )\\ \\ \frac{dR\left ( t \right )}{dt}=\gamma I\left ( t \right )-\xi R\left ( t \right ) \end{matrix}\right.\) (10)

Que representa uma taxa de transferência dos removidos para os suscetíveis de contraírem novamente a doença. Este tipo de modelos é conhecido como SIRS (Suscetíveis-Infetados- Removidos-suscetíveis) e permite modelar surtos epidémicos em que a imunização não está garantida.

Introduzindo este parâmetro no modelo da FIGURA 6 obtemos:

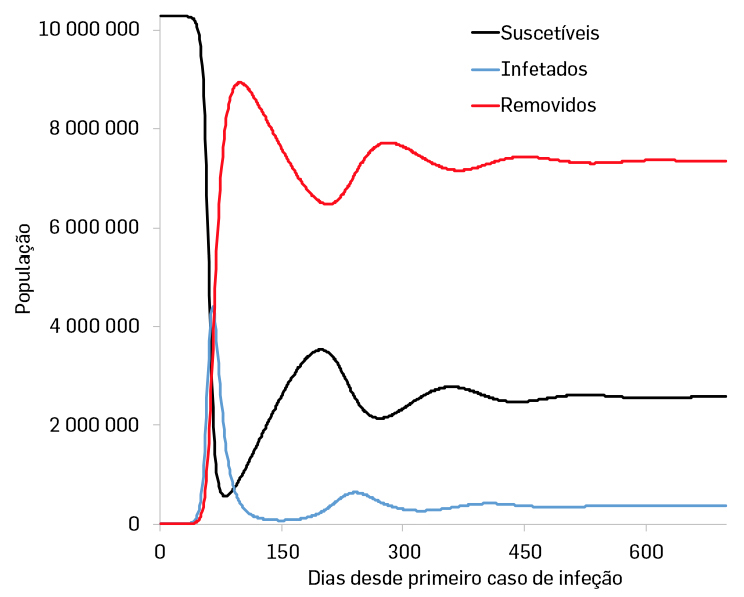
Pode-se observar que, para além de um primeiro surto com um pico pronunciado, teremos uma segunda e até uma terceira vaga que, no entanto, terão sempre uma força inferior à do primeiro surto.

2 - Modelo SEIR e SEIRS

É sabido que as doenças infeciosas possuem um tempo de incubação que pode durar de um até vários dias (como a gripe), ou mesmo semanas (como a tuberculose), ou ainda meses ou anos. Durante este período, o indivíduo encontra-se infetado, mas ainda não está contagioso. De forma a levar isto em consideração, existem os modelos do tipo SEIR (Suscetíveis- Expostos-Infetados-Removidos), ou ainda SEIRS(Suscetíveis-Expostos-Infetados- Removidos-Suscetíveis) quando queremos considerar que não é adquirida imunidade.

Nestes modelos é acrescentado um compartimento “Expostos” que considera o descrito acima. O valor de \(\sigma ^{-1}\) é o tempo de incubação da doença. As equações são, portanto:

\(\left\{\begin{matrix} \frac{dS\left ( t \right )}{dt}=-\frac{\beta }{N}S\left ( t \right )I\left ( t \right )+\xi R\left ( t \right )\\ \\ \frac{dE\left ( t \right )}{dt}=-\frac{\beta }{N}S\left ( t \right )I\left ( t \right )-\sigma E\left ( t \right )\\ \\ \frac{dI\left ( t \right )}{dt}=\sigma E\left ( t \right )-\gamma I\left ( t \right )\\ \\ \frac{dR\left ( t \right )}{dt}=\gamma I\left ( t \right )-\xi R\left ( t \right ) \end{matrix}\right.\) (11)

Como o tempo incubação do agente infecioso atrasa o início do período de contágio, o pico de infetados vai ocorrer um pouco mais tarde que num modelo SIR. No entanto, como mais nenhum parâmetro é alterado, o pico de infetados tem a mesma forma, e as considerações feitas para os modelos SEIR são as mesmas que as descritas para os modelos SIR acima.

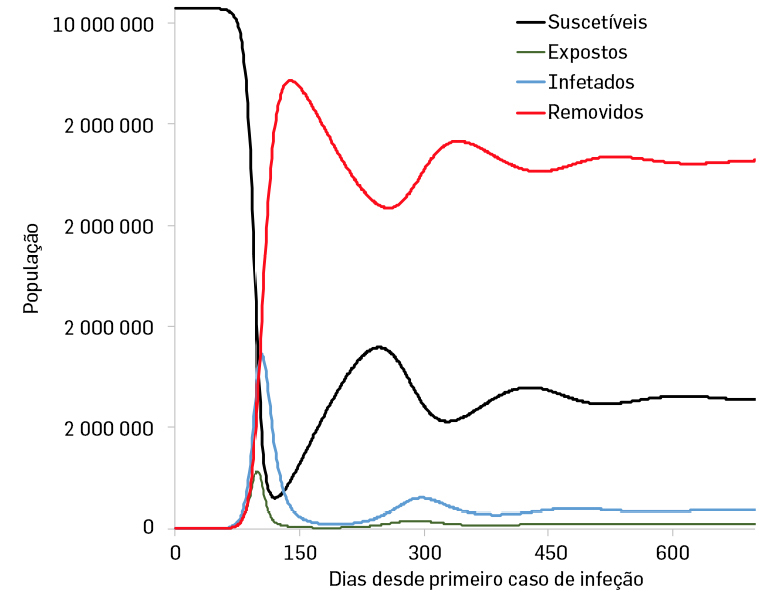
Este modelo é bastante mais realista que o SIR em especial para patógenos com períodos de incubação relativamente elevado. Uma solução gráfica para um modelo SEIRS, usando os mesmos parâmetros utilizados para modelo como descritos nas figuras dos gráficos apresentado na FIGURA 9.

3 – Outros modelos

Na verdade, os surtos epidémicos podem possuir características não previstas nos dois tipos de modelos anteriores. Por exemplo, é sabido que muitos surtos epidémicos incluem indivíduos assintomáticos que são também contagiosos, ou seja, capazes de transmitir a doença aos suscetíveis. Ainda, pode ser conveniente incluir no modelo compartimentos que sejam capazes de modelar a evolução de casos hospitalizados ou mesmo fazer a distinção entre mortos e recuperados nos removidos. Podemos ainda querer, por exemplo modelar a existência de um grupo de pessoas que foi posta em quarentena, tanto de forma preventiva, como após se tornarem contagiosos. Surgem assim vários outros tipos de modelos, dos quais deixamos aqui alguns exemplos⁹:

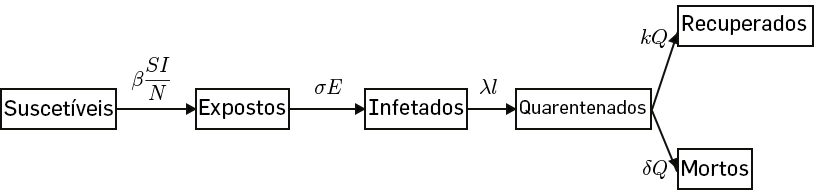
• Modelos do tipo SEIR-QD (Suscetíveis-Expostos-Infetados-Removidos-Quarentenados- Mortos (Deceised do inglês). Neste modelo são considerados dois compartimentos extra, em que os infetados são colocados em quarentena com uma determinada taxa temporal.

• Modelos do tipo SEIR-AH¹⁰ (Susceptíveis-Expostos-Infetados-Removidos-Assintomáticos- Hospitalizados). Neste modelo, considera-se a existência de um quadro assintomático, em que os indivíduos neste compartimento não apresentam nenhum sintoma, porém são contagiosos, i.e. capazes de transmitir a doença. Considera-se também a existência de um compartimento que represente os hospitalizados

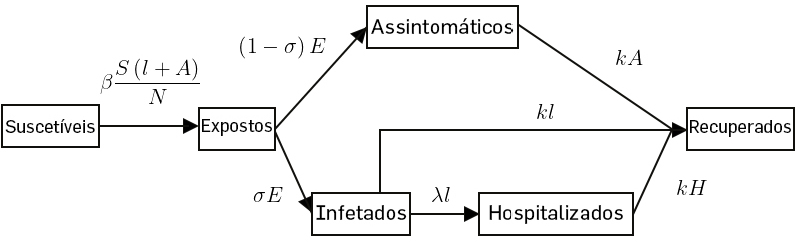
Entre muitas outras variações, dependendo do tipo de surto que estiver a ser estudado, assim como do grau de especificidade com que se quer conseguir a modelação. Muitas vezes a escolha do modelo vai depender do tipo de observáveis que podem ser obtidas. No caso dos SEIR-AH por exemplo, a existência de hospitalizados permite melhor inferir sobre os parâmetros do modelo, dado que, em conjunto com os dados sobre o número de mortos, são os dados mais fiáveis de um surto epidémico.

4 – Limitações dos modelos compartimentais em epidemiologia

Os modelos do tipo compartimental são determinísticos, o que significa que dadas as condições iniciais, o modelo irá sempre fornecer os mesmos resultados. Isto vai contra a natureza estocástica de uma epidemia, em que as probabilidades jogam um papel essencial. Para além disso, estes modelos analisam a evolução dos diferentes compartimentos como um todo, não permitindo inferir sobre epifenómenos mais localizados no âmbito do surto (por exemplo, uma cidade pode ser mais afetada que outra, ou haver focos diferentes dentro da mesma cidade).

Para além disso, estes modelos precisam de ser ajustados aos dados existentes, o que faz com que quanto mais complexo for o modelo maior as incertezas no ajuste. Isto pode levar a enormes sub ou sobrestimativas dos números da epidemia.

Para contornar estes problemas, existem modelos estocásticos para a modelação de epidemias, muitos baseados em Cadeias Markovianas e métodos de Monte Carlo¹¹.

Conclusões

Os modelos compartimentais são modelos matemáticos versáteis e de relativa simplicidade que permitem compreender de forma expedita a evolução temporal de uma série de conceitos de aplicação em inúmeras áreas do conhecimento, como as ciências biomédicas, a epidemiologia, a dinâmica das populações, e a informática. No caso da pandemia causada pelo vírus infecioso SARS-CoV-2, não deixa de ser interessante verificar que os modelos compartimentais vêm ao auxílio de duas ciências fundamentais para o combate a esta epidemia: a farmacocinética, e os modelos epidémicos. É por vezes difícil encontrar bibliografia sobre os fundamentos matemáticos e científicos por trás destes modelos. Neste artigo procuramos dar uma visão geral do que são estes modelos, e das diversas áreas de aplicação, apesar de termos plena consciência que o leque de aplicações não se reduz ao que aqui foi exposto.